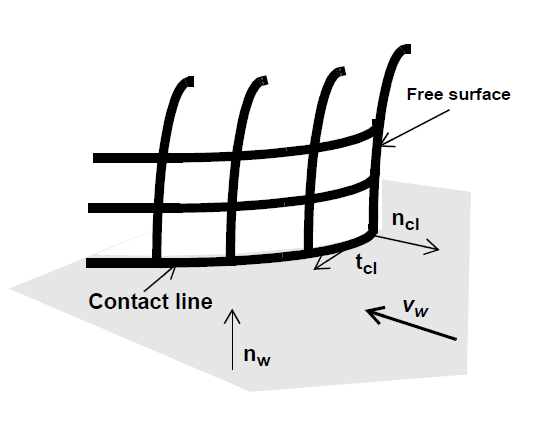
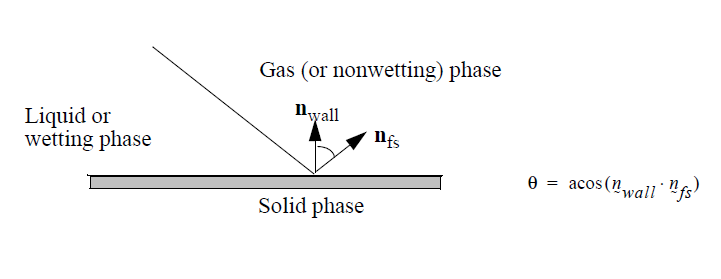
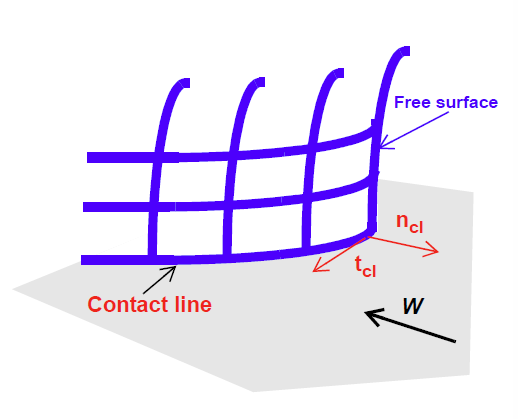
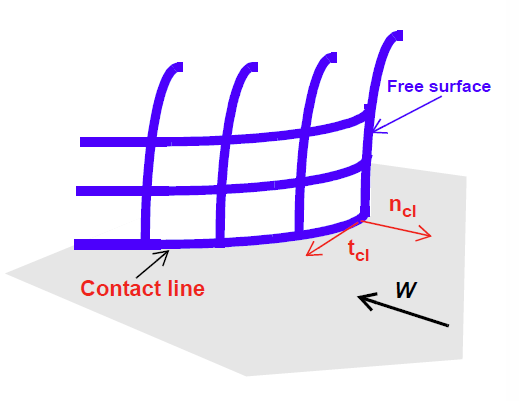
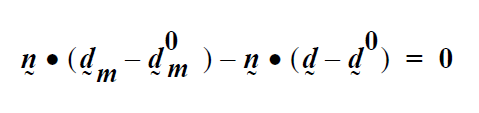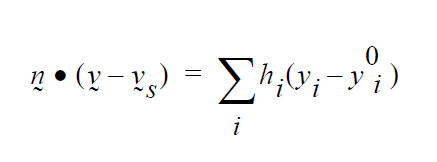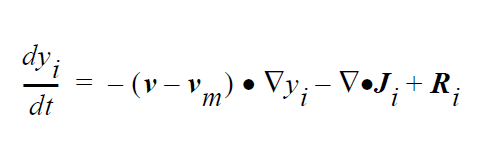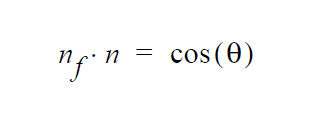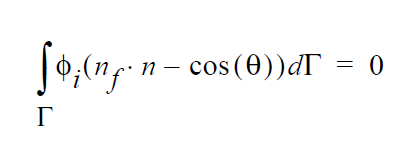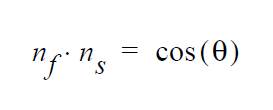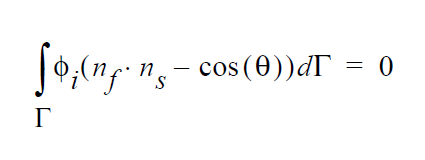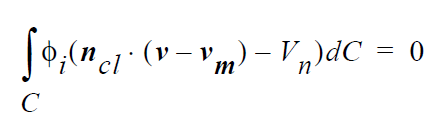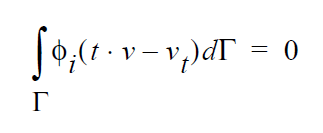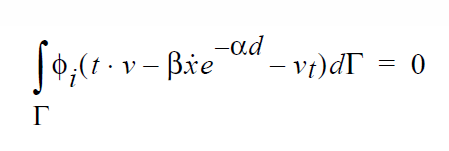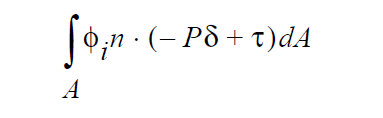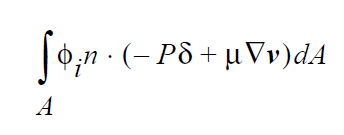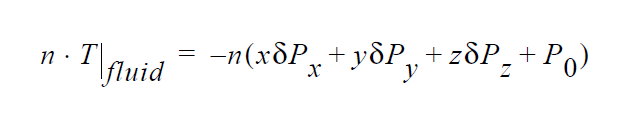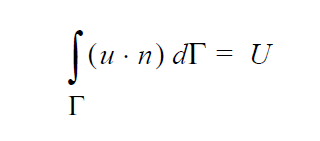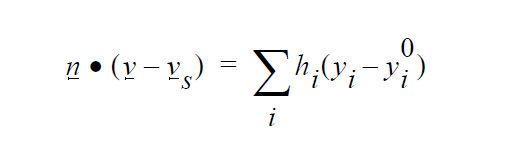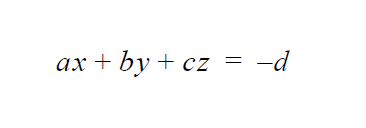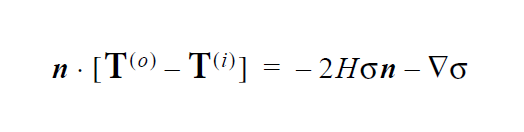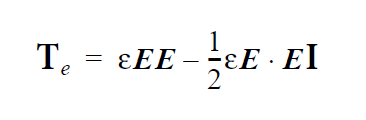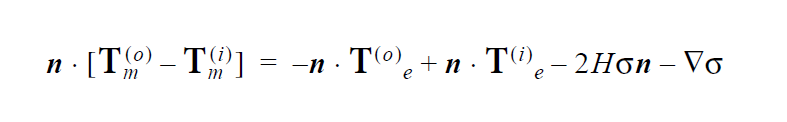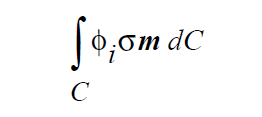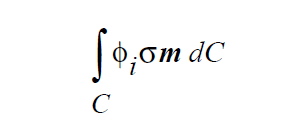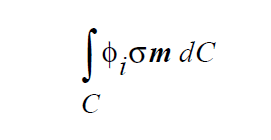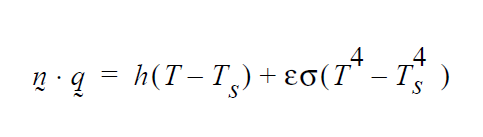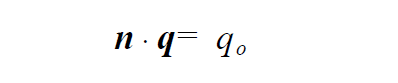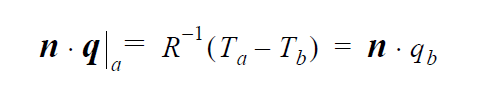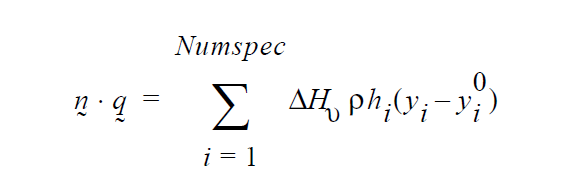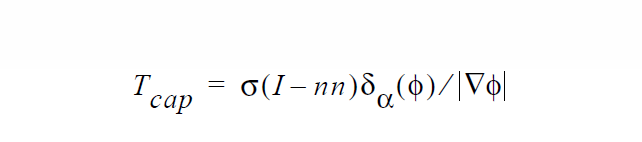Boundary Condition Specifications¶

The broad range of mechanics capabilities that has been built into Goma necessitates an equally broad range of boundary conditions (BCs) to provide all boundary condition information that the differential equations specified in the Problem Description section will require for a well-posed system. The BCs for Goma have been categorized according to the differential equation set to which they apply. First are listed those boundary conditions which can be applied to any equation followed by BCs for mesh, real solid, fluid momentum, energy, mass, continuity, porous, stress, gradient, shear rate, fill and potential equations. Each boundary condition (BC) card follows a general syntax as follows:

BC = <bc_name> <bc_type> <bc_id> {integer_list}/{float_list}

The <bc_name> identifies the desired control of the physics/mechanics at the boundary as identified by the <bc_type> and its associated <bc_id>. The <bc_type> is either nodeset, NS (NODEBC or POINBC in EXODUS II) or sideset, SS (ELEMBC in EXODUS II) depending on the <bc_name> and can be located in the problem domain by means of its flag or <bc_id> number (set in EXODUS II). The {integer_list} and/or {float_list} specify parameters of the boundary condition. Within each equation category are Dirichlet nodeset boundary conditions (i.e. T, U, V, W, DX, DY, DZ, Y, S11, S12, S13, S22, S23, S33, G11, G12, G13, G21, G22, G23, G31, G32, G33) that can be handled (i.e., processed) in two ways in Goma. The first way is application of the BC as a “hard-set” on the primitive variable, and the second as a residual equation; differences in these methods are discussed below. The cards belonging to this category have the following general syntax:

BC = <bc_name> <bc_type> <bc_id> <float1> <float2>

where <float2> flags whether a hard-set or residual equation is to be used.

Prior to introducing individual boundary conditions and their parameters, some general comments regarding the first category of BCs, boundary condition types and the resolution of boundary condition conflicts will be made.

Any Equation Boundary Conditions - There are several boundary condition types that are not necessarily best binned with a specific equation type. The FIX, GD_* and TABLE boundary condition types are general and can be applied to any equation type. A general description of these types (called Category 1) is given below.

Boundary Condition Types - Beyond the generalized boundary conditions types and the Dirichlet types, Goma has strong-collocated, weak form, and several others that are intrinsic to the Galerkin finite element method; these are applied in a variety of ways. Because of this, boundary conditions at a given node might interact in ways that produce unexpected results. For this reason, it is important to understand the differing methods of application that occur in Goma and how each affects the other. In addition, by cleverly mixing boundary conditions, the analyst is often able to achieve a desired result, but only if the nature of each boundary condition is understood. Toward this end, the user will find a special label assigned to each boundary condition, which, with the ensuing explanation below, will provide each user with an understanding of how that BC is applied within Goma.

On each boundary condition card, the boundary condition type appears in the Description/Usage section. These are the following boundary condition types that will be found here:

DIRICHLET (DC)
STRONGLY INTEGRATED (SIC)
STRONGLY INTEGRATED EDGE (SIC_EDGE)
COLLOCATED (PCC)
COLLOCATED EDGE (PCC_EDGE)
WEAKLY INTEGRATED (WIC)

The following sections discuss the method of application of each boundary condition type along with the implications of using each.

DIRICHLET (DC):

In the hierarchy of boundary conditions, Dirichlet conditions are at the top. Nothing trumps a Dirichlet conditions. A Dirichlet condition is applied by discarding all mechanics information related to a particular field variable that has been accumulated at a given node and replacing it with a direct assignment of the nodal unknown of that field with a fixed a priori value. Algorithmically, applying a Dirichlet condition on a degree of freedom at a node involves zeroing the entire equation row, inserting a unity value on the diagonal element of the Jacobian matrix, inserting a zero value at the appropriate place in the residual vector, and inserting the known boundary condition value at the appropriate place in the solution vector. This is referred to in many places as the “hard set” method. An alternate formulation imposes the boundary condition by replacing the mechanics equation at a node with the simple residual equation, EQUATION , where φ and φ0 are the nodal unknown field and its assigned value, respectively.The sensitivities of this residual equation are entered into the Jacobian appropriately and solution takes place normally.

Dirichlet conditions are strictly node-based. Neighbor nodes and shared elements have no influence on them. For this reason, all Dirichlet conditions are applied to nodesets. Furthermore, Dirichlet conditions are assigned the highest precedence in terms of boundary conditions. If a Dirichlet condition appears at a node, it will be applied. Any other boundary condition that could be applied will be discarded (at that node).

Dirichlet conditions are limited, however in that they can only affect the nodal value of a degree of freedom. Derived quantities cannot be set with a Dirichlet condition. You will never see a Dirichlet condition being applied to a heat flux for example.

STRONGLY INTEGRATED (SIC):

The next class of boundary condition is referred to within Goma as the strongly integrated boundary conditions. These boundary conditions replace the mechanics equation at the i^th node with a surface integral of some derived quantity. The general form of these conditions is:

\[\int_{S} \phi_i \, g(\mathbf{x}) \, \mathrm{d}S = 0\]

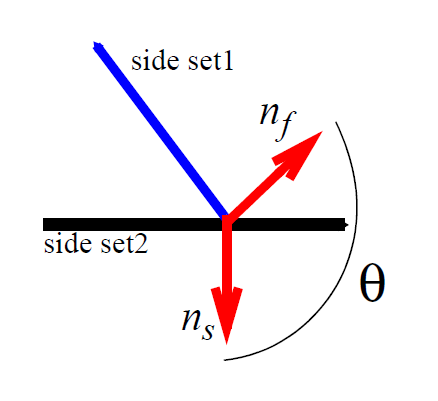
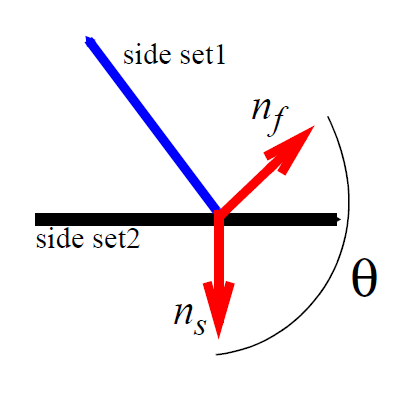
where in this case \(g(\mathbf{x})\) is not a residual equation but some derived quantity. Unlike strong constraints, this term is not multiplied by a penalizing factor before it is added to the accumulated mechanics equation at node i. Consequently, it represents boundary contributions to the mechanics at that node. Note also that since these conditions only make additions to the boundary mechanics, if a strongly enforced condition (SIC or PCC) is also present at the node, the weakly integrated constraint will be clobbered along with the rest of the mechanics. As an example, a CAPILLARY boundary condition that is applied to the same sideset as a VELO_NORMAL condition will have no effect in the final answer.

Weakly integrated boundary conditions are also very much a consequence of the “natural” boundary conditions that emerge from the finite element formulation. As anyone familiar with the finite element method knows, these are the ghostly boundary terms that enforce zero boundary fluxes or forces as a convenient default. The weakly integrated boundary condition step into the space afforded by the natural boundary conditions and allow the user to specify values for these boundary fluxes or forces as functions of conditions on those boundaries.

In addition, to the various classes of boundary conditions detailed above, there are special cases that arise when applying boundary conditions to the “vector” degrees of freedom. Currently, the only “vector” degrees of freedom are the mesh displacement and fluid velocity unknowns. When a boundary condition is applied to these degrees of freedom, it may be ROTATED, VECTOR or SCALAR. These labels appear in the boundary condition documentation along with the class of the condition.

ROTATED:

When a boundary condition is designated as “ROTATED,” the vector components of the appropriate equations for the surface nodes are projected into a new coordinate system that is locally based on the surface normal vector and tangent vectors. It is the presence of the “ROTATED” boundary condition that prompts this process. Usually, only one of these rotated components is then affected by the boundary condition constraint and in this sense ROTATED conditions are SCALAR conditions (see below). Also generally speaking, ROTATED boundary conditions are strongly enforced as described above.

VECTOR:

When a boundary condition is designated as a “VECTOR” condition, the implication is that a vector quantity will be added to the vector components of the original mechanics equations. “VECTOR” boundary conditions are generally always applied weakly.

SCALAR:

When a boundary condition is designated a “SCALAR” condition, only a single mechanics equation is going to be influenced by the boundary condition. In the case of the vector degrees of freedom, only a single component would be affected by the boundary condition. Boundary conditions that apply to degrees of freedom that are naturally scalars, for instance temperature and species, are by default SCALAR conditions.

An example of these special labels for the VELO_NORMAL_EDGE condition (found on the line with the Description/Usage section header) is PCC-EDGE/ROTATED MOMENTUM indicating a rotated collocated edge condition applied to the fluid momentum equation. Given this labeling convention, boundary conditions which are not specified to be rotated or vector conditions can be presumed to be unrotated scalar conditions. Boundary conditions that may be applied to any equation are labeled “varied.”

The user will not find “periodic boundary conditions” discussed in this manual. Those interested in such conditions should consult the Advanced Capabilities Manual (SAND2006-7304).

Resolving Conflicts between Boundary Conditions - In Goma, the bulk equations and boundary conditions are evaluated on an element-by-element basis. After the residual and Jacobian entries for the bulk equations have been calculated, the boundary conditions are used to modify or replace the bulk entries where necessary. Often the selection of boundary conditions from the input deck may cause two boundary conditions to be applied to the same equation (equation associated with a nodal point); this is especially true at junction points. Frequently the multiple boundary conditions perform the same function (i.e. duplicates) but in some important instances they are different (i.e. conflicts). In Goma, a decision making process was developed for determining which boundary conditions have priority. The flow chart for this decision-making is shown in Figure 4. While this process resolves boundary-condition conflicts, it does not eliminate the possibility of setting boundary conditions that are incompatible and lead to errors in solving the problem. However, this method should clarify how BC’s are chosen from the input deck and should enable the user to determine why a given combination of boundary conditions does not work.

The flow chart in Figure 3 shows the procedure for resolving what boundary conditions get applied to a given equation at a given node. The starting point assumes that a list of all the potential boundary conditions for the equation are known. Boundary conditions in Goma fall into several classes: Dirichlet, Pointwise Collocation, Strong Integrated, Weak Integrated and Special conditions, in order of priority. For boundary conditions applied to vector equations (mesh or momentum), a boundary condition can cause the bulk equations to be rotated prior to applying the boundary condition; in conflicts between boundary conditions, conditions which do not rotate the bulk equations (unrotated conditions) have priority over conditions which rotate the bulk equations (rotated conditions). In certain cases (e.g. two PLANE conditions which intersect at a point), conflicting boundary conditions can be checked to determine if they are duplicates, in which case only the first of the duplicates in the input deck is applied. Most boundary conditions are designed to apply by themselves, but a special class of boundary conditions, the generalized dirichlet (GD) conditions, are designed so that multiple GD conditions can apply along the same boundary and to the same equation.

While running, Goma prints the results of conflict resolution for every node at which it found at least two boundary conditions being applied to the same equation. The results indicate the node number, equation type, boundary conditions chosen by Goma, and the side-set or node-set numbers to which the boundary conditions apply. Thus to determine what boundary conditions are actually used by Goma, carefully check the output from conflict resolution. Setting the Debug_Flag = 1 causes Goma to print out more information regarding which boundary conditions apply and which do not. Despite the complexity of the logic built into Goma to resolve conflicts between boundary conditions, there are several combinations of boundary conditions that do not have a clear resolution. It is up to the user to resolve the final conflicts.

And finally, the first (Number of BC) and last (END OF BC) boundary condition cards are a pair and stand alone; the remaining cards belong to the categories of conditions discussed above. The ordering of input cards within this collection of BC input records (i.e., section) is sequential and some sections of interspersed comments accompany each boundary condition category.

Number of BC¶

Number of BC = <integer>

Description / Usage¶

This required card indicates how many boundary condition (BC) cards are contained in the Problem Description File. The single input parameter is defined as

<integer>: The number of BC cards that follow.

If <integer> is set to -1, Goma will automatically count the number of BC cards between the Number of BC card and the End of BC card. This latter usage is generally preferred if a large number of BCs are to be specified.

Examples¶

Following is a sample card, indicating that there are two BC cards that follow this card.

Number of BC = 2

Technical Discussion¶

If there are more BC cards listed in an input deck than specified on this card, Goma ignores the extras; in other words, only the first <integer> cards are read by Goma. If the number of BCs is fewer than the amount specified by <integer>, Goma will stop with an error.

Also note, that if more than one BC on the same variable is specified, only the last one is applied.

Category 1: Any Equation¶

This category includes a set of cards that are used to provide all boundary condition information for a generalized dirichlet (GD) boundary condition. The condition is applied as a pointwise collocation along a given node set. The general syntax for the GD_cards is as follows:

BC = <bc_name> <bc_type> <bc_id> <equation_name> <integer1> <variable_name> <integer2> {float_list}

The current allowable definitions and/or values for < bc_name>, <bc_type>, <bc_id>, <integer1>, <integer2> and {float_list} are provided in the individual cards. As a general note, <integer1> and <integer2> are the species number of the mass transport equation and concentration variable, respectively; they should be zero for other equation and variable types. Currently these conditions assume that the variable is defined at all the nodes at which the equation is defined (no subparametric mapping).

However, the values for <equation_name> and <variable_name>, which apply generally to all cards in this category (except as subsequently noted), are given here:

<equation_name>

A character string indicating the equation to which this boundary condition is applied, which can be

R_MOMENTUM1 R_MOMENTUM2 R_MOMENTUM3
R_MESH1 R_MESH2 R_MESH3
R_MASS R_ENERGY R_MASS_SURF
R_PRESSURE
R_STRESS11 R_STRESS12 R_STRESS13
R_STRESS22 R_STRESS23 R_STRESS33
R_GRADIENT11 R_GRADIENT12
R_GRADIENT13 R_GRADIENT21
R_GRADIENT22 R_GRADIENT23
R_GRADIENT31 R_GRADIENT32
R_GRADIENT33 R_POTENTIAL R_FILL
R_SHEAR_RATE R_MESH_NORMAL (rotate mesh equations and apply this condition to normal component)
R_MESH_TANG1 R_MESH_TANG2
R_MOM_NORMAL (rotate momentum equations and apply this condition to normal component)
R_MOM_TANG1 R_MOM_TANG2
R_POR_LIQ_PRESS R_POR_GAS_PRESS
R_POR_POROSITY R_POR_SATURATION
R_POR_ENERGY R_POR_LAST
R_POR_SINK_MASS R_VORT_DIR1
R_VORT_DIR2 R_VORT_DIR3 R_VORT_LAMBDA
R_CURVATURE R_LAGR_MULT1
R_LAGR_MULT2 R_LAGR_MULT3
R_BOND_EVOLUTION R_SURF_CHARGE
R_EXT_VELOCITY R_EFIELD1 R_EFIELD2
R_EFIELD3 R_ENORM R_NORMAL1
R_NORMAL2 R_NORMAL3 R_ _CURVATURE
R_SHELL_TENSION R_SHELL_X R_SHELL_Y
R_SHELL_USER R_PHASE1 R_PHASE2
R_PHASE3 R_PHASE4 R_PHASE5
R_SHELL_ANGLE1 R_SHELL_ANGLE2
R_SHELL_SURF_DIV_V R_SHELL_SURF_CURV
R_N_DOT_CURL_V R_GRAD_S_V_DOT_N1
R_GRAD_S_V_DOT_N2 R_GRAD_S_V_DOT_N3
R_ACOUS_PREAL R_ACOUS_PIMAG
R_SHELL_DIFF_FLUX
R_SHELL_DIFF_CURVATURE
R_SHELL_NORMAL1 R_SHELL_NORMAL2
R_ACOUS_REYN_STRESS R_SHELL_BDYVELO
R_SHELL_LUBP R_LUBP R_SHELL_FILMP
R_SHELL_FILMH R_SHELL_PARTC
R_SHELL_SAT_CLOSED R_SHELL_SAT_OPEN
R_SHELL_ENERGY R_SHELL_DELTAH
R_SHELL_LUB_CURV R_SHELL_SAT_GASN
R_SHELL_SHEAR_TOP R_SHELL_SHEAR_BOT
R_SHELL_CROSS_SHEAR R_MAX_STRAIN
R_CUR_STRAIN R_LUBP_2
R_SHELL_SAT_OPEN_2 or
R_SHELL_LUB_CURV_2

<variable_name>

A character string indicating the variable which should be fixed, which can be

VELOCITY1 VELOCITY2 VELOCITY3
MESH_DISPLACEMENT1
MESH_DISPLACEMENT2
MESH_DISPLACEMENT3 MESH_POSITION1
MESH_POSITION2 MESH_POSITION3
MASS_FRACTION SURFACE TEMPERATURE or
PRESSURE (pressure will have no effect if not using Q1 or Q2 basis functions)
POLYMER_STRESS11
POLYMER_STRESS12 POLYMER_STRESS13
POLYMER_STRESS22 POLYMER_STRESS23
POLYMER_STRESS33 VOLTAGE FILL
SHEAR_RATE VEL_NORM D_VEL1_DT
D_VEL2_DT D_VEL3_DT D_T_DT D_C_DT
D_X1_DT D_X2_DT D_X3_DT D_S_DT D_P_DT
VELOCITY_GRADIENT11
VELOCITY_GRADIENT12
VELOCITY_GRADIENT13
VELOCITY_GRADIENT21
VELOCITY_GRADIENT22
VELOCITY_GRADIENT23
VELOCITY_GRADIENT31
VELOCITY_GRADIENT32
VELOCITY_GRADIENT33 POR_LIQ_PRESS
POR_GAS_PRESS POR_POROSITY
POR_POROSITY POR_TEMP POR_SATURATION
POR_LAST MAX_POROUS_NUM
POR_SINK_MASS VORT_DIR1 VORT_DIR2
VORT_DIR3 VORT_LAMBDA CURVATURE
LAGR_MULT1 LAGR_MULT2 LAGR_MULT3
BOND_EVOLUTION SURF_CHARGE
EXT_VELOCITY EFIELD1 EFIELD2 EFIELD3
ENORM NORMAL1 NORMAL2 NORMAL3
SHELL_CURVATURE SHELL_TENSION
SHELL_X SHELL_Y SHELL_USER PHASE1
PHASE2 PHASE3 PHASE4 PHASE5
SHELL_ANGLE1 SHELL_ANGLE2
SHELL_SURF_DIV_V SHELL_SURF_CURV
N_DOT_CURL_V GRAD_S_V_DOT_N1
GRAD_S_V_DOT_N2 GRAD_S_V_DOT_N3
ACOUS_PREAL ACOUS_PIMAG
SHELL_DIFF_FLUX SHELL_DIFF_CURVATURE
SHELL_NORMAL1 SHELL_NORMAL2
ACOUS_REYN_STRESS SHELL_BDYVELO
SHELL_LUBP LUBP SHELL_FILMP
SHELL_FILMH SHELL_PARTC
SHELL_SAT_CLOSED SHELL_PRESS_OPEN
SHELL_TEMPERATURE SHELL_DELTAH
SHELL_LUB_CURV SHELL_SAT_GASN
SHELL_SHEAR_TOP SHELL_SHEAR_BOT
SHELL_CROSS_SHEAR MAX_STRAIN
CUR_STRAIN LUBP_2 SHELL_PRESS_OPEN2
SHELL_LUB_CURV_2

EXCEPTIONS to the above parameter definitions: For the GD_TIME card, the <variable_names> of LINEAR, EXPONENTIAL, or SINUSOIDAL are acceptable (see examples below). There are also differences in the use of the GD_TABLE card, which are explained in the description of that card below.

A GD boundary condition can be applied multiple times to the same side set and equation to build up a general multiparameter condition. When this is done, the function is built by expanding the equations sequentially in the order specified in the BC list.

Descriptions of the GD cards are given next. An insert entitled “Usage Notes on the GD Cards” follows the descriptions, explaining how the cards are used together in various combinations.

FIX¶

BC = FIX NS <bc_id> {char_string} <integer1>

Description / Usage¶

(DC/VARIED)

This boundary condition card is used to fix the value of a nodal variable along a node set to the value it receives from an initial guess file (viz. either from the neutral file specified by the Initial Guess card or an input EXODUS II file as also specified by the read_exoII_file option on the Initial Guess card). The boundary condition is applied as a Dirichlet condition (see technical discussion below).

Definitions of the input parameters are as follows:

FIX

Name of the boundary condition (<bc_name>).

NS

Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.

<bc_id>

The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.

{char_string}

Variable name that is to be fixed. This parameter can have the following permissible values:

VELOCITY1
VELOCITY2 VELOCITY3
MESH_DISPLACEMENT1
MESH_DISPLACEMENT2
MESH_DISPLACEMENT3
SOLID_DISPLACEMENT1
SOLID_DISPLACEMENT2
SOLID_DISPLACEMENT3 MASS_FRACTION
TEMPERATURE PRESSURE VOLTAGE FILL
POLYMER_STRESS11 POLYMER_STRESS12
POLYMER_STRESS13 POLYMER_STRESS22
POLYMER_STRESS23 POLYMER_STRESS33
VELOCITY_GRADIENT11
VELOCITY_GRADIENT12
VELOCITY_GRADIENT13
VELOCITY_GRADIENT21
VELOCITY_GRADIENT22
VELOCITY_GRADIENT23
VELOCITY_GRADIENT31
VELOCITY_GRADIENT32
VELOCITY_GRADIENT33 POR_LIQ_PRES
POR_GAS_PRES POR_POROSITY
POR_POROSITY POR_TEMP POR_SATURATION
POR_LAST MAX_POROUS_NUM
POR_SINK_MASS VORT_DIR1 VORT_DIR2
VORT_DIR3 VORT_LAMBDA CURVATURE
LAGR_MULT1 LAGR_MULT2 LAGR_MULT3
BOND_EVOLUTION SURF_CHARGE
EXT_VELOCITY EFIELD1 EFIELD2 EFIELD3
ENORM NORMAL1 NORMAL2 NORMAL3
SHELL_CURVATURE SHELL_TENSION
SHELL_X SHELL_Y SHELL_USER PHASE1
PHASE2 PHASE3 PHASE4 PHASE5
SHELL_ANGLE1 SHELL_ANGLE2
SHELL_SURF_DIV_V SHELL_SURF_CURV
N_DOT_CURL_V GRAD_S_V_DOT_N1
GRAD_S_V_DOT_N2 GRAD_S_V_DOT_N3
ACOUS_PREAL ACOUS_PIMAG
SHELL_DIFF_FLUX SHELL_DIFF_CURVATURE
SHELL_NORMAL1 SHELL_NORMAL2
ACOUS_REYN_STRESS SHELL_BDYVELO
SHELL_LUBP LUBP SHELL_FILMP
SHELL_FILMH SHELL_PARTC
SHELL_SAT_CLOSED SHELL_PRESS_OPEN
SHELL_TEMPERATURE SHELL_DELTAH
SHELL_LUB_CURV SHELL_SAT_GASN
SHELL_SHEAR_TOP SHELL_SHEAR_BOT
SHELL_CROSS_SHEAR MAX_STRAIN
CUR_STRAIN LUBP_2 SHELL_PRESS_OPEN2
SHELL_LUB_CURV_2

<integer1>

Species number of concentration, or zero if variable is not concentration.

Examples¶

The following is an example of using this card to set the mesh displacement components in a 2-D problem:

BC =    FIX    NS    4    MESH_DISPLACEMENT1    0

BC =    FIX    NS    4    MESH_DISPLACEMENT2    0

In this example, several continuation steps were taken to deform part of an elastic block of material. The displacements on boundary node set 4 were then held constant while moving another boundary (because the current displacements were not known, FIX was a convenient tool).

Technical Discussion¶

This boundary condition capability is indispensable for moving-mesh problems when the dependent variable is the mesh displacement from a stress free state. If one were to try to use the DX/DY/DZ type Dirichlet condition to suddenly freeze a mesh along a node set after a parameter continuation or transient problem restart, then they would be faced with figuring out the displacement of each node and defining individual node sets for each node for boundary condition application. This capability is also beneficial when using previous simulation results to generate boundary conditions for more complex analysis. We have on occasion used this boundary condition for most of the variable types shown.

GD_CONST¶

BC = GD_CONST SS <bc_id> <equation_name> <integer1> <variable_name> <integer2> <float>

Description / Usage¶

(PCC/VARIED)

This boundary condition of type Category 1 (see discussion) is used to impose a constant value for any nodal variable, using the residual function form

\[x - C_1 = 0\]

\(C_1\) being the constant value (<float>) and \(x\) being the <variable_name>. This boundary condition card can be used in combination with any of the other GD_* conditions as a building block to construct more complicated conditions. Please see the examples on all of these cards for details and instructive uses. Definitions of the input parameters are as follows:

GD_CONST: Name of the boundary condition (<bc_name>).
SS: Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>: The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<equation_name>: A character string indicating the equation to which this boundary condition is applied (see the list of permissible values in the discussion above for Category 1).
<integer1>: Species number of the mass transport equation. The value should be 0 unless the <equation_name> is of type R_MASS.
<variable_name>: A character string indicating the variable that should be fixed (see the list of permissible values in the discussion above for Category 1).
<integer2>: Species number of the concentration variable.The value should be 0 unless the <variable_name> is of type MASS_FRACTION.
<float>: Value of variable \(C_1\).

Examples¶

Following is a sample card:

BC = GD_CONST SS 2 R_MESH_NORMAL 0 MASS_FRACTION 0 0.2

This boundary condition results in the equation \(C_1 - 0.2 = 0\) being applied as a boundary condition to the mesh-motion equation and being rotated into a normal-tangential basis. \(C_1\) is the concentration of the zeroth species. The equation is actually applied as a replacement to the normal component of the mesh motion equation and in this case would cause the mesh surface, defined by side set 2, to move as the isoconcentration surface of \(C_1 = 0.2\).

Technical Discussion¶

Note that this collocated boundary condition may be applied as a rotated, vector or scalar condition depending on the equation to which this condition applies. The example above is a powerful demonstration of this boundary condition as a distinguishing condition. Please consult the example discussions on the other GD_* options for more detailed examples, as this boundary condition card can be used in an additive way with other GD_* cards.

GD_LINEAR¶

BC = GD_LINEAR SS <bc_id> <equation_name> <integer1> <variable_name> <integer2> <float1> <float2>

Description / Usage¶

(PCC/VARIED)

This boundary condition of type Category 1 (see discussion) is used to impose a linear function for any nodal variable, using the residual function form

\[C_1 + C_2x = 0\]

where \(C_1\) and \(C_2\) being the constant values and \(x\) representing any variable (<variable_name>). This boundary condition card can be used in combination with any of the other GD_* conditions as a building block to construct more complicated conditions. Moreover, the resulting boundary condition can be applied as a strong residual replacement to any differential equation type. Please see the examples on all of these cards for details and instructive uses. Definitions of the input parameters are as follows:

GD_LINEAR: Name of the boundary condition (<bc_name>).
SS: Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>: The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<equation_name>: A character string indicating the equation to which this boundary condition is applied (see the list of permissible values in the discussion above for Category 1).
<integer1>: Species number of the mass transport equation. The value should be 0 unless the <equation_name> is of type R_MASS.
<variable_name>: A character string indicating the variable that should be fixed (see the list of permissible values in the discussion above for Category 1).
<integer2>: Species number of the concentration variable.The value should be 0 unless the <variable_name> is of type MASS_FRACTION.
<float1>: Intercept \(C_1\)
<float2>: Slope \(C_2\)

Examples¶

Following is a sample card:

BC = GD_LINEAR SS 1 R_MESH1 0 MESH_POSITION1 0 -1. 2.

This boundary condition results in the equation \(2.0*x - 1.0 = 0\) to be applied as a boundary condition to the x-component of the mesh motion equation. x is the xcomponent of the mesh position (N.B. not displacement, as MESH_POSITION1 would be replaced by MESH_DISPLACEMENT1 in the above). The equation is actually applied as a replacement to the x-component of the mesh motion equation and in this case would lead to the mesh surface, defined by side set 1, to move or position itself according to this linear relationship.

Technical Discussion¶

Note that this collocated boundary condition may be applied as a rotated, vector or scalar condition depending on the equation to which this condition applies. Please consult the example discussions on the other GD_* options for more detailed examples, as this boundary condition card can be used in an additive way with those.

GD_PARAB¶

BC = GD_PARAB SS <bc_id> <equation_name> <integer1> <variable_name> <integer2> <float1> <float2> <float3>

Description / Usage¶

(PCC/VARIED)

This boundary condition of type Category 1 (see discussion) is used to impose a quadratic function for any nodal variable, using the residual function form

\[C_1 + C_2x + C_3x^2 = 0\]

where \(C_1\), \(C_2\), and \(C_3\) are the constant values (<float>) and \(x\) represents any variable (<variable_name>). This boundary condition card can be used in combination with any of the other GD_* conditions as a building block to construct more complicated conditions. Moreover, the resulting boundary condition can be applied as a strong residual replacement to any differential equation type. Please see the examples on all of these cards for details and instructive uses. Definitions of the input parameters are as follows:

GD_PARAB: Name of the boundary condition (<bc_name>).
SS: Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>: The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<equation_name>: A character string indicating the equation to which this boundary condition is applied (see the list of permissible values in the discussion above for Category 1).
<integer1>: Species number of the mass transport equation. The value should be 0 unless the <equation_name> is of type R_MASS.
<variable_name>: A character string indicating the variable that should be used in the function (see the list of permissible values in the discussion above for Category 1).
<integer2>: Species number of the concentration variable.The value should be 0 unless the <variable_name> is of type MASS_FRACTION.
<float1>: Intercept \(C_1\).
<float2>: Slope \(C_2\).
<float3>: Acceleration \(C_3\).

Examples¶

Following is a sample card:

BC = GD_PARAB SS 4 R_MESH1 0 MESH_POSITION2 0 1. -2. -3.

BC = GD_LINEAR SS 4 R_MESH1 0 MESH_DISPLACEMENT1 0   0. -1.

This boundary condition results in the equation \(-3*y^2-2.0*y + 1.0 = 0\) to be applied as a boundary condition to the x-component of the mesh motion equation. y is the ycomponent of the mesh position (N.B. not displacement, as MESH_POSITION2 would be replaced by MESH_DISPLACEMENT2 in the above). The equation is actually applied as a replacement to the x-component of the mesh motion equation and in this case would lead to the mesh surface, defined by side set 4, to move or position itself according to this quadratic relationship.

Technical Discussion¶

This condition is convenient for applying Poiseuille velocity profiles, as a circular condition on geometry, together with many other uses.

Note that this collocated boundary condition may be applied as a rotated, vector or scalar condition depending on the equation to which this condition applies. Please consult the example discussions on the other GD_* options and the examples below for more detailed examples, as this boundary condition card can be used in an additive way with those.

References¶

Please consult the following reference (on Roll Coating) for examples of roll surface geometry.

GT-003.1: Roll coating templates and tutorial for GOMA and SEAMS, February 29, 2000, P. R. Schunk and Matt Stay

GD_POLYN¶

BC = GD_POLYN SS <bc_id> <equation_name> <integer1> <variable_name> <integer2> <float_list>

Description / Usage¶

(PCC/VARIED)

This boundary condition of type Category 1 (see discussion) is used to impose a polynomial function for any nodal variable, using the residual function form of a 6^th order polynomial dependence on a variable

\[C_1 + C_2x + C_3x^2 + C_4x^3 + C_5x^4 + C_6x^5 + C_7x^6 = 0\]

There are three required and four optional parameters in the <float_list>; definitions of the input parameters are as follows:

GD_POLYN: Name of the boundary condition (<bc_name>).
SS: Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>: The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<equation_name>: A character string indicating the equation to which this boundary condition is applied (see the list of permissible values in the discussion above for Category 1).
<integer1>: Species number of the mass transport equation. The value should be 0 unless the <equation_name> is of type R_MASS.
<variable_name>: A character string indicating the variable that should be fixed (see the list of permissible values in the discussion above for Category 1).
<integer2>: Species number of the concentration variable. The value should be 0 unless the <variable_name> is of type MASS_FRACTION.
<float1>: Intercept \(C_1\).
<float2>: Slope \(C_2\).
<float3>: Acceleration \(C_3\).
<float4>: Coefficient for 3rd-order term \(C_4\).
<float5>: Coefficient for 4th-order term \(C_5\).
<float6>: Coefficient for 5th-order term \(C_6\).
<float7>: Coefficient for 6th-order term \(C_7\).

Examples¶

Following is a set of sample cards:

BC = GD_POLYN SS 2 R_ENERGY 0 MESH_POSITION1 0 {c1} {c2} {c3} {c4} {c5} {c6} {c7}

BC = GD_LINEAR SS 2 R_ENERGY 0 TEMPERATURE 0   0. -1.

This boundary condition results in the equation

\[C_1 + C_2x + C_3x^2 + C_4x^3 + C_5x^4 + C_6x^5 + C_7x^6 = T\]

to be applied as a boundary condition on the energy equation, i.e., made a boundary condition on temperature with second card, which brings in a dependence on temperature. Here the coefficients are set by APREPRO, \(x\) is the x-component of the mesh position (N.B. not displacement, as MESH_POSITION2 would be replaced by MESH_DISPLACEMENT2 in the above).

Technical Discussion¶

This condition is not used as often as GD_LINEAR and GD_PARAB, and in fact supersedes those conditions. Please consult the example discussions on the other GD_* options and the example section after GD_TABLE for more descriptive examples.

GD_TIME¶

BC = BC = GD_TIME SS <bc_id> <equation_name> <integer1> <time_func_name> <integer2> <float1> <float2> [float3]

Description / Usage¶

(PCC/VARIED)

This boundary condition card is actually a multiplicative building block that can be used to impose a multiplicative time modulation of a specified functional form on any set of GD_* conditions. NOTE: unlike the other GD_* cards which are additive, this card is multiplicative. This condition must be placed after any single or set of GD_* cards for which the user wishes to modulate (viz. GD_LINEAR, GD_PARAB, etc.). The card can be used as many times as needed to construct the desired function. The examples below will clarify its use. Definitions of the input parameters are as follows:

GD_TIME: Name of the boundary condition (<bc_name>).
SS: Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>: The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<equation_name>: A character string indicating the equation to which this boundary condition is applied (see the list of permissible values in the discussion above for Category 1).
<integer1>: Species number of the mass transport equation. The value should be 0 unless the <equation_name> is of type R_MASS.
<time_func_name>: Keyword to identify the functional form of the time modulation. Permissible values for this parameter are LINEAR, EXPONENTIAL, and SINUSOIDAL.
<integer2>: Set this required but unused parameter to zero.
<float1>: \(C_0\) model parameter
<float2>: \(C_1\) model parameter
[float3]: Optional parameter to add a maximum time to be applied if \(t > t_{max}\) then \(t\) is set to \(t_{max}\)

The functional form of each time-modulation model is as follows:

LINEAR:	\(f(t) = C_0 + C_1t\)
EXPONENTIAL:	\(f(t) = \exp \left(C_0 + C_1t \right)\)
SINUSOIDAL:	\(f(t) = \sin \left(C_0 + C_1t \right)\)

Examples¶

Following is a sample card set:

BC = GD_LINEAR SS 1 R_MESH_NORMAL 0 MESH_DISPLACEMENT1 0 1. 0.
BC = GD_TIME SS 1 R_MESH_NORMAL 0 SINUSOIDAL 0 10. 2.
BC = GD_LINEAR SS 1 R_MESH_NORMAL 0 MESH_POSITION1 0 0. -1.

This set of cards leads to the application of \(x = sin(10.0 + 2t)\) to the normal component of the mesh displacement at side set 1. If side set 1 were a surface of constant x (viz. normal in the x-direction) then this condition could be used to impose a piston motion to the surface. Recall that GD_LINEAR cards are additive with each other and GD_TIME is multiplicative with the previous cards. The first card is used to put a constant of 1.0 in the equation, the second card (GD_TIME card) multiplies that constant with the sinusoidal time function, and the third card is used to put the linear term on mesh position. Note carefully the signs used.

Invoking with a maximum time is done using the optional parameter:

BC = GD_LINEAR SS 1 R_MOMENTUM1 0 VELOCITY1 0 {web_speed/time_max} 0.
BC = GD_TIME SS 1 R_MOMENTUM1 0 LINEAR 0 0 1. {time_max}
BC = GD_LINEAR SS 1 R_MOMENTUM1 0 VELOCITY1 0 0. -1.

Technical Discussion¶

This boundary condition building block is very useful for imposing time-dependent boundary conditions with some fairly standard functional forms without the inconvenience of writing a user-defined boundary condition. Boundary conditions for pulsating flow, piston motion, roll-eccentricity effects in coating, time-evolving temperature transients, etc. can all be constructed using this card. The examples at the end of this section on GD_* options will help the user construct such functions.

GD_CIRC¶

BC = GD_CIRC SS <bc_id> <equation_name> <integer1> <variable_name> <integer2> <float1> <float2> <float3>

Description / Usage¶

(PCC/VARIED)

This boundary condition of type Category 1 (see discussion) is used to impose a quadratic function for any nodal variable using the residual function form

\[-{C_1}^2 + C_3 \left( x - C_2\right)^2 = 0.\]

where \(C_1\), \(C_2\), and \(C_3\) are the constant values (<float>) and \(x\) represents any variable (<variable_name>). This boundary condition card can be used in combination with any of the other GD_* conditions as a building block to construct more complicated conditions. GD_CIRC happens to be a convenient building block for circles or elliptical functions (see examples below). Moreover, the resulting boundary condition can be applied as a strong residual replacement to any differential equation type. Please see the examples on all of these cards for details and instructive uses. Definitions of the input parameters are as follows: (convenient for circles):

GD_CIRC: Name of the boundary condition (<bc_name>).
SS: Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>: The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<equation_name>: A character string indicating the equation to which this boundary condition is applied. See the list of permissible values in the introduction to the Category 1 BCs following the Number of BC card.
<integer1>: Species number of the mass transport equation. The value should be 0 unless the <equation_name> is of type R_MASS.
<variable_name>: A character string indicating the variable that should be fixed. See the list of permissible values in the introduction to the Category 1 BCs following the Number of BC& card.
<integer2>: Species number of the concentration variable. The value should be 0 unless the <variable_name> is of type MASS_FRACTION.
<float1>: Radius \(C_1\). This should appear in only one GD_CIRC condition on each boundary.
<float2>: Origin \(C_2\).
<float3>: Ellipticity \(C_3\).

Examples¶

Following is a sample set of cards:

BC = GD_CIRC SS 1 R_MESH_NORMAL 0 MESH_POSITION1 0 1. 1. 1.
BC = GD_CIRC SS 1 R_MESH_NORMAL 0 MESH_POSITION2 0 0. 1. 1.

This set of cards can be used to prescribe a mesh distinguishing condition for a mesh surface with a quadratic dependence on x and y, a circle center at [1., 1.], and a radius of 1.0 (note the radius only appears on one card).

GD_TABLE¶

BC = GD_TABLE SS <bc_id> <equation_name> <integer1> <variable_name> <integer2> <scale> <interpolation> [FILE = <fname>]

Description / Usage¶

(PCC/VARIED)

This card is used to specify arbitrary, univariate (one abscissa and one ordinate: x1 - x2) data for boundary conditions on two-dimensional boundaries, e.g., the inlet velocity profile of a non-Newtonian fluid in a two-dimensional channel. The GD_TABLE specification differs slightly from the other cards in this category: the data are scalable and the data can be read from a file. Like the other GD_* cards, this card can be used as an additive building block for more complicated conditions. The examples below and at the end of the GD_* section will provide more detailed guidance.

Definitions of the input parameters are described next. Differences between this card and other GD_* cards are pointed out.

GD_TIME: Name of the boundary condition (<bc_name>).
SS: Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>: The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<equation_name>: A character string indicating the equation to which this boundary condition is applied. See the list of permissible values in the discussion above for Category 1. In contrast to other GD_* cards, this parameter also serves to identify the equation that is being supplanted.
<integer1>: Species number of the mass transport equation. The value should be 0 unless the <equation_name> is of type R_MASS.
<variable_name>: A character string indicating the variable that should be used in the function. See the list of permissible values in the discussion above for Category 1. For this card, in contrast to other GD_* cards, this parameter also identifies what value is to serve as abscissa when interpolating the table.
<integer2>: Species number of the concentration variable.The value should be 0 unless the <variable_name> is of type MASS_FRACTION.
<scale>: A floating point value by which to multiply the ordinate list after interpolation. It can be used to scale the table values or change their sign, e.g. C₀, scale factor in f(x₁) = C₀ * x₂
<interpolation>: Specifies the method to use in interpolating between supplied data points. Currently the only choice available is LINEAR, which invokes a simple linear interpolation method. Alternative methods will/can be added latter as required or requested.

The table data will be read from within the input deck itself (following the GD_TABLE BC card). The end of the table is signaled by the keywords “END TABLE.” (See the second example below.) An alternative to this method is to read a file with table data.

[FILE = <fname>]: The optional keyword ‘FILE =’ indicates that the table data is to be read from a separate file identified by <fname>.

Note that this boundary condition card functions as every other GD condition, be it LINEAR, QUADRATIC, POLYNOMIAL, or in this case TABULAR. It is used simple as a piece of a residual on the appropriate equation. Hence, it usually requires more than one GD card to completely specify the boundary condition.

Examples¶

Following is a sample card set in which the table data is to be read from an external file called upstream_land.dat:

BC = GD_LINEAR SS 1 R_MESH_NORMAL 0 MESH_POSITION2 0 0. -1.
BC = GD_TABLE SS 1 R_MESH_NORMAL 0 MESH_POSITION1 0 1.0 LINEAR
FILE=upstream_land.dat

This card set first creates a linear term in MESH_POSITION2, which is the y-coordinate of the mesh points along side set 1. The second, GD_TABLE card then creates a table of y-coordinate values based on x-mesh position. This boundary condition describes a land/filet composite geometry with x-y data points.

Following is a sample card, where the table data is to be read directly from the input deck:

BC = GD_TABLE SS 1 R_MOMENTUM1 0 MESH_POSITION2 0 1.0 LINEAR

$ r/R         Uz
0.000000      1.666667
0.050000      1.666458
0.100000      1.665000
0.150000      1.661042
0.200000      1.653333
0.250000      1.640625
0.300000      1.621667
.
.
0.900000      0.451667
0.950000      0.237708
1.000000      0.000000
END TABLE

This table is used to specify the radial dependence of an axial velocity profile along the specified side set.

Technical Discussion¶

This capability is widely used for geometry and velocity profile boundary conditions that do not have a convenient closed form. Note that for geometry specifications you cannot specify multi-valued functions, like for a cutback angle.

References¶

GTM-021.0: Multiparameter continuation and linear stability analysis on highly deformable meshes in Goma, M. M. Hopkins, June 22, 2000

Usage Notes on the GD Cards¶

Following are several examples of uses of the Generalized Dirichlet conditions:

For a circular boundary ( with radius 1, center at (0,0), \(x^2 + y^2 = 1\) ):

BC = GD_PARAB SS   1   R_MESH2 0 MESH_POSITION2     0   -1.   0.   1.
BC = GD_PARAB SS   1   R_MESH2 0 MESH_POSITION1     0   -0.   0.   1.

For a planar boundary ( \(2x + y = 1\) )

BC = GD_LINEAR SS   1   R_MESH1 0 MESH_POSITION1     0   -1.   2.
BC = GD_LINEAR SS   1   R_MESH1 0 MESH_POSITION2     0   0.   1.

For a parabolic inflow velocity profile ( \(u = 1 – 2y – 3y^2\) ):

BC = GD_LINEAR SS   4   R_MOMENTUM1 0 VELOCITY1     0   0.   -1.
BC = GD_PARAB SS   4   R_MOMENTUM1 0 MESH_POSITION2     0   1.   -2.   -3.

For a distinguishing condition where the mesh is an iso-concentration surface (\(C = 0.2\) with mesh equations rotated):

BC = GD_CONST SS   2   R_MESH_NORMAL 0 MASS_FRACTION     0   0.  2

For a temperature boundary condition with APREPRO constants \(C_i\) of the form

\[T = C_1 + C_2x + C_3x^2 + C_4x^3 + C_5x^4 + C_6x^5 + C_7x^6\]

BC = GD_LINEAR SS   2   R_ENERGY 0 TEMPERATURE     0   -1
BC = GD_POLYN SS   2   R_ENERGY 0 MESH_POSITION1     0   {c1 c2 c3 c4 c5 c6 c7}

Note, in the first three examples, two cards are combined to create a single boundary condition that is a function of two variables. Thus, with a little creativity, the Generalized Dirichlet conditions can replace many of the other boundary condition types.

To help generalize the Dirichlet conditions even more, GD_TIME can be used to modulate any combination of spatial GD conditions (the CONST, LINEAR, PARAB, POLYN, CIRC and TABLE options above) which appears prior to the set. Some examples here are warranted:

For a parabolic inflow velocity profile which is ramped from zero to a linearly growing multiplier times ( \(u = 1 – 2y – 3y^2\) ):

BC = GD_PARAB SS   4   R_MOMENTUM1 0 MESH_POSITION2     0   1.   -2.   -3.
BC = GD_TIME SS   4   R_MOMENTUM1   0   LINEAR     0   0.   1.
BC = GD_LINEAR SS   4   R_MOMENTUM1   0   VELOCITY1      0   0.   -1.

(This set of 3 conditions actually applies \(f(x, y, z, t, u) = 1t \left(1 – 2y – 3y^2 \right) – u = 0\) in place of the x-momentum equation. )

For a sinusoidally time-varying roller surface with equation \((x – x_0)^2 + (y – y_0)^2 = {R_0}^2\) with a frequency of 2. and a phase lag of 10:

BC = GD_PARAB SS   1   R_MESH_NORMAL   0   MESH_POSITION2 0 {x0*x0 + y0*y0 - R0*R0} {-2.*y0} 1
BC = GD_PARAB SS   1   R_MESH_NORMAL   0   MESH_POSITION1     0 {0.}   {-2.*x0} 1
BC = GD_TIME SS   1   R_MESH_NORMAL   0   SINUSOIDAL     0   10.   2.

This set of cards applies \(f(x, y, z, t) (x – x_0)^2 + (y – y_0)^2 - \sin(2t + 10) {R_0}^2 = 0\) to the normal component of the mesh equations along side set 1.

For a sinusoidally varying gap on a slot coater, the substrate has been made to oscillate according to \(f(x, y, t) = y – 3 \sin(t/4 + 5) = 0\) :

BC = GD_LINEAR SS   9   R_MESH2   0   MESH_POSITION1     0   -3.  0   0.
BC = GD_TIME SS   9   R_MESH2   0   SINUSOIDAL     0   5.   0.25
BC = GD_LINEAR SS   9   R_MESH2   0   MESH_POSITION2     0   0.   1.0

Setting the u-velocity on an inlet boundary for a power law fluid:

BC = GD_LINEAR SS   1   R_MOMENTUM1   0   VELOCITY1     0   0.   -1.
BC = GD_TABLE SS   1   R_MOMENTUM1   0   MESH_POSITION2 0 1.0 LINEAR

$ r/R         Uz
0.000000      1.666667
0.050000      1.666458
0.100000      1.665000
0.150000      1.661042
0.200000      1.653333
0.250000      1.640625
0.300000      1.621667
.             .
.             .
.             .
0.900000      0.451667
0.950000      0.237708
1.000000      0.000000
END TABLE

Setting the inlet concentration profile for species 0 from data in y0.table

BC = GD_LINEAR SS   1   R_MASS   0   MASS_FRACTION     0   0.0   -1.0
BC = GD_TABLE SS   1   R_MASS   0   MESH_POSITION2 0 1.0 LINEAR FILE = y0.table

Setting the inlet concentration profile for species 0 from an implicit relation.

Occasionally, we have analytic representations that are in the wrong form. For example, in particulate suspension modelling, a relation exists that gives the radial coordinate as a function of the concentration, i.e. \(r = F(C)\), where \(F\) is a non-linear relation. We would prefer it the other way around. We can use GD_TABLE to solve this dilemma. First, a file is prepared with the two columns, eqn.table for example:

C_0	F(C_0)
C_1	F(C_1)
.	.
.	.
C_N	F(C_N)

This just requires function evaluation. In the input deck, we then use the following cards

BC = GD_LINEAR SS   1   R_MASS   0   MESH_POSITION2     0   0.0   -1.0
BC = GD_TABLE SS   1   R_MASS   0   MASS_FRACTION 0 1.0 LINEAR FILE = eqn.table

and the right inlet concentration profile results.

TABLE_WICV¶

BC = TABLE_WICV SS <bc_id> {abscissa} {ordinate} {scale} {interpolation} [FILE = <fname>]

Description / Usage¶

(WIC/VECTOR VARIED)

This boundary allows the user to supply boundary data for vector weak integrated boundary conditions. See the TABLE_WICS card for scalar weak integrated boundary conditions. A prime example of the use of the TABLE_WICV card is application of a force for a solid deformation problem.

Definitions of the input parameters are as follows:

TABLE_WICV

Name of the boundary condition (<bc_name>).

SS

Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.

<bc_id>

The boundary flag identifier, an integer associated with TABLE_WICV that identifies the boundary location (side set in EXODUS II) in the problem domain.

{abscissa}

For one-dimensional tables (i.e. for use in 2D problems), the choices are restricted to one of the three coordinate directions. Use the strings X, Y or Z to identify the direction of choice. For two-dimensional tables (i.e. for use in 3D problems) use XY, XZ, YX, YZ, ZX, or ZY to denote the coordinate of the first and second columns in the table.

{ordinate}

This string identifies the equation of the weak integrated boundary term that the boundary data is added to. For example, use of the VELOCITY1 string will cause the table data to be used for all components of the liquid traction in the boundary integral for the liquid momentum equations. See the following table.

String	replaces	Equation
VELOCITY1 or U	liquid tractions	R_MOMENTUM[1-3]
MESH_DISPLACEMENT1 or DX or MESH_POSITION1	mesh tractions	R_MESH[1-3]
SOLID_DISPLACEMENT1	solid tractions	R_SOLID[1-3]

{scale}

A floating point scale multiplier which can be used to scale the tabular data. The boundary data used will be the product of {scale} and the tabular data.

{interpolation}

This is the method chosen to interpolate between supplied data points.

For one-dimensional tables, the choices are LINEAR, which denotes linear interpolation, QUADRATIC, which denotes quadratic Lagrangian interpolation and requires an odd number of data points, and QUAD_GP, which denotes quadratic interpolation where the data points represent Gauss point values. 3N data points (see Technical Discussion) are required for QUAD_GP interpolation.

For two-dimensional tables, BIQUADRATIC is currently the only choice. The first two columns of the table should define a rectangular, mapped grid where the second coordinate changes more quickly than the first. More complicated methods could be added latter.

[FILE = <fname>]

The keyword “FILE =” indicates that the table data be read from a separate file identified by <fname>. This parameter is optional and if it is left out the table data will be read from the input deck itself following the TABLE_WICV card. In this latter case, the end of the table is signaled by the keywords “END TABLE”. Note that the file specified by FILE = is fully apreproable, i.e., it will be preprocessed by APREPRO before reading if APREPRO is enabled.

Examples¶

Following is a sample card:

BC = TABLE_WICV SS 12 ZX MESH_DISPLACEMENT1 BIQUADRATIC FILE = load.table

load.table:

 0   0   6   0
 1   0   4   0
 0   0   3   0
 1   0   1   0

Technical Discussion¶

The table data itself appears as columns of numbers. One-dimensional TABLE_WICV tables have three columns (column1=abscissa, column2=ordinate component1, column3=ordinate component2), whereas two-dimensional TABLE_WICV tables have five columns (column1=abscissa1, column2=abscissa2, column3=ordinate component1, column4=ordinate component2, column5=ordinate component3). Goma will try to read float values from any line whose first parameter can be converted to a float.

The QUAD_GP interpolation option is meant for the case when the table data comes from another finite element model or another Goma run and the data is most readily available at the integration points of the finite element mesh. Hence, with quadratic Gaussian quadrature, there are three data points per element. N is the number of elements from the model that the data is coming from and therefore 3N data points are the total expected.

The user is also referred to the section on Boundary Condition Types at the beginning of the Boundary Condition Specifications. In particular, look at the discussion of Weakly Integrated Conditions (WIC).

TABLE_WICS¶

BC = TABLE_WICS SS <bc_id> {abscissa} {ordinate} {scale} {interpolation} [FILE = <fname>]

Description / Usage¶

(WIC/VARIED)

This boundary allows the user to supply boundary data for scalar weak integrated boundary conditions. See the TABLE_WICV card for vector weak integrated boundary conditions. A prime example of the use of the TABLE_WICS card is application of heat flux for a thermal problem.

Definitions of the input parameters are as follows:

TABLE_WICS: Name of the boundary condition (<bc_name>).
SS: Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>: The boundary flag identifier, an integer associated with TABLE_WICS that identifies the boundary location (side set in EXODUS II) in the problem domain.
{abscissa}: For one-dimensional tables (i.e. for use in 2D problems), the choices are restricted to one of the three coordinate directions. Use the strings X, Y or Z to identify the direction of choice. For two-dimensional tables (i.e. for use in 3D problems) use XY, XZ, YX, YZ, ZX, or ZY to denote the coordinate of the first and second columns in the table.
{ordinate}: This string identifies the equation of the weak integrated boundary term that the boundary data is added to. For example, use of the VELOCITY1 string will cause the table data to be used for the x-component of the liquid traction in the boundary integral for the x-momentum equation. See the following table.

String	replaces	Equation
VELOCITY1 or U	liquid x-traction	R_MOMENTUM1
VELOCITY2 or V	liquid y-traction	R_MOMENTUM2
VELOCITY3 or W	liquid z-traction	R_MOMENTUM3
TEMPERATURE	diffusive energy flux	R_ENERGY
MESH_DISPLACEMENT1 or DX or MESH_POSITION1	mesh x-traction	R_MESH1
MESH_DISPLACEMENT2 or DY or MESH_POSITION2	mesh y-traction	R_MESH2
MESH_DISPLACEMENT3 or DZ or MESH_POSITION3	mesh z-traction	R_MESH3
SOLID_DISPLACEMENT1	solid x-traction	R_SOLID1
SOLID_DISPLACEMENT2	solid y-traction	R_SOLID2
SOLID_DISPLACEMENT3	solid z-traction	R_SOLID3
S[1-3][1-3]_[1-7]	polymer mode traction	R_STRESS[1-3][1-3]_[1-7]

{scale}

A floating point scale multiplier which can be used to scale the tabular data. The boundary data used will be the product of {scale} and the tabular data.

{interpolation}

This is the method chosen to interpolate between supplied data points.

For one-dimensional tables, the choices are LINEAR, which denotes linear interpolation, QUADRATIC, which denotes quadratic Lagrangian interpolation and requires an odd number of data points, and QUAD_GP, which denotes quadratic interpolation where the data points represent Gauss point values. 3N data points (see Technical Discussion) are required for QUAD_GP interpolation.

For two-dimensional tables, BIQUADRATIC is currently the only choice. The first two columns of the table should define a rectangular, mapped grid where the second coordinate changes more quickly than the first. More complicated methods could be added latter.

[FILE = <fname>]

The keyword “FILE =” indicates that the table data be read from a separate file identified by <fname>. This parameter is optional and if it is left out the table data will be read from the input deck itself following the TABLE_WICS card. In this latter case, the end of the table is signaled by the keywords “END TABLE”. Note that the file specified by FILE = is fully apreproable, i.e., it will be preprocessed by APREPRO before reading if APREPRO is enabled.

Examples¶

Following is a sample card:

BC = TABLE_WICS SS 12 X TEMPERATURE QUADRATIC FILE =heatflux.table

heatflux.table:

0    1.0
5    1.5
0    1.75
5    2.0
0    2.0

Technical Discussion¶

The table data itself appears as columns of numbers. One-dimensional TABLE_WICS tables have two columns (column1=abscissa, column2=ordinate), whereas twodimensional TABLE_WICS tables have three columns (column1=abscissa1, column2=abscissa2, column3=ordinate). Goma will try to read float values from any line whose first parameter can be converted to a float.

The QUAD_GP interpolation option is meant for the case when the table data comes from another finite element model or another Goma run and the data is most readily available at the integration points of the finite element mesh. Hence, with quadratic Gaussian quadrature, there are three data points per element. N is the number of elements from the model that the data is coming from and therefore 3N data points are the total expected.

The user is also referred to the section on Boundary Condition Types at the beginning of the Boundary Condition Specifications. In particular, look at the discussion of Weakly Integrated Conditions (WIC).

TABLE¶

BC = TABLE SS <bc_id> {X|Y|Z|TIME} {ordinate} [species] {interpolation} [FILE = <fname>] [NAME = <identifier>]

Description / Usage¶

(PCC/VARIED))

This boundary condition is a stand-alone version of the more complicated GD_TABLE card. It allows the user to supply arbitrary univariate (one abscissa and one ordinate) data about the spatial variation of unknowns fields on a boundary. The abscissa will be one of the three spatial coordinates or time and the ordinate is one of a choice of unknown field variables. All TABLE_BC conditions must have attached tabular data as a list of paired float values either directly following the card or in a separate file (identified on the card). The list of data pairs is terminated by the string “END TABLE” on its own line.

Definitions of the input parameters are as follows:

TABLE: Name of the boundary condition.
SS: Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>: The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
{X|Y|Z|TIME}: A char_string that identifies the independent table variable (abscissa). The strings X,Y, and Z refer of course to the three spatial coordinates. Depending on the choice here, the x, y, or z coordinate value at a given point, respectively, is used to obtain an interpolated ordinate value using the attached table data. If the TIME string appears here, however, the current simulation time is used to interpolate an ordinate value. This single value is applied uniformly to the sideset.
{ordinate}: This string associates a variable type with the values of the ordinate in the attached table. It also identifies the equation that is supplanted by the boundary condition on the sideset. The following table lists the available string choices and the corresponding equation component clobbered by the boundary condition.

String	replaces	Equation*
VELOCITY1 or U		R_MOMENTUM1
VELOCITY2 or V		R_MOMENTUM2
VELOCITY3 or W		R_MOMENTUM3
MASS_FRACTION or Y or SPECIES		R_MASS
TEMPERATURE		R_ENERGY
MESH_DISPLACEMENT1 or DX		R_MESH1
MESH_DISPLACEMENT2 or DY		R_MESH2
MESH_DISPLACEMENT3 or DZ		R_MESH3
PRESSURE or P		R_PRESSURE
SOLID_DISPLACEMENT1 or DX_RS		R_SOLID1
SOLID_DISPLACEMENT2 or DY_RS		R_SOLID2
SOLID_DISPLACEMENT3 or DZ_RS		R_SOLID3
SHEAR_RATE or SH		R_SHEAR_RATE

String	replaces	Equation*
S11		R_STRESS11
S12		R_STRESS11
S22		R_STRESS11
S13		R_STRESS11
S23		R_STRESS11
S33		R_STRESS11

String	replaces	Equation*
S11_1		R_STRESS11_1
S12_1		R_STRESS12_1
S22_1		R_STRESS22_1
S13_1		R_STRESS13_1
S23_1		R_STRESS23_1
S33_1		R_STRESS33_1

String	replaces	Equation*
S11_2		R_STRESS11_2
S12_2		R_STRESS12_2
S22_2		R_STRESS22_2
S13_2		R_STRESS13_2
S23_2		R_STRESS23_2
S33_2		R_STRESS33_2

String	replaces	Equation*
S11_3		R_STRESS11_3
S12_3		R_STRESS12_3
S22_3		R_STRESS22_3
S13_3		R_STRESS13_3
S23_3		R_STRESS23_3
S33_3		R_STRESS33_3

String	replaces	Equation*
S11_4		R_STRESS11_4
S12_4		R_STRESS12_4
S22_4		R_STRESS22_4
S13_4		R_STRESS13_4
S23_4		R_STRESS23_4
S33_4		R_STRESS33_4

String	replaces	Equation*
S11_5		R_STRESS11_5
S12_5		R_STRESS12_5
S22_5		R_STRESS22_5
S13_5		R_STRESS13_5
S23_5		R_STRESS23_5
S33_5		R_STRESS33_5

String	replaces	Equation*
S11_6		R_STRESS11_6
S12_6		R_STRESS12_6
S22_6		R_STRESS22_6
S13_6		R_STRESS13_6
S23_6		R_STRESS23_6
S33_6		R_STRESS33_6

String	replaces	Equation*
S11_7		R_STRESS11_7
S12_7		R_STRESS12_7
S22_7		R_STRESS22_7
S13_7		R_STRESS13_7
S23_7		R_STRESS23_7
S33_7		R_STRESS33_7

[species]: An optional integer parameter that identifies the index of the appropriate species. Note, it should appear only when the <ordinate> string is MASS_FRACTION.
{interpolation}: A char_string parameter that identifies the method chosen to interpolate between the attached table data points. For one-dimensional tables, the choices are LINEAR, which denotes simple linear interpolation, and QUADRATIC, which denotes quadratic Lagrangian interpolation. Note that the latter requires an odd number of data points be supplied in the table.
[FILE = <fname>]: The optional char_string keyword “FILE =” indicates that the table data be read from a separate file identified by <fname>. This parameter is optional and if it is left out the table data will be read from the input deck itself following the TABLE BC card. Note that the file specified by <fname> will be first preprocessed by APREPRO if that option was enabled on the command line. This is a useful feature that allows for a quick way to introduce analytic expressions onto boundaries.
[NAME = <identifier>]: The optional char_string keyword NAME = allows for a set of table data to be attached to the char_string parameter <identifier>. This option can only be used if the table data is read from a separate file identified by FILE = <fname>. In this case, the file <fname> is scanned for the char_string “identifier:” (note the colon). Once found the table data is read until encountering END TABLE. This option permits multiple sets of data in the same file.

The second half of the TABLE_BC implementation is the tabular data itself. In the TABLE boundary condition, it consists of a set of paired float values, each pair on its own line. This data should follow directly after the TABLE boundary condition card if the FILE = option is not used. If a value for <fname> is supplied, the table data should be written in the file so indicated. Note that in most implementations of UNIX, <fname> can include a complete path specification in case the datafile is in a different directory than the run directory. In either case, input deck or separate file, the set of data table pairs should always be terminated by the string END TABLE to terminate reading of the data. When reading the table data, Goma attempts to read a float value on each line. If it is unsuccessful, e.g., a string might start the line, it will proceed to the next line. If it is successful, it will attempt to read a second float value to complete the data pair. An unsuccessful read here is an error. Once the second value is read, however, the remainder of the line is discarded and the next line is read. This procedure permits inclusion of comments within. See the next section for some examples.

Thus,

3. 1.e-4
1. 3. % this is a good example
$ 1. 40.0
$ I have no idea where the following data came from
    3.4   2.1
    1.e-2   6000.0

will result in four data points being read, whereas, both of the following

6.443   3.43c
5.4099   % 099.0

will result in an error.

Examples¶

The following is an example of a tabular data set that will be read correctly

$ This data came from M. Hobbs. God only knows where he got it.
T   k
0.5 1.e-4
1. 15.   % I’m not particularly sure about this one.
3.4   8.1
5.6   23.0
$ 1.0 40.0

In this case, four data pairs will be read to form the table.

Example usage of the TABLE card follows:

Setting the u-velocity on an inlet boundary for a power law fluid:

BC = TABLE SS 1 Y U LINEAR
$ r/R Ux
0.000000 1.666667
0.050000 1.666458
0.100000 1.665000
0.150000 1.661042
0.200000 1.653333
0.250000 1.640625
0.300000 1.621667
..
..
0.900000 0.451667
0.950000 0.237708
1.000000 0.000000
END TABLE

Setting the inlet concentration profiles for species 0 and species 1 from data in y.table:

BC = TABLE SS 1 Y SPECIES 0 QUADRATIC FILE = y.table NAME = y0
BC = TABLE SS 1 Y SPECIES 1 QUADRATIC FILE = y.table NAME = y1

The file y.table contains:

y0:
        0.   1.0
        0.25 0.75
        0.5 0.60
        0.75 0.30
        1.0 0.20
END TABLE
y1:
        0. 0.0
        0.25 0.2
        0.5 0.3
        0.75 0.5
        1.0 0.8
END TABLE

Setting a temperature history on a sideset

BC = TABLE SS 1 TIME TEMPERATURE LINEAR
0.0   0.0
10.0   373.0
40.0   373.0
50.0   500.0
100.0   500.0
150    0.0
100000.0   0.0
END TABLE

Technical Discussion¶

The TABLE boundary condition provides similar functionality to the GD_TABLE boundary condition but with a simplified interface the notion behind both cards is that often information on boundaries is known only as a set of data points at specific positions on the boundary. The TABLE boundary condition can use that boundary information to provide interpolated values at nodal locations and then impose them as a strong point collocated condition.

Interpolation orders for this method are limited to LINEAR and QUADRATIC with the latter requiring an odd number of data points be supplied in the table.

Category 2: Mesh Equations¶

The boundary conditions in this section involve the mesh motion equations in LAGRANGIAN or ARBITRARY form (cf. Mesh Motion card). These conditions can be used to pin the mesh, specify its slope at some boundary intersection, apply a traction to a surface, etc. Several more boundary conditions that are applied to the mesh motion equations but include other problem physics are also available.

DISTNG¶

BC = DISTNG SS <bc_id> <float>

Description / Usage¶

(PCC/ROTATED MESH)

This boundary condition card is used to specify a distinguishing condition for mesh motion based on an isotherm, viz. the distinguishing condition forces the mesh boundary to which it is applied to take on a position such that the temperature is constant and at the specified value, all along the boundary. This condition causes the vector mesh motion equations (viz. mesh1, mesh2, and mesh3 on EQ cards) to be rotated into normal-tangential form. In two dimensions, this condition is applied to the normal component automatically; in three dimensions it is suggested to put it on the normal component, as specified by the ROT conditions. Definitions of the input parameters are as follows:

DISTNG	Name of the boundary condition (<bcname>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float>	Value of temperature/isotherm. To apply a variable temperature, e.g., as a function of the concentration, it is suggested that the user-defined boundary conditions be used, like SPLINE or GEOM.

Examples¶

The following is a sample input card:

BC = DISTNG SS 123 273.0

This card forces the boundary defined by EXODUS II side set number 123 to conform to the isotherm temperature of 273.0.

Technical Discussion¶

The mathematical form of this distinguishing condition is as follows:

\[T - T_{\mathrm{mp}} = 0\]

where \(T_{\mathrm{mp}}\) is the specified temperature parameter. This condition has been used extensively for macroscale and microscale melting problems, whereby one needs to distinguish a molten region from a solidified or mushy region with liquidus and solidus temperatures. In three dimensions, usage needs to be completed with a companion ROT input card which directs the equation application of the condition.

FAQs¶

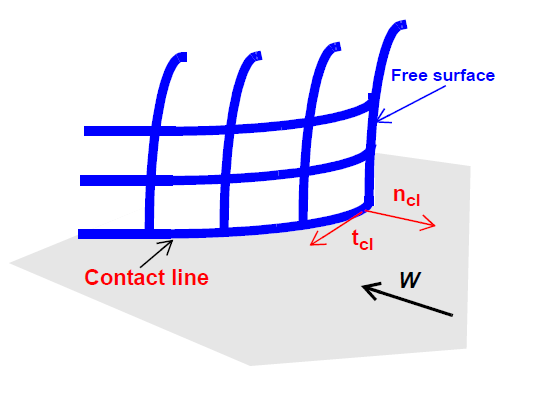
Continuation Strategies for Free Surface Flows In free surface problems, there exists one or more boundaries or internal surfaces whose position(s) are unknown a priori. As such, the geometry of the problem becomes part of the problem and must be determined together with the internal physics. Most problems of this sort cannot be solved with a trivial initial guess to the solution vector, mainly because the conditions which determine the surface position are closely coupled to the active physics in the bulk. Thus, these problems require continuation (zero or higher order) to achieve a converged solution to a desired state. The continuation strategy typically involves turning on and off the conditions which distinguish the position of the free surface(s); one such strategy is described in this FAQ.

Distinguishing conditions in Goma serve two purposes: (1) they can be used to locate a surface whose position depends on internal and interfacial transport phenomena, and (2) they can be used to prescribe solid boundary position or motion. The first type of condition contains field variables needed to locate the interface or free surface position, and hence ties the mesh motion to the problem physics, i.e., mass, momentum, and energy transport phenomena. Currently, the side-set boundary conditions of type DISTNG, KINEMATIC, and KIN_LEAK fall into this class. The second type of condition requires only geometrical information from the mesh, and, although geometrically couples the mesh motion to the problem physics, it tends not to be so tightly coupled. Currently, boundary conditions PLANE, PLANEX, PLANEY, PLANEZ, SPLINE, SPLINEX, SPLINEY, and SPLINEZ fall into this class.

In two dimensions, there is no need to use PLANEX, PLANEY, PLANEZ, SPLINEX, SPLINEY, and SPLINEZ. Because the code automatically rotates the mesh residual equations and the corresponding Jacobian entries into normal-tangential form on the boundary, SPLINE, PLANE, and DISTNG are the only cards required to specify the position of the boundary. Currently, in three dimensions, the logic for the same rotation concept is not totally functional, and one must use the PLANEX, etc. cards to designate which component of the mesh stress residual equation receives the distinguishing conditions.

If cards DISTNG, KINEMATIC, and KIN_LEAK, i.e., distinguishing conditions of type 1, are absent in any simulation, then any initial guess for the transport field equations, i.e., energy and momentum, has a chance of converging, as long as the initial mesh displacement guess is within the radius of convergence of the mesh equations and associated boundary conditions. For example, if the side sets of the EXODUS II database mesh correspond somewhat closely to what is prescribed with PLANE and SPLINE-type conditions, then an initial guess of the NULL vector has a good chance of converging, so long as the velocities and temperatures are within “converging distance.”

When conditions from the first class are present, i.e., either DISTNG, KIN_LEAK or KINEMATIC, then the following procedure should be followed:

Set the keyword for the Initial Guess character_string to zero, one, or random.
Obtain a solution (run Goma) with the initial guess for the free surfaces distinguished as KINEMATIC (or other) coming from the EXODUS II database, but without the KINEMATIC (or other) card(s). That is, “fix” those surfaces with either a PLANE or SPLINE command, or simply place no distinguishing condition on them (this works only if the grid has not been previously “stressed”, i.e., all the displacements are zero). The rest of the “desired” physics should be maintained. If any surface is distinguished as KINEMATIC, then it is highly advantageous to place a VELO_NORMAL condition on that surface for startup, and set the corresponding floating point datum to zero. This effectively allows the fluid to “slip” along that boundary as if it were a shear free condition.
Set the keyword in the Initial Guess character_string to read.
Copy the file named in SOLN file into the file named in GUESS file.
Release the free boundaries by taking off any current distinguishing condition cards and adding the appropriate KINEMATIC (or other) card. Adjust all other boundary conditions appropriately.
Run Goma, using a relaxed Newton approach (factor less than unity but greater than zero - e.g., 0.1) for complex flows.

When dealing with material surface boundaries distinguished by the kinematic boundary condition, the nature of that condition requires a non-zero and substantial component of velocity tangent to the surface upon start-up. In this case, it can be advantageous to use the VELO_TANGENT card to set the velocity along the free surface to some appropriate value prior to releasing the free surface (in the third step above). Of course this card will be removed in subsequent steps. Also, although not necessary, a smooth, “kinkless”, initial guess to the free surface shape is helpful because it reduces the amount of relaxation required on the Newton iteration.

Obtaining start-up solutions of most coating flow configurations is still an art. The best way to start up a coating flow analysis may be to acquire a “template” developed from a previous analysis of some closely related flows.

References¶

Allen Roach’s or Randy’s ESR tutorials. Perhaps these need to be put into the repository.

DXDYDZ¶

BC = {DX | DY | DZ} NS <bc_id> <float1> [float2]

Description / Usage¶

(DC/MESH)

This boundary condition format is used to set a constant X, Y, or Z displacement. Each such specification is made on a separate input card. These boundary conditions must be applied to node sets. Definitions of the input parameters are as follows:

{DX \| DY \| DZ}	Two-character boundary condition name (<bc_name>) that defines the displacement, where: DX - X displacement DY - Y displacement DZ - Z displacement
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	Value of the displacement (X, Y, or Z) defined above.
[float2]	An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

Following is a sample card which applies an X-displacement boundary condition to the nodes in node set 100, specifically an X-Displacement of 1.0. These displacements are applied immediately to the unknowns and hence result in immediate mesh displacements from the initial state.

BC = DX NS 100   1.0

This sample card applies the same condition as above, except as a residual equation that is iterated upon with Newton’s method.

BC = DX NS 100 1.0   1.0

The second float 1.0 forces this application. This approach is advisable in most situations, as the nodes are gradually moved as a part of the mesh deformation process; sudden movements, as in the first example, can lead to folds in the mesh.

Technical Discussion¶

Application of boundary conditions of the Dirichlet type on mesh motion requires different considerations than those on non-mesh degrees of freedom. Sudden displacements at a point, without any motion in the mesh surrounding that point, can lead to poorly shaped elements. It is advisable to apply these sorts of boundary conditions as residual equations, as discussed above. Examples of how these conditions are used to move solid structures relative to a fluid, as in a roll-coating flow, are contained in the references below.

References¶

GT-003.1: Roll coating templates and tutorial for GOMA and SEAMS, February 29, 2000, P. R. Schunk and M. S. Stay

GT-005.3: THE NEW TOTAL-ARBITRARY-LAGRANGIAN-EULERIAN (TALE) CAPABILITY and its applicability to coating with/on deformable media, August 6, 1999, P. R. Schunk.

DXUSER DYUSER DZUSER¶

BC = {DXUSER | DYUSER | DZUSER} SS <bc_id> <float_list>

Description / Usage¶

(PCC/MESH)

This boundary condition format is used to set a constant X, Y, or Z displacement as a function of any independent variable available in Goma. These boundary conditions require the user to edit the routines dx_user_surf, dy_user_surf, and/or dz_user_surf to add the desired models. These routines are located in the file user_bc.c. In the input deck each such specification is made on a separate input card. These boundary conditions must be applied to side sets. Definitions of the input parameters are as follows:

{DX_USER \| DY_USER \| DZ_USER}	Seven-character boundary condition name (<bc_name>) that defines the displacement, where: DX_USER - X displacement, user-defined DY_USER - Y displacement, user-defined DZ_USER - Z displacement, user-defined
SS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float_list>	A list of float values separated by spaces which will be passed to the user-defined subroutine so the user can vary the parameters of the boundary condition. This list of float values is passed as a one-dimensional double array to the appropriate C function.

Examples¶

Following is a sample card which applies an X-displacement boundary condition to the nodes in node set 100, with a functional form set by the user and parameterized by the single floating point number . These displacements are applied immediately to the unknowns and hence result in immediate mesh displacement from the initial state.

BC = DX_USER SS 100 1.0

Please consult the user-definition subroutines for examples.

References¶

No References.

DXYZDISTNG¶

BC = {DXDISTNG | DYDISTNG | DZDISTNG} SS <bc_id> <float>

Description / Usage¶

(PCC/MESH)

This boundary condition card is used to specify a distinguishing condition for mesh motion based on an isotherm, viz. the distinguishing condition forces the mesh boundary to which it is applied to take on a position such that the temperature is constant and at the specified value, all along the boundary. Although of the same mathematical form as the DISTNG boundary condition, this condition does not force a boundary rotation of the vector mesh residuals. Instead, it is recommended that the condition be chosen such that the predominant direction of the normal vector is close to one of the three Cartesian coordinates, X, Y, or Z. For example, if the boundary in question is basically oriented so that the normal vector is mostly in the positive or negative Y-direction, then DYDISTNG should be chosen. Definitions of the input parameters are as follows:

{DXDISTNG \| DYDISTNG \| DZDISTNG}	Eight-character boundary condition name (<bc_name>) that defines the distinguishing condition, where: DXDISTNG - X condition DYDISTNG - Y condition DZDISTNG - Z condition
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float>	Value of temperature isotherm. If one wanted to apply a variable temperature, e.g. as a function of the concentration, it is suggested that the user-defined boundary conditions be used.

Examples¶

The following is a sample input card:

BC = DYDISTNG SS 123 273.0

This card forces the boundary defined by EXODUS II side set number 123 to conform to the isotherm temperature of 273.0. Most importantly, the y-component of the mesh equation residuals is replaced by this condition.

Technical Discussion¶

The mathematical form of this distinguishing condition is as follows:

\[T - T_{\mathrm{mp}} = 0\]

where \(T_{\mathrm{mp}}\) is the specified temperature parameter. This condition has been used extensively for macroscale and microscale melting problems, whereby one needs to distinguish a molten region from a solidified or mushy region with liquidus and solidus temperatures. In three dimensions usage needs to be completed with a companion ROT input card which directs the equation application of the condition, even though rotations are not actually performed.

As a bit of software trivia, this is the first distinguishing condition ever written in Goma, and one of the first boundary conditions, period.

SPLINEXYZ/GEOMXYZ¶

BC = {bc_name} SS <bc_id> [floatlist]

Description / Usage¶

(PCC/MESH)

This card is used to specify a general surface (solid) boundary description for ALE (or in special cases LAGRANGIAN) type mesh motion (see Mesh Motion card). These boundary conditions are tantamount to SPLINE or GEOM, except that they do not invoke a mesh-equation vector residual rotation into normal-tangential form. Instead, SPLINEX or, equivalently, GEOMX invokes the geometric boundary condition on the x-component of the mesh equation residual, and so on. The card requires user-defined subroutines. Templates for these routines are currently located in the routine “user_bc.c”. Both a function routine, fnc, for function evaluation and corresponding routines dfncd1, dfncd2, and dfncd3 for the derivative of the function with respect to global coordinates are required. GEOMX and SPLINEX are exactly the same condition. SPLINE* usage is being deprecated. Note that it takes an arbitrary number of floating-point parameters, depending on the user’s needs.

Definitions of the input parameters are as follows:

{bc_name}	Boundary condition name that defines the general surface; the options are: SPLINEX/GEOMX - X general surface SPLINEY/GEOMY - Y general surface SPLINEZ/GEOMZ - Z general surface
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
[floatlist]	Constants to parameterize any f(x,y,z) = 0 function input in user-defined routine fnc.

Examples¶

The following is a sample input card:

BC = GEOMZ SS 10 1.0 100. 20.0 1001.0 32.0

applies a user-defined distinguishing condition parameterized by the list of floating points to the boundary defined by side set 10. Most importantly, the condition replaces the Z-component of the momentum equation.

Technical Discussion¶

The mathematical form of this distinguishing condition is arbitrary and is specified by the user in the fnc routine in user_bc.c. Derivatives of the user-specified function must also be provided so as to maintain strong convergence in the Newton iteration process. These functions are located next to fnc and are named dfncd1, dfncd2, and dfncd3.Several examples for simple surfaces exist in the template routine. In three dimensions, usage needs to be completed with a companion ROT input card which directs the equation application of the condition, even though rotations are not actually performed.

SPLINE/GEOM¶

BC = {SPLINE|GEOM} SS <bc_id> [floatlist]

Description / Usage¶

(PCC/ROTATED MESH)

This card is used to specify a general surface (solid) boundary description for ALE (or in special cases LAGRANGIAN) type mesh motion (see Mesh Motion card). Like most other distinguishing conditions, this condition causes the mesh-motion equations, viz. mesh1, mesh2, and mesh3, to be rotated into boundary normal-tangential form. The card requires user-defined subroutines. Templates for these routines are currently located in the routine “user_bc.c”. Both a function routine, fnc, for function evaluation and corresponding routines dfncd1, dfncd2, and dfncd3 for the derivative of the function with respect to global coordinates are required. The SPLINE condition is exactly the same and uses the same routine as the GEOM card option, and hence as of the time of this writing we are deprecating the use of SPLINE. Note that it takes an arbitrary number of floating-point parameters, depending on the user’s needs.

Definitions of the input parameters are as follows:

SPLINE/GEOM	Name of the boundary condition <bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
[floatlist]	Constants to parameterize any f(x,y,z) = 0 function input in user-defined routine fnc.

Examples¶

The following sample input card:

BC = SPLINE SS 10 1.0 100. 20.0 1001.0 32.0

applies a user-defined distinguishing condition, parameterized by the list of five floating point values, to the boundary defined by side set 10.

Technical Discussion¶

This condition, like DISTNG, PLANE, and others that can be applied to geometry, is applied to the normal component of the mesh motion equations along a boundary in two dimensions; in three dimensions application needs to be further directed with the ROT conditions. Examples of typical distinguishing conditions can be found in user_bc.c in the fnc routine and companion derivative routines.

PLANEXYZ¶

BC = {PLANEX | PLANEY | PLANEZ} SS <bc_id> <floatlist>

Description / Usage¶

(PCC/ MESH)

This boundary condition card is used to specify a planar surface (solid) boundary description as a replacement on the X, Y, or Z-component (PLANEX, PLANEY, PLANEZ, respectively) of the mesh equations (see EQ cards mesh1, mesh2, or mesh3). The form of this equation is given by

\[f(x, y, z) = ax + by + cz + d = 0\]

This mathematical form and its usage is exactly like the BC = PLANE boundary condition card (see PLANE for description), but is applied to the mesh motion equations without rotation. Definitions of the input parameters are given below; note that <floatlist> has four parameters corresponding to the four constants in the equation:

{PLANEX \| PLANEY \| PLANEZ}	Boundary condition name (<bc_name>) where: PLANEX - normal predominantly in X direction PLANEY - normal predominantly in Y direction PLANEZ - normal predominantly in Z direction
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	\(a\) in function \(f(x, y, z)\)
<float2>	\(b\) in function \(f(x, y, z)\)
<float3>	\(c\) in function \(f(x, y, z)\)
<float4>	\(d\) in function \(f(x, y, z)\)

Examples¶

Following is a sample input card for a predominantly X-directed surface (viz, as planar surface whose normal has a dominant component in the positive or negative X direction):

BC = PLANEX SS 101 1.0 1.0 -2.0   100.0

This boundary condition leads to the application of the equation \(1.0x + 1.0y – 2.0z = –100.0\) to the mesh1 equation on EXODUS II side set number 101.

Technical Discussion¶

These conditions are sometimes used instead of the more general PLANE boundary condition in situations where ROTATION (see ROT command section) leads to poor convergence of the matrix solvers or is not desirable for some other reason. In general, the PLANE condition should be used instead of these, but in special cases these can be used to force the application of the planar geometry to a specific component of the mesh stress equation residuals. Full understanding of the boundary rotation concept is necessary to understand these reasons (see Rotation Specifications).

References¶

GT-001.4: GOMA and SEAMS tutorial for new users, February 18, 2002, P. R. Schunk and D. A. Labreche

GT-007.2: Tutorial on droplet on incline problem, July 30, 1999, T. A. Baer

GT-013.2: Computations for slot coater edge section, October 10, 2002, T.A. Baer

GT-018.1: ROT card tutorial, January 22, 2001, T. A. Baer

PLANE¶

BC = PLANE SS <bc_id> <floatlist>

Description / Usage¶

(PCC/ROTATED MESH)

This card is used to specify a surface (solid) boundary position of a planar surface. It is applied as a rotated condition on the mesh equations (see EQ cards mesh1, mesh2 mesh3). The form of this equation is given by

\[f(x, y, z) = ax + by + cz + d = 0\]

Definitions of the input parameters are given below; note that <floatlist> has four parameters corresponding to the four constants in the equation:

PLANE	Name of the boundary condition name (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	\(a\) in function \(f(x, y, z)\)
<float2>	\(b\) in function \(f(x, y, z)\)
<float3>	\(c\) in function \(f(x, y, z)\)
<float4>	\(d\) in function \(f(x, y, z)\)

Examples¶

Following is a sample input card:

BC = PLANE SS 3 0.0 1.0 0.0 -0.3

results in setting the side set elements along the side set 3 to a plane described by the equation \(f(x, y, z, t) = y – 0.3 = 0\) .

Technical Discussion¶

This, like most boundary conditions on geometry with arbitrary grid motion, is applied to the weighted residuals of the mesh equation rotated into the normal-tangential basis on the boundary. Specifically, this boundary condition displaces the normal component after rotation of the vector residual equation, leaving the tangential component to satisfy the natural mesh-stress free state. That is to say, this boundary condition allows for mesh to slide freely in the tangential direction of the plane surface.

This boundary condition can be applied regardless of the Mesh Motion type, and is convenient to use when one desires to move the plane with time normal to itself.

References¶

GT-001.4: GOMA and SEAMS tutorial for new users, February 18, 2002, P. R. Schunk and D. A. Labreche

GT-013.2: Computations for slot coater edge section, October 10, 2002, T.A. Baer

MOVING_PLANE¶

BC = MOVING_PLANE <bc_id> <floatlist>

Description / Usage¶

(PCC/ROTATED MESH)

The MOVING_PLANE card is used to specify a surface (solid) boundary position versus time for a planar surface (cf. PLANE boundary condition card). It is applied as a rotated condition on the mesh equations (see EQ cards mesh1, mesh2, mesh3). The form of the equation is given by

\[f(x, y, z, t) = ax + by + cz + d + g(t) = 0\]

and the function \(g(t)\) is defined as

\[g(t) = \lambda_1t + \lambda_2t^2 + \lambda_3t^3\]

Definitions of the input parameters are given below; note that <floatlist> has seven parameters corresponding to the seven constants in the above equations:

MOVING_ PLANE	Name of the boundary condition name (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	\(a\) in function \(f(x, y, z, t)\)
<float2>	\(b\) in function \(f(x, y, z, t)\)
<float3>	\(c\) in function \(f(x, y, z, t)\)
<float4>	\(d\) in function \(f(x, y, z, t)\)
<float5>	\(\lambda_1\) coefficient in \(g(t)\)
<float6>	\(\lambda_2\) coefficient in \(g(t)\)
<float7>	\(\lambda_3\) coefficient in \(g(t)\)

Examples¶

The boundary condition card

BC = MOVING_PLANE SS 3 0. 1. 0. -0.3 0.1 0.0 0.0

results in a plane originally positioned at y = 0.3 to move at a velocity of -0.1, viz. the position of all nodes on the plane will follow:

\[f(x, y, z, t) = y - 0.3 + 0.1t = 0\]

Technical Discussion¶

This, like most boundary conditions on geometry with arbitrary grid motion, is applied to the weighted residuals of the mesh equation rotated into the normal-tangential basis on the boundary. Specifically, this boundary condition displaces the normal component after rotation of the vector residual equation, leaving the tangential component to satisfy the natural mesh-stress free state. That is to say, this boundary condition allows for mesh to slide freely in the tangential direction of the plane surface.

This boundary condition can be applied regardless of the Mesh Motion type, and is convenient to use in place of PLANE when one desires to move the plane with time normal to itself.

SLOPEXYZ¶

BC = {SLOPEX | SLOPEY | SLOPEZ} SS <bc_id> <floatlist>

Description / Usage¶

(SIC/MESH)

This boundary condition card applies a slope at the boundary of a LAGRANGIAN, TALE, or ARBITRARY solid (see Mesh Motion card) such that the normal vector to the surface is colinear with the vector specified as input, viz \(\underline{n} \cdot \underline{n}_{\mathrm{spec}} = 0\). Here \(\underline{n}_{\mathrm{spec}}\) is the vector specified component-wise via the three <floatlist> parameters on the input card. Definitions of the input parameters are as follows:

{SLOPEX \| SLOPEY \| SLOPEZ}	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	X-component of the slope vector \(\underline{n}_{\mathrm{spec}}\)
<float2>	Y-component of the slope vector \(\underline{n}_{\mathrm{spec}}\)
<float3>	Z-component of the slope vector \(\underline{n}_{\mathrm{spec}}\)

Examples¶

The following is a sample input card:

BC = SLOPEX SS 10 1.0 1.0 0.0

This card invokes a boundary condition on the normal component of the mesh residual momentum equations such that the outward facing surface normal vector along side set 10 is colinear with the vector [1.0, 1.0, 0.0]. This condition is applied to the x-component of the mesh residual equations.

Technical Discussion¶

See discussion for BC card SLOPE. The only difference in these conditions and the SLOPE conditions, is that the latter invokes rotation of the vector mesh residual equations on the boundary.

SLOPE¶

BC = SLOPE SS <bc_id> <float1> <float2> <float3>

Description / Usage¶

(SIC/ROTATED MESH)

This boundary condition card applies a slope at the boundary of a LAGRANGIAN, TALE, or ARBITRARY solid (see Mesh Motion card) such that the normal vector to the surface is colinear with the vector specified as input, viz \(\underline{n} \cdot \underline{n}_{\mathrm{spec}} = 0\) . Here \(\underline{n}_{\mathrm{spec}}\) the vector specified component-wise via the three <float> parameters on the input card. Definitions of the input parameters are as follows:

SLOPE	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	X-component of the slope vector \(\underline{n}_{\mathrm{spec}}\)
<float2>	Y-component of the slope vector \(\underline{n}_{\mathrm{spec}}\)
<float3>	Z-component of the slope vector \(\underline{n}_{\mathrm{spec}}\)

Examples¶

The following is a sample input card:

BC = SLOPE SS 10 1.0 1.0 0.0

This card invokes a boundary condition on the normal component of the mesh residual momentum equations such that the outward facing surface normal vector along side set 10 is colinear with the vector [1.0, 1.0, 0.0].

Technical Discussion¶

This condition, although not often used, allows for a planar boundary condition (cf. PLANE, PLANEX, etc.) to be specified in terms of a slope, rather than a specific equation. Clearly, at some point along the surface (most likely at the ends), the geometry has to be pinned with some other boundary condition (cf. DX, DY, DZ) so as to make the equation unique. This condition has the following mathematical form:

\[\underline{n} \cdot \underline{n}_{\mathrm{spec}} = 0\]

and is applied in place of the normal component of the mesh motion equations, i.e., it is a rotated type boundary condition. If used in three dimensions, it will require a rotation description with the ROT cards.

KINEMATIC¶

BC = KINEMATIC SS <bc_id> <float1> [integer]

Description / Usage¶

(SIC/ROTATED MESH)

This boundary condition card is used as a distinguishing condition on the mesh motion equations (viz. mesh1, mesh2, and mesh3 under the EQ card). It enforces the boundary of the mesh defined by the side set to conform to a transient or steady material surface, with an optional, pre-specified mass loss/gain rate. In two dimensions, this condition is automatically applied to the normal component of the vector mesh equations, which is rotated into normal-tangential form. In three dimensions, the application of this boundary condition needs to be further directed with the ROT cards (see Rotation Specifications). The application of this condition should be compared with KINEMATIC_PETROV and KINEMATIC_COLLOC.

Definitions of the input parameters are as follows:

KINEMATIC	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	Mass-loss (positive) or mass-gain (negative) velocity at the free boundary.
[integer]	Optional integer value indicating the element block id from which to apply the boundary condition.

Examples¶

The following sample card

BC = KINEMATIC SS 7 0.0

leads to the application of the kinematic boundary condition to the boundary-normal component of the mesh-stress equation on the boundary defined by side set 7.

Technical Discussion¶

The functional form of the kinematic boundary condition is:

\[\underline{n} \cdot \left( \underline{v} - \underline{v}_s \right) = \dot{m}\]

Here \(\underline{n}\) is the unit normal vector to the free surface, \(\underline{v}\) is the velocity of the fluid, \(\underline{v}_s\) is the velocity of the surface (or mesh), and \(\dot{m}\) is the mass loss/gain rate. In two dimensions this equation is applied to the normal component of the vector mesh position equation, and hence is considered as a distinguishing condition on the location of the mesh relative to the fluid domain.

FAQs¶

See the FAQ pertaining to “Continuation Strategies for Free Surface Flows” on the DISTNG boundary condition card.

References¶

GT-001.4: GOMA and SEAMS tutorial for new users, February 18, 2002, P. R. Schunk and D. A. Labreche

KINEMATIC_PETROV¶

BC = KINEMATIC_PETROV SS <bc_id> <float1> [integer]

Description / Usage¶

(SIC/ROTATED MESH)

This boundary condition card is used as a distinguishing condition on the mesh motion equations (viz. mesh1, mesh2, and mesh3 under the EQ card). It enforces the boundary of the mesh defined by the side set to conform to a transient or steady material surface, with an optional, pre-specified mass loss/gain rate. In two dimensions, this condition is automatically applied to the normal component of the vector mesh equations, which is rotated into normal-tangential form. In three dimensions, the application of this boundary condition needs to be further directed with the ROT cards (see ROTATION Specifications). Please consult the Technical Discussion for important inofrmation.

Definitions of the input parameters are as follows:

KINEMATIC_PETROV	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	Mass-loss (positive) or mass-gain (negative) velocity at the free boundary.
[integer]	Optional integer value indicating the element block id from which to apply the boundary condition.

Examples¶

The following sample card

BC = KINEMATIC_PETROV SS 7 0.0

leads to the application of the kinematic boundary condition to the boundary-normal component of the mesh-stress equation to the boundary defined by side set 7.

Technical Discussion¶

Important note: This condition is actually the same as the KINEMATIC condition but is applied with different numerics for special cases. Specifically, rather than treated in a Galerkin fashion with a weighting function equal to the interpolation function for velocity, the residual of the equation is formed as weighted by the directional derivative of the basis functions along the free surface. Specifically,

\[\int \left\{ \underline{n} \cdot \left( \underline{v} - \underline{v}_s \right) - \dot{m} \right\} \phi^i \, \mathrm{d}A = R^i = 0\]

where the nodal basis function \(\phi^i\) is replaced by \(\frac{\partial}{\partial s} \phi^i\) in the residual equation. Compare this to the KINEMATIC boundary condition description.

KINEMATIC_COLLOC¶

BC = KINEMATIC_COLLOC SS <bc_id> <float1>

Description / Usage¶

(PCC/ROTATED MESH)

This boundary condition card is used as a distinguishing condition on the mesh motion equations (viz. mesh1, mesh2, and mesh3 under the EQ card). It enforces the boundary of the mesh defined by the side set to conform to a transient or steady material surface, with an optional, pre-specified mass loss/gain rate. In two dimensions this condition is automatically applied to the normal component of the vector mesh equations, which is rotated into normal-tangential form. In three dimensions the application of this boundary condition needs to be further directed with the ROT cards (see Rotation Specifications). Definitions of the input parameters are as follows:

KINEMATIC_COLLOC	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	Mass-loss (positive) or mass-gain (negative) velocity at the free boundary.

Examples¶

The following sample card

BC = KINEMATIC_COLLOC SS 7 0.0

leads to the application of the kinematic boundary condition to the boundary-normal component of the mesh-stress equation to the boundary defined by side set 7.

Technical Discussion¶

Important note: This condition is actually the same as the KINEMATIC condition but is applied with different numerics for special cases. Specifically, rather than treated in a Galerkin fashion, with a weighting function equal to the interpolation function for velocity, the residual equation is formed at each node directly, in a collocated fashion, without Galerkin integration. This method is better suited for high-capillary number cases in which Galerkin’s method is often not the best approach.

KINEMATIC_DISC¶

BC = KINEMATIC_DISC SS <bc_id> <float1>

Description / Usage¶

(SIC/ROTATED MESH)

This boundary condition card is used as a distinguishing condition on the mesh motion equations (viz. mesh1, mesh2, and mesh3 under the EQ card) in the special case of an interface between two fluids of different density (e.g. a gas and a liquid, both meshed up as Goma materials) through which a phase transition is occurring and there is a discontinuous velocity (see the mathematical form in the technical discussion below). Like the KINEMATIC boundary condition, it is used to distinguish a material surface between two phases exchanging mass. In two dimensions, this condition is automatically applied to the normal component of the vector mesh equations which is rotated into normal-tangential form. In three dimensions, the application of this boundary condition needs to be further directed with the ROT cards (see Rotation Specifications). The application of this condition should be compared with KINEMATIC_PETROV and KINEMATIC_COLLOC.

This condition must be applied to problem description regions using the Q1_D or Q2_D interpolation type, indicating a discontinuous variable treatment at the interface (see EQ card).

Definitions of the input parameters are as follows:

KINEMATIC_DISC	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	Set to zero for internal interfaces; otherwise used to specify the mass average velocity across the interface for external boundaries.

Examples¶

The following sample card

BC = KINEMATIC_DISC SS 10 0.0

is used at internal side set 10 (note, it is important that this side set include elements from both abutting materials) to enforce the overall conservation of mass exchange.

Technical Discussion¶

This boundary condition is typically applied to multicomponent two-phase flows that have rapid mass exchange between phases, rapid enough to induce a diffusion velocity at the interface. The best example of this is rapid evaporation of a liquid component into a gas.

This boundary condition card is used for a distinguishing condition and its functional form is:

\[\rho_1 \underline{n} \cdot \left( \underline{v} - \underline{v}_s \right) \rvert_1 = \rho_2 \underline{n} \cdot \left( \underline{v} - \underline{v}_s \right) \rvert_2\]

where 1 denotes evaluation in phase 1 and 2 denotes evaluation in phase 2.

This condition is applied to the rotated form of the mesh equations. The condition only applies to interphase mass, heat, and momentum transfer problems with discontinuous (or multivalued) variables at an interface, and it must be invoked on fields that employ the Q1_D or Q2_D interpolation functions to “tie” together or constrain the extra degrees of freedom at the interface in question (see for example boundary condition VL_EQUIL_PSEUDORXN).

References¶

GTM-015.1: Implementation Plan for Upgrading Boundary Conditions at Discontinuous-Variable Interfaces, January 8, 2001, H. K. Moffat

KINEMATIC_EDGE¶

BC = KINEMATIC_EDGE <bc_id1> <bc_id2> <float1>

Description / Usage¶

(SIC/ROTATED MESH)

This boundary condition card is used as a distinguishing condition on the mesh motion equations (viz. mesh1, mesh2, and mesh3 under the EQ card). It enforces the boundary of the mesh defined by the side set to conform to a transient or steady material surface, with an optional, pre-specified mass loss/gain rate. This condition is applied only in three-dimensional problems along contact lines that define the intersection of a freesurface and a geometrical solid, the intersection of which is partially characterized by the binormal tangent as described below.

Definitions of the input parameters are as follows:

KINEMATIC_EDGE	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id1>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain. This surface is the “primary solid surface”
<bc_id2>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain. This surface is the “free surface”
<float1>	Mass-loss (positive) or mass-gain (negative) velocity at the free boundary.

Examples¶

BC = KINEMATIC_SPECIES SS 10 2 0.0

In this example, the KINEMATIC_EDGE boundary condition is applied to the line defined by the intersection of side sets 10 and 20. The normal vector used in application of this condition is the one in the plane of side-set 10, viz. it is tangent to the surface delineated by side set 10.

Technical Discussion¶

The functional form of the kinematic boundary condition is:

\[\underline{n}_{\mathrm{cl}} \cdot \left( \underline{v} - \underline{v}_s \right) = 0\]

Here \(\underline{n}_{\mathrm{cl}}\) is the unit normal tangent vector to a line in space defined by two surfaces, in the plane of the primary surface, viz. tangent to that surface. \(\underline{v}\) is the velocity of the fluid, \(\underline{v}_s\) is the velocity of the surface (or mesh). This condition only makes sense in three dimensions, and needs to be directed with ROT conditions for proper application.

References¶

GT-007.2: Tutorial on droplet on incline problem, July 30, 1999, T. A. Baer

KINEMATIC_SPECIES¶

BC = KINEMATIC_SPECIES SS <bc_id> <integer>

Description / Usage¶

(WIC/MASS)

This boundary condition card is used to impose an interphase species flux continuity constraint on species components undergoing phase change between two materials. The species conservation equation (see EQ card and species_bulk) for a single gas or liquid phase component requires two boundary conditions because of the multivalued, discontinuous concentration at the interface. This condition should be used in conjunction with VL_EQUIL tie condition for each species. Definitions of the input parameters are as follows:

KINEMATIC_SPECIES	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer>	Species number.
<float1>	Unused floating point number.

This boundary condition is typically applied to multicomponent two-phase flows that have rapid mass exchange between phases, rapid enough to induce a diffusion velocity at the interface, and to thermal contact resistance type problems. The best example of this is rapid evaporation of a liquid component into a gas.

Examples¶

Following is a sample card:

BC = KINEMATIC_SPECIES SS 10 2 0.0

This card invokes the species flux balance condition on species 2 at shared side set 10 to be applied to the liquid phase convective diffusion equation. It should be used in conjunction with a VL_EQUIL type condition on the same species, but from the bounding phase. Note: side set 10 must be a double-sided side set between two materials (i.e., must be attached to both materials), each deploying basis function interpolation of type Q1_D or Q2_D.

Technical Discussion¶

The condition only applies to interphase mass transfer problems with discontinuous (or multivalued) variables at an interface, and it must be invoked on fields that employ the Q1_D or Q2_D interpolation functions to “tie” together or constrain the extra degrees of freedom at the interface in question. The mathematical form is

\[\underline{n} \cdot \left[ \left( \underline{v}_s - {\underline{v}}^l \right) {y_i}^l \rho^l - {\underline{j}_i}^l \right] = \underline{n} \cdot \left[ \left( \underline{v}_s - {\underline{v}}^g \right) {y_i}^g \rho^g - {\underline{j}_i}^g \right]\]

Here \({\underline{v}}^l\) and \({\underline{v}}^g\) are the gas and liquid velocity vectors at the free surface, respectively; \(\underline{v}_s\) is the mesh velocity at the same location; \(\rho^l\) and \(\rho^g\) are the liquid and gas phase densities, respectively; \({y_i}^l\) and \({y_i}^g\) are the liquid and gas phase volume fractions of component \(i\); and \({\underline{j_i}}^l\) and \({\underline{j_i}}^g\) the mass fluxes of component \(i\). This condition constrains only one of two phase concentrations at the discontinuous interface. The other needs to come from a Dirichlet boundary condition like (BC =) Y, or an equilibrium boundary condition like VL_EQUIL.

References¶

Schunk, P. R. and Rao, R. R. 1994. “Finite element analysis of multicomponent twophase flows with interphase mass and momentum transport”, Int. J. Numer. Meth. Fluids, 18, 821-842.

GTM-007.1: New Multicomponent Vapor-Liquid Equilibrium Capabilities in GOMA, December 10, 1998, A. C. Sun

KIN_DISPLACEMENT_PETROV¶

BC = KIN_DISPLACEMENT_PETROV SS <bc_id> <integer>

Description / Usage¶

(SIC/ROTATED MESH)

The KIN_DISPLACEMENT_PETROV boundary condition is exactly the same as KIN_DISPLACEMENT except in the way in which it is applied numerically to a problem. See KIN_DISPLACEMENT for a full discussion.

Definitions of the input parameters are as follows:

KIN_DISPLACEMENT_PETROV	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer>	Element block identification number for the region of TALE solid mesh motion.

Sometimes this condition is a better alternative to KIN_DISPLACEMENT to stabilize the surface and prevent wiggles. If the user wants to know more regarding numerical issues and implementation, consult the description for the fluid-counterpart KINEMATIC_PETROV card.

Examples¶

The following sample card:

BC = KIN_DISPLACEMENT_PETROV SS 7 12

leads to the application of the kinematic boundary condition (displacement form, see below) to the boundary-normal component of the mesh-stress equation to the boundary defined by side set 7. The element block ID number which shares this boundary with a neighboring TALE or fluid ARBITRARY region is 12.

Technical Discussion¶

See discussions on the KINEMATIC_PETROV and KIN_DISPLACEMENT cards.

References¶

No References.

KIN_DISPLACEMENT_COLLOC¶

BC = KIN_DISPLACEMENT_COLLOC SS <bc_id> <integer>

Description / Usage¶

(SIC/ROTATED MESH)

The KIN_DISPLACEMENT_COLLOC boundary condition is exactly the same as KIN_DISPLACEMENT except in the way in which it is applied numerically to a problem. See KIN_DISPLACEMENT for a full discussion.

Definitions of the input parameters are as follows:

KIN_DISPLACEMENT_COLLOC	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer>	Element block identification number for the region of TALE solid mesh motion.

Sometimes this condition is a better alternative to KIN_DISPLACEMENT to stabilize the surface and prevent wiggles. If the user wants to know more regarding numerical issues and implementation, consult the description for the fluid-counterpart KINEMATIC_COLLOC card.

Examples¶

The following sample card:

BC = KIN_DISPLACEMENT_COLLOC SS 7 12

leads to the application of the kinematic boundary condition (displacement form, see below) to the boundary-normal component of the mesh-stress equation to the boundary defined by side set 7. The element block ID number which shares this boundary with a neighboring TALE or fluid ARBITRARY region is 12.

Technical Discussion¶

See discussions on the KINEMATIC_COLLOC and KIN_DISPLACEMENT cards.

References¶

No References.

KIN_DISPLACEMENT¶

BC = KIN_DISPLACEMENT SS <bc_id> <integer>

Description / Usage¶

(SIC/ROTATED MESH)

This boundary condition card is used as a distinguishing condition on the mesh motion equations (viz. mesh1, mesh2, and mesh3 under the EQ card). It forces the boundary of the mesh defined by the side set to conform to a transient or steady material surface. Unlike the KINEMATIC condition, which is designed for material surfaces between two fluids, or the external material boundary of a fluid, this condition is applied to solid materials to which the TOTAL_ALE mesh motion scheme is applied (see technical discussion below and the Mesh Motion card). In two dimensions, this condition is automatically applied to the normal component of the vector mesh equations, which is rotated into normal-tangential form. In three dimensions, the application of this boundary condition needs to be further directed with the ROT cards (see ROTATION specifications). The application of this condition should be compared with KIN_DISPLACEMENT_PETROV and KIN_DISPLACEMENT_COLLOC.

Definitions of the input parameters are as follows:

KIN_DISPLACEMENT	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer>	Element block identification number for the region of TALE solid mesh motion.

Examples¶

The following sample card:

BC = KIN_DISPLACEMENT SS 7 12

leads to the application of the kinematic boundary condition (displacement form, see below) to the boundary-normal component of the mesh-stress equation to the boundary defined by side set 7. The element block ID number which shares this boundary with a neighboring TALE or fluid ARBITRARY region is 12.

Technical Discussion¶

The functional form of the kinematic boundary condition is:

Here EQUATION is the unit normal vector to the solid-fluid free surface, EQUATION is the mesh displacement at the boundary EQUATION, is the mesh displacement from the base reference state (which is automatically updated from the stress-free state coordinates and for remeshes, etc. in Goma and need not be specified), EQUATION is the real solid displacement, and EQUATION is the real solid displacement from the base reference state (or mesh). In stark contrast with the KINEMATIC condition, which too is used to distinguish a material fluid surface) this condition is written in Lagrangian displacement variables for TALE mesh motion and is applied as a distinguishing condition on the mesh between a fluid and TALE solid region. In essence, it maintains a real solid displacement field such that no real-solid mass penetrates the boundary described by this condition.

References¶

SAND2000-0807: TALE: An Arbitrary Lagrangian-Eulerian Approach to Fluid- Structure Interaction Problems, P. R. Schunk, May 2000

GT-005.3: THE NEW TOTAL-ARBITRARY-LAGRANGIAN-EULERIAN (TALE) CAPABILITY and its applicability to coating with/on deformable media, August 6, 1999, P. R. Schunk

KIN_LEAK¶

BC = KIN_LEAK SS <bc_id> <float1> <float2>

Description / Usage¶

(SIC/ROTATED MESH)

This boundary condition card is used as a distinguishing condition - kinematic with mass transfer on mesh equations. The flux quantity is specified on a per mass basis so heat and mass transfer coefficients are in units of L/t.

Definitions of the input parameters are as follows:

KIN_LEAK	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	Mass transfer coefficient for bulk fluid (species n +1).
<float2>	Driving force concentration in external phase.

Please see Technical Discussion regarding the appropriate units for the mass transfer coefficient and concentration in the external phase. For a pure liquid case, these inputs are read directly from this card, while for a multi-component case these values are read from YFLUX boundary conditions corresponding to each species that is needed. See following examples.

Examples¶

Following are two sample input cards:

Pure Liquid Case

BC = KIN_LEAK SS 3   0.1   0.

Two Component Case

BC = KIN_LEAK SS 3   0.   0.

BC = YFLUX SS 3   0   0.12   0.

Note, in the two component case, when Goma finds the KIN_LEAK card, it scans the input deck to locate the applicable YFLUX conditions associated with side set 3 and creates a linked list which is used by the applying function (kin_bc_leak). The existence of this list is denoted in Goma by the addition of an integer into an unused field of the BC structure for side set 3. The bulk fluid constitutes the second component and is non-volatile so it requires no YFLUX card; a second volatile species would require a second YFLUX input card.

Technical Discussion¶

Functionally, the KIN_LEAK boundary condition can be represented as the following:

where EQUATION is the vector velocity; EQUATION is the velocity of the boundary itself (not independent from the mesh velocity); EQUATION is the normal vector to the surface; EQUATION is the concentration of species i; EQUATION is the ambient concentration of species i at a distance from the surface of interest and EQUATION is the mass transfer coefficient for species i. This function returns a volume flux term to the equation assembly function.

KIN_LEAK is implemented through function kin_bc_leak; it sums the fluxes for all species plus the bulk phase evaporation. These fluxes are computed via several other function calls depending on the particular flux condition imposed on the boundary. (See various YFLUX * cards for Mass Equations.) However, at the end of the kin_bc_leak function, the accumulated flux value is assigned to variable vnormal, i.e., the velocity of fluid relative to the mesh. The apparent absence of a density factor here to convert a volume flux to a mass flux is the crucial element in the proper usage of the flux boundary conditions. The explanation is rooted in the formulation of the convective-diffusion equation.

The convective-diffusion equation in Goma is given as

with mass being entirely left out of the expression. J is divided by density before adding into the balance equation; this presumes that volume fraction and mass fraction are equivalent. The users must be aware of this. This formulation is certainly inconvenient for problems where volume fraction and mass fraction are not equal and multicomponent molar fluxes are active elements of an analysis. However, kin_bc_leak is entirely consistent with the convective-diffusion equation as a velocity is a volume flux, and multiplied by a density gives a proper mass flux. If y_i is a mass concentration, and h_i were in its typical velocity units, the result is a mass flux; if y_i is a volume fraction, then we have a volume flux. So kin_bc_leak is consistent.

The burden here lies with the user to be consistent with a chosen set of units. A common approach is to build density into the mass transfer coefficient h_i .

FAQs¶

See the FAQ pertaining to “Continuation Strategies for Free Surface Flows” on the DISTNG boundary condition card.
A question was raised regarding the use of volume flux in Goma; the following portion of the question and response elucidate this topic and the subject of units. Being from several emails exchanged during January 1998, the deficiencies or lack of clarity have since been remedied prior to Goma 4.0, but the discussions are relevant for each user of the code.

Question: … I know what you are calling volume flux is mass flux divided by density. The point I am trying to make is that the conservation equations in the books I am familiar with talk about mass, energy, momentum, and heat fluxes. Why do you not write your conservation equations in their naturally occurring form? If density just so happens to be common in all of the terms, then it will be obvious to the user that the problem does not depend on density. You get the same answer no matter whether you input rho=1.0 or rho=6.9834, provided of course this does not impact iterative convergence. This way, you write fluxes in terms of gradients with the transport properties (viscosity, thermal conductivity, diffusion coefficient, etc.) being in familiar units.

Answer: … First let me state the only error in the manual that exists with regard to the convection-diffusion equation (CDE) is the following:

J_i in the nomenclature table should be described as a volume flux with units of L/t, i.e., D ⋅ ∇y_i, where D is in L²/t units.

Now, this is actually stated correctly elsewhere, as it states the J_i is a diffusion flux (without being specific); to be more specific here, we should say it is a “volume flux of species i.” So, in this case D is in L ⋅ L/t units y_i, is dimensionless and it is immaterial that the CDE is multiplied by density or not, as long as density is constant.

Now, in Goma we actually code it with no densities anywhere for the FICKIAN diffusion model. For the HYDRO diffusion model, we actually compute a J_i /ρ in the code, and handle variable density changes through that ρ. In that case J_i as computed in Goma is a mass flux vector, not a volume flux vector, but by dividing it by ρ and sending it back up to the CDE it changes back into a volume flux. i. e., everything is the same.

Concerning the units of the mass transfer coefficient on the YFLUX boundary condition, the above discussion now sets those. Goma clearly needs the flux in the following form:

and dimensionally for the left hand side

where D is in units L²/t, the gradient operator has units of 1/L so K has to be in units of L/t (period!) because y_i is a fraction.

So, if you want a formulation as follows:

then K’s units will have to accommodate for the relationship between p_i and y_i in the liquid, hopefully a linear one as in Raoult’s law, i.e. if p_i = PvV_i where Pv is the vapor pressure, then

and so K on the YFLUX command has to be KPv….and so on.

Finally, you will note, since we do not multiply through by density, you will have to take care of that, i. e., in the Price paper he gives K in units of t/L. So, that must be converted as follows:

This checks out!

References¶

Price, P. E., Jr., S. Wang, I. H. Romdhane, “Extracting Effective Diffusion Parameters from Drying Experiments,” AIChE Journal, 43, 8, 1925-1934 (1997)

KIN_CHEM¶

BC = KIN_CHEM SS <bc_id> <float1> ... <floatn>

Description / Usage¶

(SIC/ROTATED MESH)

This boundary condition card is used to establish the sign of flux contributions to the overall mass balance on boundaries so that movements are appropriately advancing or receding depending on whether a species is a reactant or product in a surface reaction.

Definitions of the input parameters are as follows:

KIN_CHEM	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (set in EXODUS II) in the problem domain.
<float1>	Stoichiometric coefficient for species 0.
<floatn>	Stoichiometric coefficient for species n +1.

The input function will read as many stoichiometric coefficients as specified by the user for this card; the number of coefficients read is counted and saved. The stoichiometric coefficient is +1 for products or -1 for reactants. When a species is a product, the surface will advance corresponding to production/creation of mass of that species, versus recession of that interface when a reaction leads to consumption of that species.

Examples¶

Following is a sample card for two reactant and one product species:

BC = KIN_CHEM SS 25   -1.0   -1.0   1.0

Technical Discussion¶

This function is built from the same function as boundary condition KIN_LEAK, i.e., kin_bc_leak, so the user is referred to discussions for this boundary condition for appropriate details. The stoichiometric coefficients are read from the KIN_CHEM card or set equal to 1.0 in the absence of KIN_CHEM.

References¶

No References.

FORCE¶

BC = FORCE SS <bc_id> <float1> <float2> <float3>

Description / Usage¶

(WIC/VECTOR MESH)

This boundary condition card applies a force per unit area (traction) on a Lagrangian mesh region. The force per unit area is applied uniformly over the boundary delineated by the side set ID. The applied force is of course a vector. Definitions of the input parameters are as follows:

FORCE	Name of the boundary condition (<bc_name>)
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	X-component of traction in units of force/area.
<float2>	Y-component of traction in units of force/area.
<float3>	Z-component of traction in units of force/area.

Examples¶

Following is a sample card:

BC = FORCE SS 10 0. 1.0 1.0

This card results in a vector traction defined by EQUATION being applied to the side set boundary delineated by the number 10.

Technical Discussion¶

Important note: this boundary condition can only be applied to LAGRANGIAN, DYNAMIC_LAGRANGIAN or ARBITRARY mesh motion types (cf. Mesh Motion card). For real-solid mesh motion types, refer to FORCE_RS. Furthermore, it is rare and unlikely that this boundary condition be applied to ARBITRARY mesh motion regions. An example application of this boundary condition card is to address the need to apply some load pressure to a solid Lagrangian region, like a rubber roller, so as to squeeze and drive flow in a liquid region.

FAQs¶

On internal two-sided side sets, this boundary condition results in double the force in the same direction.

References¶

A MEMS Ejector for Printing Applications, A. Gooray, G. Roller, P. Galambos, K. Zavadil, R. Givler, F. Peter and J. Crowley, Proceedings of the Society of Imaging Science & Technology, Ft. Lauderdale FL, September 2001.

NORM_FORCE¶

BC = NORM_FORCE SS <bc_id> <float1> <float2> <float3>

Description / Usage¶

(WIC/VECTOR MESH)

This boundary condition card applies a force per unit area (traction) on a Lagrangian mesh region. The force per unit area is applied uniformly over the boundary delineated by the side set ID. The applied traction is of course a vector. Unlike the FORCE boundary condition card, the vector traction here is defined in normal-tangent vector basis. Definitions of the input parameters are as follows:

NORM_FORCE	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set.
<bc_id>	The boundary flag identifier, or a side set number which is an integer that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	Normal component of traction in units of force/area.
<float2>	Tangential component of traction in units of force/area.
<float3>	Second tangential component of traction in units of force/area (in 3-D).

This card actually applies a traction that is then naturally integrated over the entire side set of elements. Hence, the units on the floating point input must be force/area.

Examples¶

Following is a sample card:

BC = NORM_FORCE SS 10   0.   1.0   1.0

This card results in a vector traction defined by EQUATION being applied to the side set boundary delineated by the number 10. The normal vector is defined as the outward pointing normal to the surface. For internal surfaces defined by side sets which include both sides of the interface, this condition will result in exactly a zero traction, i.e., internal surface side sets must be attached to one element block only to get a net effect.

Technical Discussion¶

Important note: this boundary condition can only be applied to LAGRANGIAN, DYNAMIC_LAGRANGIAN or ARBITRARY mesh motion types (cf. Mesh Motion card). For real-solid mesh motion types, refer to NORM_FORCE_RS. Furthermore, it is rare and unlikely that this boundary condition be applied to ARBITRARY mesh motion regions. An example application of this boundary condition card is to apply some load pressure uniformly on the inside of a solid-membrane (like a pressurized balloon). In more advanced usage, one could tie this force to an augmenting condition on the pressure, as dictated by the ideal gas law.

This boundary condition is not used as often as the FORCE or FORCE_USER counterparts.

REP_FORCE¶

BC = REP_FORCE SS <bc_id> <float_list>

Description / Usage¶

(WIC/VECTOR MESH)

This boundary condition card applies a force per unit area (traction) that varies as the inverse of the fourth power of the distance from a planar surface to a Lagrangian or dynamic Lagrangian mesh region. This boundary condition can be used to impose a normal contact condition (repulsion) or attraction condition (negative force) between a planar surface and the surface of a Lagrangian region. The force per unit area is applied uniformly over the boundary delineated by the side set ID. The applied force is a vector in the normal direction to the Lagrangian interface.

Definitions of the input parameters are as follows, with <float_list> having five parameters:

REP_FORCE	Name of the boundary condition (<bc_name>)
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	Coefficient of repulsion, λ.
<float2>	Coefficient a of plane equation.
<float3>	Coefficient b of plane equation.
<float4>	Coefficient c of plane equation.
<float5>	Coefficient d of plane equation.

Refer to the Technical Discussion for an explanation of the various coefficients.

Examples¶

The following sample card:

BC = FORCE_REP SS   10  1.e+03.   1.0   0.0 0.0   -3.0

results in a vector traction of magnitude –1.0e3 ⁄ h⁴ in the normal direction to surface side set 10 and the distance h is measured from side set 10 to the plane defined by 1.0x – 3. = 0.

Technical Discussion¶

The REP_FORCE boundary condition produces a vector traction in the normal direction to a surface side set, defined by:

where F is a force per unit area that varies with the distance h from a plane defined by

The normal vector is defined as the outward pointing normal to the surface. For internal surfaces defined by side sets which include both sides of the interface, this condition will result in exactly a zero traction, i.e., internal surface side sets must be attached to one element block only to get a net effect.

Important note: this boundary condition can only be applied to LAGRANGIAN, DYNAMIC_LAGRANGIAN or ARBITRARY mesh motion types (cf. Mesh Motion card). For real-solid mesh motion types, refer to REP_FORCE_RS. Furthermore, it is rare and unlikely that this boundary condition be applied to ARBITRARY mesh motion regions. An example application of this boundary condition card is to apply some load pressure uniformly on a surface that is large enough such that this surface never penetrates a predefined planar boundary. Hence, this condition can be use to impose an impenetrable contact condition.

FAQs¶

On internal two-sided side sets, this boundary condition results in double the force in the same direction.

FORCE_USER¶

BC = FORCE_USER SS <bc_id> <float1> ...<floatn>

Description / Usage¶

(WIC/VECTOR MESH)

This boundary condition card applies a user-defined force per unit area (traction) on a Lagrangian or dynamic Lagrangian (see Mesh Motion card) mesh region. The functional form of the force is programmed in the function force_user_surf in bc_user.c, and can be made a function of any of the independent or dependent variables of the problem, including position (see example below). The force per unit area is applied to boundary delineated by the side set ID. Definitions of the input parameters are as follows:

FORCE_USR	Name of the boundary condition (<bc_name>)
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>…<floatn>	Parameters list (length arbitrary) for parameterizing the user defined force. These parameters are accessed through the p[]array in force_user_surf.

Examples¶

The input card

BC = FORCE_USER SS 3   {delta_t} 0.   1000.0 0.

used in conjuction with the following snippet of code in force_user_surf:

/* Comment this out FIRST!!!!! */
   /* EH(-1,"No FORCE_USER model implemented"); */
   /**************************** EXECUTION BEGINS
   *******************************/
   if (time <= p[0])
   {
           func[0] = p[1]*time/p[0];
           func[1] = p[2]*time/p[0];
           func[2] = p[3]*time/p[0];
   }
   else
   {
           func[0] = p[1];
           func[1] = p[2];
           func[2] = p[3];
   }

applies a time-dependent force ramped from zero to 1000.0 in the +y direction over the time period {delta_t}.

Technical Discussion¶

Used commonly to apply a force per unit area to an external surface of a solid region (LAGRANGIAN type, cf. FORCE_USER_RS), that is nonconstant, viz. time varying or spatially varying. The FORCE and NORM_FORCE boundary conditions can be used for constant forces. This condition is applied as a weak integrated condition in Goma, and hence will be additive with others of its kind.

FAQs¶

On internal two-sided side sets, this boundary condition results in double the force in the same direction.

References¶

No References.

CA¶

BC = CA NS <bc_id> <float_list>

Description / Usage¶

(PCC/ROTATED MESH)

This boundary condition card applies a specified contact-angle on the mesh at a single node nodeset. It is used exclusively in two dimensional computations. Its primary application is imposing contact angles at static or dynamic contact lines. Consequently, the nodeset is usually found where a free-surface boundary intersects a fixed, “geometry” boundary.

The <float_list> for this boundary condition has four values; definitions of the input parameters are as follows:

CA	Name of the boundary condition.
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	θ, angle subtended by wall normal and free surface normal, in units of radians.
<float2>	n_x, x-component of normal vector to the geometry boundary (see important note below regarding variable wall normals, viz. non-planar solid walls).
<float3>	n_y, y-component of normal vector to the geometry boundary. (see important note below regarding variable wall normals, viz. non-planar solid walls).
<float4>	n_z, z-component of normal vector to the geometry boundary. (see important note below regarding variable wall normals, viz. non-planar solid walls).

Examples¶

Following is a sample card:

BC = CA NS 100 1.4 0. 1. 0.

This condition applies a contact angle of 1.4 radians between the free surface normal at the 100 nodeset and the vector (0,1,0). Normally, this latter vector is the normal to the solid surface in contact with the free surface at this point.

Technical Discussion¶

The constraint that is imposed at the nodeset node is:

where n is the normal to the geometry specified on the card itself, and n_fs is the normal to the outward free surface computed internally by Goma. Also see the CA_OR_FIX card for an extension to this condition and CA_EDGE for its extension to three dimensions.
In addition for the case in which the geometry normal components are set to zero, the wall normal is allowed to vary with a geometrical boundary condition, i.e., GD_TABLE, SPLINE, PLANE, etc. The geometry normal is found on the same or on a neighboring element that contains the dynamic contact angle in question. If a GD*_ type boundary condition is used to describe the wall (i.e., *GD_TABLE), one must specify the R_MESH_NORMAL equation type on that equation for the variable wall normal to take effect.
Important: Variable Wall Normals. Situations for which the wall shape is nonplanar, meaning that the normal vector is not invariant as the contact line moves, there is an option to leave all of the normal-vector components zero. In this case Goma then seeks to determine the local wall normal vector from the geometry it is currently on, using the element facets. It is recommended that this option not be used unless the geometry is truly nonplanar, as the logic is complex and not 100% reliable. An example of such a case is as follows:

BC = CA NS 100 1.4 0. 0. 0.

Notice how all three components of the normal vector are set to zero.

Important: Wall Normal convention. The wall normal vector on an external solid boundary is defined in goma as the inward facing normal to the mesh, and the free surface normal to the liquid (or wetting phase for two-liquid systems) is defined as the outward facing normal to the free surface. Put another way and referring to the picture below, the wall normal is directed from the “solid phase” to the “liquid phase”, and the free surface normal is directed from the “liquid phase” or “wetting phase” to the “vapor phase” or “Non-wetting phase”. Note that for zero contact angle the liquid is “perfectly wetting”. The air-entrainment limit (viz. the hydrodynamic theory interpretation) would occure at a 180 degree contact angle. Recall that the angle is specified in radians on this card.

References¶

No References.

CA_OR_FIX¶

BC = CA_OR_FIX NS <bc_id> <float_list>

Description / Usage¶

(PCC/ROTATED MESH)

This boundary condition card allows the application of Gibb’s inequality condition in conjuction with a contact angle. This allows for a point to be specified at which a contact line will attach itself and no longer move. Up to that point, the contact line will advance or recede with a specified fixed contact angle. When the contact line attaches, its contact angle is allowed to vary permitting the user to include discontinuities in surface slope as features of the problem. The Gibb’s condition also permits the contact line to detach from its fixed point if the contact angle enters a certain range after attaching. This boundary condition is applicable only to two-dimensional problems; see CA_EDGE_OR_FIX for details on three dimensional implementations.

The <float_list> has seven values, with definition of the input parameters as follows:

CA_OR_FIX	Name of the boundary condition.
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	θ_dcl, dynamic contact angle, in radians.
<float2>	n_x, x-component of outward-pointing wall surface normal.
<float3>	n_y, y-component of outward-pointing wall surface normal.
<float4>	n_z, z-component of outward-pointing wall surface normal.
<float5>	x₀, x-coordinate of the point or feature at which the meniscus will pin.
<float6>	y₀, y-coordinate of the point or feature at which the meniscus will pin.
<float7>	z₀, z-coordinate of the point or feature at which the meniscus will pin.

Examples¶

Following is a sample card:

BC = CA_OR_FIX NS 100 1.3 0. 1. 0. -0.5 1. 0.

Technical Discussion¶

The Gibb’s inequality condition is illustrated in the accompanying figure. The fixed point is indicated by the plane, x = x₀. Initially, the contact line is far from this point as the condition at the contact line fixes the contact angle to the value θ_dcl. However, when the contact line approaches to within ε (1.e-6) of the fixed point, it attaches there and stops moving. The contact angle condition is no longer enforced and the angle of the free surface with respect to the solid normal vector is allowed to vary freely. The other part of the Gibb’s inequality is illustrated (above) by the last sketch. Here, by virture of the overall fluid mechanics, the contact angle withdraws until it is larger than θ_dcl. When this happens the contact line is no longer affixed at x = x₀ and is allowed to move freely. Once again the contact angle condition is enforced.

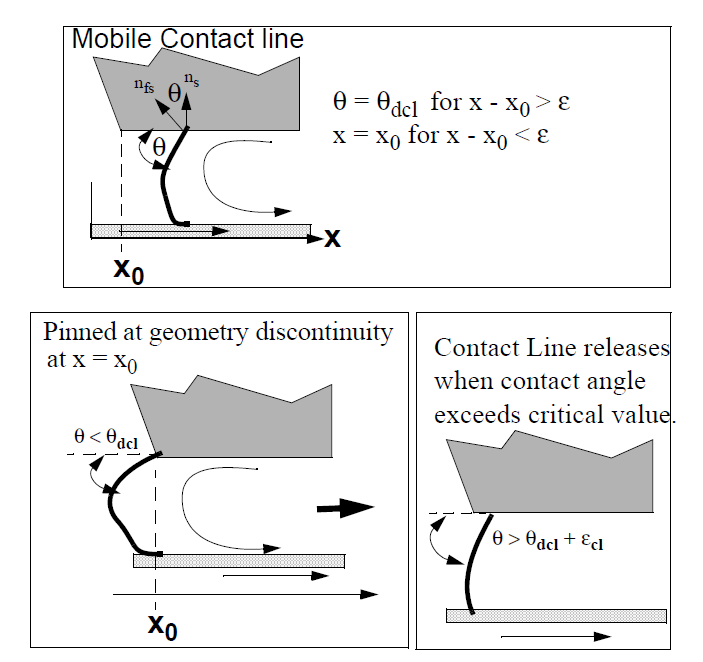
Contact angles and Gibb’s inequality condition in Goma, for the special case when the meniscus is moving along a surface of constant x.¶

Also, please see the important note under the BC = CA card regarding the convention used for specifying wall and free surface normal vectors.

Theory¶

The principle behind this condition applies when a contact line encounters a sharp feature on a surface. The feature from a distance might appear as a sharp corner at which the meniscus/contact line prefers to locate rather than undergo continued migration. Actually on a smaller scale, the corner feature is not infinitely small, and the contact line undergoes no perceptable movement on the macroscale in order to satisfy a true contact angle. Rather than resolving this feature with a fine mesh, it is an expedient to pin the contact line there and allow it to take on any macroscale contact angle within a certain range. The line can release again if the meniscus pulls the contact line sufficiently to overcome specified bounds.

References¶

No References.

CA_EDGE¶

BC = CA_EDGE SS <bc_id1> <bc_id2> <float_list>

Description / Usage¶

(PCC-EDGE/ROTATED MESH)

This boundary condition card specifies a constant contact angle on the edge defined by the intersection of the primary and secondary side sets. This card is used most often to enforce contact angle conditions on three-dimensional static contact lines. It should not be used in two-dimensional problems, where the CA boundary condition is the appropriate choice.

The contact angle supplied on the card will be enforced so that it is the angle between the outward-pointing normal of the primary side set and the unit vector supplied on the card. It is important to note that this outward-pointing normal should be variable, that is to say, the primary side set is most likely a free-surface.

Definitions of the input parameters are as follows:

CA_EDGE	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id1>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain. This identifies the primary side set; in almost all cases it should also be a free surface.
<bc_id2>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain. This identifies the secondary side set, which plays no other role in this boundary condition than to provide a means of defining the appropriate edge geometry in conjunction with the primary side set. Thus, the secondary side set will often represent a solid boundary.
<float1>	angle, value specifying the enforced angle, in degrees; it should lie in the range 0 ≤ angle ≤ 180.
<float2>	n_x, the x-component of the fixed unit vector.
<float3>	n_y, the y-component of the fixed unit vector.
<float4>	n_z, the z-component of the fixed unit vector.

This boundary condition is a point collocated condition so it will be enforced exactly at every node that lies on the edge (subject to overriding ROT cards or Dirichlet conditions).

Examples¶

The following is a sample input card:

BC = CA_EDGE SS 40 50 33.0 0. 1. 0.

This card will result in an angle of 33 degrees between the outward-pointing normal to side set 40 and the vector (0,1,0) at all points on the edge defined by the intersection of side set 40 and side set 50.

Technical Discussion¶

Although this constraint deals with vector quantities, it is a scalar constraint. The actual requirement that is imposed is:

where n_f is the outward-pointing normal to the primary side set, n is the vector supplied on the card, and θ is the angle supplied on the card. It should be recognized that there are usually two orientations for n_f which would satisfy this constraint. Most often the surrounding physics will choose the correct one, but there is nothing to guarantee this in special situations, for example, values for θ near zero or near 180.

This boundary condition is a point collocated condition so the preceding constraint, will be enforce exactly and strongly for each node on the edge. The actual free surface normal is an average of vectors supplied by adjacent elements sharing a given node.
As noted above, this boundary condition is most often used in three-dimensional free surface problems to enforce static contact angle conditions at the junction of a free, capillary surface and a solid boundary. The normal vector supplied on the card would be the normal to this solid boundary. Since this vector is a constant, there is the restriction that in this application this boundary condition can only be used to specify a contact angle with respect to a planar solid boundary. A different boundary condition, CA_EDGE_CURVE, should be used if the solid boundary is not planar.
Related boundary conditions: CA_EDGE_INT, CA_EDGE_CURVE, CA_EDGE_CURVE_INT, VAR_CA_EDGE, VAR_CA_USER.

References¶

No References.

CA_EDGE_INT¶

BC = CA_EDGE_INT SS <bc_id1> <bc_id2> <float_list>

Description / Usage¶

(SIC-EDGE/ROTATED MESH)

This boundary condition card specifies a constant contact angle on the edge defined by the intersection of the primary and secondary side sets. It is identical in format and function as the CA_EDGE boundary condition. The only difference is that this boundary condition is a strong integrated constraint.

Definitions of the input parameters are as follows:

CA_EDGE_INT	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id1>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain. This identifies the primary side set; in almost all cases it should also be a free surface.
<bc_id2>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain. This identifies the secondary side set, which plays no other role in this boundary condition than to provide a means of defining the appropriate edge geometry in conjunction with the primary side set. Thus, the secondary side set will often represent a solid boundary.
<float1>	angle, value specifying the enforced angle, in degrees; it should lie in the range 0 ≤ angle ≤ 180.
<float2>	n_x, the x-component of the fixed unit vector.
<float3>	n_y, the y-component of the fixed unit vector.
<float4>	n_z, the z-component of the fixed unit vector.

Examples¶

The following is a sample input card:

BC = CA_EDGE_INT SS 40 50 33.0 0. 1. 0.

This card will result in an angle of 33 degrees between the outward-pointing normal to side set 40 and the vector (0,1,0) at all points on the edge defined by the intersection of side set 40 and side set 50.

Technical Discussion¶

As noted above, this boundary condition is identical in function to the CA_EDGE condition. It differs only in the manner of its application. Whereas, the former was a point collocated constraint, this boundary condition strongly enforces the following integrated constraint at a node i**:

where φ_i is the finite element trial function for node i, Γ is the edge space curve, n:sub: f is the outward-pointing normal to the primary sideset, n is the vector supplied on the card, and θ is the angle supplied on the card. Because it is an integrated constraint, evaluation of the free-surface normal vector is done at integration points between nodes on the edge. Therefore, there is no averaging of normal vectors. This is sometimes advantageous when there are discontinuities in the slope of the edge curve.

Related boundary conditions: CA_EDGE, CA_EDGE_CURVE, CA_EDGE_CURVE_INT, VAR_CA_EDGE, VAR_CA_USER.

References¶

No References.

CA_EDGE_OR_FIX¶

BC = CA_EDGE_OR_FIX SS <bc_id1> <bc_id2> <type_string> {float_list}

Description / Usage¶

(PCC/ROTATED MESH)

In analogy to the two-dimensional condition, CA_OR_FIX, boundary condition, this boundary condition imposes a contact angle on an edge feature in a three-dimensional mesh. However, this condition also permits the user to specify a closed curve on the substrate plane on which the contact line will attach and not move past. This permits modeling of geometric features in which the substrate slope is discontinuous. When contact lines encounter such sharp features, usually they arrest. The boundary condition also permits the contact line to release from the curve if the overall fluid mechanics would promote a recession of the contact line.

Description of the card parameters is as follows:

CA_EDGE_OR_FIX	Name of boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id1>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain. This identifies the primary side set defining the edge curve on which this condition applies.
<bc_id2>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain. This identifies the secondary side set defining the edge curve on which this condition applies. Taken together, the edge curve is the intersection of the primary and secondary sidesets.
<type_string>	A string identifying the type of feature curve being defined; currently, there are only two choices: CIRCLE and USER. The CIRCLE options indicates that the surface feature on which a Gibb’s criterion is applied is a circle in the substrate plane. The USER option indicates that the user will have to provide a geometric definition in the user subroutine user_gibbs_criterion in the file user_bc.c.
{float_list}	A list of float parameters to be used in defining the contact angle, the normal to the substrate, and other geometric parameters used to define the feature curve. For each <type_string> choice there is a different set of float parameters:
	CIRCLE <float_list>
	<float1>	θ_dcl, contact angle at dynamic contact line, in radians
	<float2>	n_x, x-component of outward substrate normal
	<float3>	n_y, y-component of outward substrate normal
	<float4>	n_z, z-component of outward substrate normal
	<float5>	c_x, x coordinate of circle center
	<float6>	c_y, y-coordinate of circle center
	<float7>	c_z, z-coordinate of circle center
	<float8>	r, radius of circle
	The sign of this last parameter is important. If negative, the implication is that the starting location of the contact line is outside of the circle. If positive, the original location is assumed to be completely inside the circle.
	USER <float_list>
	<floati>	a list of float values that are passed to the function user_gibbs_criterion in the one-dimensional array p in the order in which they appear on the card from left to right. The user must be certain that the parameters appearing here are sufficient for applying the Gibbs criterion as well as imposing the appropriate contact angle.

Examples¶

An example making use of the CIRCLE feature curve option is as follows:

BC = CA_EDGE_OR_FIX SS 10 20 CIRCLE 1.3   0. -1. 0.   0. 0. 0.   1.0

This card applies to the intersection between side sets 10 and 20. The constant contact angle applied is 1.3 radians. The substrate outward normal is (0, -1, 0). The feature is a circle of radius 1.0 centered at (0.0, 0.0, 0.0). The original location for the contact line must be completely inside of the feature circle. Note also that the circle center should lie in the substrate plane.

Technical Discussion¶

See the Technical Discussion under the boundary condition CA_OR_FIX for a detailed discussion of the nature of the Gibb’s criterion as it applies to contact lines. In a nutshell, however, the basic notion is that the contact line is free to advance over the substrate with an imposed contact angle, constant or dependent on the local conditions. When the contact angle encounters the geometric feature defined in the function user_gibbs_criterion, it is captured at that point and no longer advances. The contact angle is allowed to vary as long as it is held at the feature. The boundary condition also permits the contact line to release from the feature curve and recede the way it came if the contact angle ever becomes larger than its mobile value.
So the phenomena that can be modeled with this boundary condition are those in which a contact line moves to, for example, the edge of cylinder. At the edge, the very small curvature of this feature effectively presents a barrier to further advance of the contact line provided the deformation of the free surface beyond the vertical boundaries of the cylinder is not too large. In the fullness of time, it might also be the case that the free surface is drawn backwards in the direction of the cylinder axis. The contact line should also recede and this boundary condition permits this once the contact angle it makes with the cylinder top exceeds the mobile contact angle by a small amount.

References¶

No References.

CA_EDGE_CURVE¶

BC = CA_EDGE_CURVE SS <bc_id1> <bc_id2> <float1>

Description / Usage¶

(PCC-EDGE/ROTATED MESH)

This boundary condition allows the user to specify a constant contact angle along an edge in three-dimensions. It is similar in function to the CA_EDGE boundary condition in which the contact angle is enforced with respect to a fixed vector. However, for this boundary condition, the contact angle is enforced with respect to the normal of the secondary side set thereby permitting a contact angle constraint to be applied on a curving surface. The boundary condition is applied to the edge curve defined by the intersection of the primary and secondary side sets.

Definitions of the input parameters are as follows:

CA_EDGE_CURVE	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id1>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain. This identifies the primary side set; in almost all cases it should also be a free surface.
<bc_id2>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain. This identifies the secondary side set. The outwards-pointing normal vector to this side set is used as the substrate vector when enforcing the contact angle constraint.
<float1>	the enforced contact angle, in degrees. Its value should lie in the range 0 ≤ angle ≤ 180.

Examples¶

The following is a sample input card:

BC = CA_EDGE_CURVE SS 40 50 135.0

This boundary condition will enforce a 135 degree angle between the normal to the free surface on side set 40 and the outward-pointing normal to side set 50 at all points along the edge defined by side set 40 and 50. There is no restriction on whether side set 50’s normal vectors must be constant.

Technical Discussion¶

Although this boundary condition deals with vector quantities it is a scalar constraint. The actual requirement that is imposed is:

where n_f is the outward-pointing normal to the primary side set, n_s is the outward-pointing normal to the secondary side set, and θ is the angle supplied on the card. There is always some confusion regarding the sense of the angle; use the figure to the right for guidance. Note that the sense depicted here is at odds with the usual contact angle convention. Keep this in mind when using this card.
As in the case of the CA_EDGE condition, this condition is also a strongly enforced point collocated condition.
Related boundary conditions: CA_EDGE, CA_EDGE_INT, CA_EDGE_CURVE_INT, VAR_CA_EDGE, VAR_CA_USER.

References¶

No References.

CA_EDGE_CURVE_INT¶

BC = CA_EDGE_CURVE_INT SS <bc_id1> <bc_id2> <float1>

Description / Usage¶

(SIC/ROTATED MESH)

This boundary condition allows the user to specify a constant contact angle along an edge in three-dimensions. It is identical in function to CA_EDGE_CURVE boundary condition, but applies as a strongly integrated constraint. The boundary condition is applied to the edge curve defined by the intersection of the primary and secondary side sets.

Definitions of the input parameters are as follows:

CA_EDGE_CURVE_INT	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id1>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain. This identifies the primary side set; in almost all cases it should also be a free-surface.
<bc_id2>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain. This identifies the secondary side set. The outwards-pointing normal vector to this side set is used as the substrate vector when enforcing the contact angle constraint.
<float1>	the enforced contact angle, in degrees. Its value should lie in the range 0 ≤ angle ≤ 180.

Examples¶

The following is a sample input card:

BC = CA_EDGE_CURVE_INT SS 40 50 135.0

This boundary condition will enforce a 135 degree angle between the normal to the free surface on side set 40 and the outward-pointing normal to side set 50 at all points along the edge defined by side set 40 and 50. The is no restriction on whether side set 50’s normal vectors must be constant.

Technical Discussion¶

Although this boundary condition deals with vector quantities it is a scalar constraint. As noted above the form of the constraint is identical to that in the CA_EDGE_CURVE boundary. In this case, it is applied as a strong integrated constraint:

where φ_i is the finite element trial function for node i, Γ is the edge space curve, n_f is the outwardpointing normal to the primary sideset, n_s is the outward-pointing normal to the secondary sideset, and θ is the angle supplied on the card. There is always some confusion regarding the sense of the angle. Use the figure to the right for guidance. Note that the sense depicted here is at odds with the usual contact angle convention. Keep this in mind when using this card.
As in the case of the CA_EDGE_INT condition, this condition is also a strongly integrated constraint.
Related boundary conditions: CA_EDGE, CA_EDGE_INT, CA_EDGE_CURVE, VAR_CA_EDGE, VAR_CA_USER.

References¶

No References.

VAR_CA_EDGE¶

BC = VAR_ CA_EDGE SS <bc_id1> <bc_id2> <float_list>

Description / Usage¶

(SIC-EDGE/ROTATED MESH)

This card is used to set a variable contact angle on a dynamic three-dimensional contact line. A local contact angle is determined based upon the local rate of advance/recession of the contact line with respect to a web, and is always associated with the secondary sideset. This card specifies the static contact angle, θ_s, and a linear proportionality constant c_T between the local advance/recession rate and the cosine of the contact angle. The speed of the moving web is specified by components of the web velocity. The contact angle is imposed between the outward-pointing normal of the primary sideset and the outward-pointing normal of the secondary sideset.

Definitions of the input parameters are as follows:

VAR_CA_EDGE	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id1>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain. This identifies the primary side set; it should be a free surface.
<bc_id2>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain. This identifies the secondary side set, which should be a “fixed” geometric entity, e.g. PLANE or SPLINE. Taken together, the primary and secondary sidesets define an edge over which this boundary is applicable.
<float1>	θ_s, parameter that is the static contact angle, in degrees. This is the contact angle that the fluid approaches when the relative motion of the contact line and substrate is zero.
<float2>	c_T, parameter that is the linear proportionality constant between the local advance/recession rate and the cosine of the contact angle; see details below in the Technical Discussion.
<float3>	W_x, x-component of the substrate velocity.
<float4>	W_y, y-component of the substrate velocity.
<float5>	W_z, z-component of the substrate velocity.

Examples¶

The following is a sample input card:

BC = VAR_CA_EDGE SS 60 20   135. 0.02   0. -1. 0.

This card sets a variable contact angle condition on the edge between side sets 60 and 20. The static contact angle is 135 degrees and the slope parameter is 0.02. The solid substrate is moving at the fixed velocity (0, -1., 0.).

Technical Discussion¶

A contact line that moves relative to its underlying solid substrate is referred to as a dynamic contact line. For a dynamic contact line associated with threedimensional flows, it is recognized that the dynamic contact angle must change from point to point along the curve because the local advance/recession rate of the contact line with respect to the substrate changes. Taking this variability into account is the function of this card.

To understand the function of this card, we first define that the advance (or recession) rate of the contact line, u_wet, as the normal component of the contact line velocity, x_cl , relative to the substrate velocity, W:

where n_cl is a unit vector normal to the contact line in the plane of the substrate as illustrated in the sketch at right. For an advancing contact line u_wet is negative and the converse. We can also define a local capillary number by nondimensionalizing the advance rate as follows,

where μ is the viscosity and σ the surface tension.

We choose to define the contact angle as the angle between the outward normal to the free-surface and the substrate normal pointing away from the fluid phase as illustrate here. From direct observation of contact lines, we know that increasing the advance rate will decrease the contact angle towards zero. Conversely, a decrease in the advance rate or increase of recession rate will increase the contact angle towards 180. We capture the essence of this behavior via a simple linear relationship between the local capillary number and the cosine of the contact angle:

where θ_s and c_T are two input parameters. The function of this card is to apply this model for contact angle on the contact line curve.

This model has many restrictions. It is really only valid for very very small | Ca_L | and also does not predict that the contact angle asymptotically approaches 0 or 180 for | Ca_L | very large. Instead, it is algorithmically restricted to returning 0 or 180 if the above linear relation would predict an angle outside of these bounds.
Unlike the CA_EDGE boundary condition, the VAR_CA_EDGE condition is applied as a strong integrated constraint. The equation associated with each node on the edge is:

where φ_i is the shape function associated with node i.

References¶

No References.

VAR_CA_USER¶

BC = VAR_CA_USER SS <bc_id1> <bc_id2> <float_list>

Description / Usage¶

(SIC-EDGE/ROTATED MESH)

This card is used to set a variable contact angle on a dynamic three-dimensional contact line. It is identical in function to the VAR_CA_USER except that it allows the user to provide a contact angle model to relate local contact angle to local capillary number.

Definitions of the input parameters are as follows:

VAR_CA_USER	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id1>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain. This identifies the primary side set; it should be a free surface.
<bc_id2>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain. This identifies the secondary side set, which should be a “fixed” geometric entity, e.g. PLANE or SPLINE. Taken together, the primary and secondary sidesets define an edge over which this boundary is applicable.
<float1>	W_x, x-component of the substrate velocity.
<float2>	W_y, y-component of the substrate velocity.
<float3>	W_z, z-component of the substrate velocity.
[float4-floatn]	An optional list of floats which will be passed to the user-supplied function for use with the user model.

Examples¶

The following is a sample input card:

BC = VAR_CA_USER SS 60 20   -1. 0. 0. 1.e-3 135.0

This card sets a variable contact angle condition on the edge between side sets 60 and 20. The solid substrate is moving at the fixed velocity (-1., 0., 0.). The var_CA_user function is passed the constants 1.e-3 and 135.0 in variable locations p[0] and p[1], respectively.

Technical Discussion¶

VAR_CA_USER function is identical to VAR_CA_EDGE. It is applied to threedimensional dynamic contact lines in order to set a variable contact angle. The user must supply internal coding for the function var_CA_user in the file user*_bc.c. This function receives as parameters the local capillary number as described under *VAR_CA_EDGE and a double array containing the optional list of float parameters. It should return the cosine of the desired contact angle.
What follows is an example that implements the linear contact angle model described in VAR_CA_EDGE.

 double
 var_CA_user(double Ca_local,
            int num,
            const double *a,
            double *d_cos_CA_Ca_local)
{
 double cos_CA;
 double static_CA;
 double cT;
 static_CA = a[0]*M_PIE/180.0;
 cT = a[1];
 cos_CA = cos(static_CA) - cT * Ca_local;
 *d_cos_CA_Ca_local = cT;
 return ( cos_CA );
}

References¶

No References.

FRICTION¶

BC = FRICTION SS <bc_id> <float1> [integer1]>

Description / Usage¶

(WIC/VECTOR MESH)

This boundary condition card applies a force per unit area (traction) on a Lagrangian mesh region. The force per unit area is applied according to Coulomb’s friction law over the boundary delineated by the side set ID. The applied traction is of course a vector. The vector traction is defined in normal-tangent vector basis. Definitions of the input parameters are as follows:

FRICTION	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set.
<bc_id>	The boundary flag identifier, or a side set number which is an integer that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	\(\mu\), Coulombic coefficient of friction.
[integer1]	optional specification of the element block id to which this condition will be applied.

This card actually applies a traction that is then naturally integrated over the entire side set of elements.

Examples¶

Following is a sample card:

BC = FRICTION SS 10 0.1 2

Technical Discussion¶

Important note: this boundary condition can only be applied to LAGRANGIAN, DYNAMIC_LAGRANGIAN or ARBITRARY mesh motion types (cf. Mesh Motion card). For real-solid mesh motion types, refer to FRICTION_RS.

This condition should be utilized in conjunction with a rotated condition such as SPLINE in order to apply a tangential force which is proportional to the normal force;

where \(\mu\) is the coefficient of friction and \(\underline{v}\) is the velocity of the convected solid. Note that the direction of the frictional force is determined by the velocity direction.

SOLID_FLUID¶

BC = SOLID_FLUID SS <bc_id> <integer1> <integer2> [float]

Description / Usage¶

(PCC/VECTOR REALSOLID)

The SOLID_FLUID condition performs the exact same task as the FLUID_SOLID condition. The usage and example are also the same, so consult the discussion on that card for further information.

At one time this condition applied the stress balance between solid and fluid phases in a different fashion that proved not to be useful. To preserve backward compatibility, we have kept this boundary condition around even though it invokes the exact same function that the FLUID_SOLID boundary condition does.

Definitions of the input parameters are as follows:

SOLID_FLUID	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer1>	Element block ID of solid phase from the EXODUS II database.
<integer2>	Element block ID of liquid phase from the EXODUS II database.
[float]	Scale factor for stress balance for non-dimensionalization. This parameter, which multiplies the liquid phase contribution of stress, is optional. The default is 1.0.

Examples¶

See FLUID_SOLID description.

Technical Discussion¶

See FLUID_SOLID description.

References¶

No References.

PENETRATION¶

BC = PENETRATION

Description / Usage¶

()

No longer supported/used in Goma. See DARCY_CONTINUOUS boundary condition card.

Examples¶

No Example.

Technical Discussion¶

No Discussion.

References¶

No References.

POROUS_KIN¶

BC = POROUS_KIN

Description / Usage¶

()

This boundary condition card was used as a distinguishing condition for the Darcy- Flow in porous medium, in an arbitrary frame of reference.

This boundary condition was disabled in November of 2001 due to the new formulation in Goma for poroelasticity; this boundary condition was poorly formulated.

Examples¶

No Example.

Technical Discussion¶

No Discussion.

References¶

No References.

SDC_KIN_SF¶

BC = SDC_KIN_SF SS <bc_id> <integer> {char_string}

Description / Usage¶

(SIC/ROTATED MESH)

This boundary condition represents the specification of the normal component of the mesh velocity. This is a DVI_MULTI_PHASE_SINGLE boundary condition that has an additional property. The first time encountered in the formation of the residual, the results of a subcalculation are stored either at the node structure level or at the surface gauss point level. The surface reaction and surface species are specified as part of a surface domain within Chemkin.

The SURFDOMAINCHEMKIN_KIN_STEFAN_FLOW boundary condition (shortened to SDC_KIN_SF in the name2 member of the BC_descriptions struct in mm_names.h) solves the following equation representing Stefan flow at a boundary.

where \(n_1\) is the outward facing normal to the liquid material, \(p^1\) is the liquid density, \(u^1\) is the (mass average) velocity at the current surface quadrature point, and \(u_s\) the velocity of the mesh (i.e., the interface if the mesh is fixed at the interface). The summation over N species is for the product of molecular weight ( \(W_k\) ) and the source term for creation of species k in the liquid ( \(S^1_k\) ). SDC_KIN_SF is linked to the SDC_SPECIES_RXN boundary conditions just as the KINEMATIC_CHEM boundary conditions are by the expression for the interface reaction. The sum is over all of the interfacial source terms for species in the phase.

Definitions of the input parameters are as follows:

SDC_KIN_SF	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer>	lement Block ID of the phase on whose side of the interface this boundary condition will be applied.
char_string	\(S^1_k\) string indicating where the surface source term information for this boundary condition will be obtained. Three options exist: IS_EQUIL_PSEUDORXN VL_EQUIL_PSEUDORXN SDC_SURFRXN These are boundary conditions that apply to the Species Equations. The last boundary condition is not yet implemented, so SDC_SURFRXN currently does nothing.

Examples¶

Following is a sample card:

BC = SDC_KIN_SF SS 1   0 VL_EQUIL_PSEUDORXN

The above card will create a strongly integrated boundary condition specifying the normal component of the velocity on side set 1 on the element block 0 side of the interface. The source term to be used in the above equation will be taken from multiple previously specified multiple VL_EQUIL_PSEUDORXN cards.

Technical Discussion¶

This boundary condition is exactly the same as SDC_STEFANFLOW, except for the fact that it is applied on the normal component of the mesh velocity instead of the normal component of the mass averaged velocity. It is similar to a single phase boundary condition, because all of its input comes from one side of the interface. Thus, it can equally be applied to external surfaces as well as internal ones with some development work.
Currently, it has only been tested out on internal boundaries using the IS_EQUIL_PSEUDORXN source term.
The DVI_MULTI_PHASE_SINGLE variable is a nomenclature adopted by Moffat (2001) in his development of a revised discontinuous variable implementation for Goma. It pertains to Discontinuous Variable Interfaces (DVI) and boundary conditions that involve the addition of a surface integral to each side of an internal boundary for a variable that is continuous across the interface. The user is referred to Moffat (2001) for detailed presentation on discontinuous variables.

References¶

GTM-015.1: Implementation Plan for Upgrading Boundary Conditions at Discontinuous-Variable Interfaces, January 8, 2001, H. K. Moffat

Category 3: Real Solid Equations¶

The reader is referred to a report by Schunk (2000) for a complete description of this equation type. Briefly, these boundary conditions pertain to the TOTAL_ALE mesh motion type (see Mesh Motion card), and are applied to the real solid only, viz. the boundary conditions applied to the companion mesh motion equations are still needed to control the mesh, independent of the realsolid material.

DXDYDZ_RS¶

BC = {DX_RS | DY_RS | DZ_RS} NS <bc_id> <float1> [float2]

Description / Usage¶

(DC/REALSOLID)

This boundary condition format is used to set a constant X, Y, or Z real-solid displacement on the real-solid mesh motion equations (see TOTAL_ALE option on the Mesh Motion card). Each such specification is made on a separate input card. These boundary conditions are of the Dirichlet type and must be applied on EXODUS II node sets. Definitions of the input parameters are as follows:

{DX_RS \| DY_RS \| DZ_RS}	Boundary condition name (<bc_name>) that defines the displacement, where: DX_RS - real solid X displacement DY_RS - real solid Y displacement DZ_RS - real solid Z displacement
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	Value of the real_solid displacement (X, Y, or Z) defined above.
[float2]	An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

Following is a sample card which applies in an X-displacement boundary condition to the real-solid to the nodes in node set 100, specifically an X- real-solid Displacement of 0.1. These displacements are applied immediately to the unknowns, and hence result in immediate mesh displacement from the initial state.

BC = DX_RS NS 100 1.0

This sample card applies the same condition above, but as a residual equation that is iterated upon with Newton’s method.

BC = DX_RS NS 100 1.0   1.0

The second float 1.0 forces this application. This approach is advisable in most situations, as the nodes are gradually moved as a part of the mesh deformation process. Sudden movements, as in the first example, can lead to folds in the mesh.

Technical Discussion¶

This condition performs the same function as DX|DY|DZ boundary conditions, except that it is applied to the real-solid of a TOTAL_ALE solid mesh motion model (see Mesh Motion card). More than likely, these conditions are applied together with geometry conditions on the mesh equations, e.g. PLANE, DX, DY, GEOM, etc., on the same boundary. TOTAL_ALE mesh motion involves two sets of elasticity equations: mesh motion equations (mesh1 and mesh2), and real-solid elasticity equations (mom_solid1 and mom_solid2).

References¶

GT-005.3: THE NEW TOTAL-ARBITRARY-LAGRANGIAN-EULERIAN (TALE) CAPABILITY and its applicability to coating with/on deformable media, August 6, 1999, P. R. Schunk

FORCE_RS¶

BC = FORCE_RS SS <bc_id> <float1> <float2> <float3>

Description / Usage¶

(WIC/VECTOR REALSOLID)

This boundary condition card applies a force per unit area (traction) on a real-solid material region (as opposed to a Lagrangian solid region), as is the case with TOTAL_ALE mesh motion type (see Mesh Motion card). The force per unit area is applied uniformly over the boundary delineated by the side set ID. The applied force is of course a vector. Definitions of the input parameters are as follows:

FORCE_RS	Name of the boundary condition (<bc_name>)
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	X-component of traction in units of force/area.
<float2>	Y-component of traction in units of force/area.
<float3>	Z-component of traction in units of force/area.

Examples¶

Following is a sample card:

BC = FORCE_RS SS 10 0. 1.0 1.0

This card results in a vector traction defined by \(\vec F\) = 0.0(\(\vec ex\)) + 1.0(\(\vec ey\)) + 1.0(\(\vec ez\)) applied to the side set boundary delineated by flag 10, where the element block bounded by this boundary is of a TOTAL_ALE mesh motion type.

Technical Discussion¶

It is important to note that this boundary condition can only be applied to TOTAL_ALE mesh motion types (cf. Mesh Motion card). (see FORCE for all other mesh motion types). Furthermore, it is rare and unlikely that this boundary condition be applied to ARBITRARY mesh motion regions. As an example of how this boundary condition card is used, consider the need to apply some load pressure to a real solid of a TOTAL_ALE region, like a rubber roller, so as to squeeze and drive flow in a liquid region. Some of the usage tutorials cited below will direct you to some specifics.

FAQs¶

On internal two-sided side sets, this boundary condition results in double the force in the same direction.

References¶

GT-005.3: THE NEW TOTAL-ARBITRARY-LAGRANGIAN-EULERIAN (TALE) CAPABILITY and its applicability to coating with/on deformable media, August 6, 1999, P. R. Schunk

SAND2000-0807: TALE: An Arbitrary Lagrangian-Eulerian Approach to Fluid- Structure Interaction Problems, P. R. Schunk (May 2000)

NORM_FORCE_RS¶

BC = NORM_FORCE_RS SS <bc_id> <float1> <float2> <float3>

Description / Usage¶

(WIC/VECTOR REALSOLID)

This boundary condition card applies a force per unit area (traction) on a real-solid in a TOTAL_ALE mesh region (see Mesh Motion card). The force per unit area is applied uniformly over the boundary delineated by the side set ID. The applied traction is of course a vector. Unlike the FORCE_RS boundary condition card, the vector traction here is defined in normal-tangent vector basis. Definitions of the input parameters are as follows:

NORM_FORCE_RS	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	Normal component of traction in units of force/area.
<float2>	Tangential component of traction in units of force/area.
<float3>	Second tangential component of traction in units of force/area (in 3-D).

This card actually applies a traction that is then naturally integrated over the entire side set of elements. Hence, the units on the floating point input must be force/area.

Examples¶

The following is a sample input card:

BC = NORM_FORCE_RS SS 10 0. 1.0 1.0

This card results in a vector traction to the real-solid in a TOTAL_ALE mesh motion type (not the mesh) defined by \(\vec F\) = 0.0(\(\vec n\)) + 1.0(\(\vec t_1\)) + 1.0(\(\vec t_2\)) applied to the side set boundary delineated by flag 10. The normal vector is defined as the outward pointing normal to the surface. For internal surfaces defined by side sets which include both sides of the interface, this condition will result in exactly a zero traction, i.e., internal surface side sets must be attached to one element block only to get a net effect.

Technical Discussion¶

It is important to note that this boundary condition can only be applied to TOTAL_ALE mesh motion types (cf. Mesh Motion card). As an example of how this boundary condition card is used, consider the need to apply some load pressure uniformly on the inside of a solid-membrane (like a pressurized balloon). In more advanced usage, one could tie this force to an augmenting condition on the pressure, as dictated by the ideal gas law.

This boundary condition is not used as often as the FORCE_RS or FORCE_USER_RS counterparts.

References¶

No References.

REP_FORCE_RS¶

BC = REP_FORCE_RS SS <bc_id> <floatlist>

Description / Usage¶

(WIC/VECTOR REALSOLID)

This boundary condition card applies a force per unit area (traction) that varies as the inverse of the fourth power of the distance from a planar surface (see Technical Discussion below) on a TALE or Dynamic Lagrangian mesh region. This boundary condition can be used to impose a normal contact condition (repulsion) or attraction condition (negative force) between a planar surface and the surface of a TALE region. It differs from REP_FORCE card only in the mesh-motion type to which it applies. The force per unit area is applied uniformly over the boundary delineated by the side set ID. The applied force is a vector in the normal direction to the Lagrangian interface.

Definitions of the input parameters are as follows, where <floatlist> has five parameters:

REP_FORCE_RS	Name of the boundary condition (<bc_name>)
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	Coefficient of repulsion, \(\lambda\).
<float2>	Coefficient a of plane equation.
<float3>	Coefficient b of plane equation.
<float4>	Coefficient c of plane equation.
<float5>	Coefficient d of plane equation.

Examples¶

The following is a sample input card:

BC = REP_FORCE_RS SS 10 1.e+03. 1.0 0.0 0.0 -3.0

This card results in a vector traction in the normal direction on surface side set 10 defined by \(\vec F\) = –1.0e3 ⁄ \(h^4\) where F is a force per unit area that varies with the distance h from the plane specified by 1.0x – 3.0 = 0.0 .

Technical Discussion¶

The repulsive force is defined by \(\vec F\) = F(\(\vec n\)) where F is a force per unit area that varies with the distance h from a plane defined by the equation ax + by + cz + d = 0. The magnitude of the function \(\vec F\) is defined as:

The normal vector is defined as the outward pointing normal to the surface. For internal surfaces defined by side sets which include both sides of the interface, this condition will result in exactly a zero traction, i.e., internal surface side sets must be attached to one material only to get a net effect.

It is important to note that this boundary condition can only be applied to TALE mesh motion types (cf. Mesh Motion card). As an example of how this boundary condition card is used, consider the need to apply some load pressure uniformly on a surface that is large enough such that this surface never penetrates a predefined planar boundary. This condition hence can be use to impose an impenetrable contact condition.

References¶

GT-005.3: THE NEW TOTAL-ARBITRARY-LAGRANGIAN-EULERIAN (TALE) CAPABILITY and its applicability to coating with/on deformable media, August 6, 1999, P. R. Schunk

FORCE_USER_RS¶

BC = FORCE_USER_RS SS <bc_id> <float1>...<floatn>

Description / Usage¶

(WIC/VECTOR REALSOLID)

This boundary condition card applies a user-defined force per unit area (traction) on a TOTAL_ALE real solid region (see Mesh Motion card). It differs from its counterpart FORCE_USER only in the type of material to which the force is applied, as described on the Mesh Motion card. The functional form of the force is programmed in the function force_user_surf in bc_user.c, and can be made a function of any of the independent or dependent variables of the problem, including position (see example below). The force per unit area is applied to boundary delineated by the side set ID. Definitions of the input parameters are as follows:

FORCE_USER_RS	Name of the boundary condition (<bc_name>)
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>…<floatn>	Parameters list (length arbitrary) for parameterizing the user defined force. These parameters are accessed through the p[]array in force_user_surf.

Examples¶

The input card

BC = FORCE_USER_RS SS 3   {delta_t} 0.   1000.0 0.

used in conjuction with the following snippet of code in force_user_surf:

/* Comment this out FIRST!!!!! */
/* EH(-1,"No FORCE_USER model implemented"); */
/**************************** EXECUTION BEGINS
*******************************/
   if (time <= p[0])
      {
         func[0] = p[1]*time/p[0];
           func[1] = p[2]*time/p[0];
           func[2] = p[3]*time/p[0];
      }
  else
      {
           func[0] = p[1];
           func[1] = p[2];
           func[2] = p[3];
      }

applies a time-dependent force ramped from zero to 1000.0 in the +y direction over the time period {delta_t}. Note how p[0] is the time period, viz. {delta_t}, over which the force is ramped up.

Technical Discussion¶

Used commonly to apply a force per unit area to an external surface of a solid region (TOTAL_ALE type, cf. FORCE_USER), that is nonconstant, viz. time varying or spatially varying. The FORCE_RS and NORM_FORCE_RS boundary conditions can be used for constant forces. This condition is applied as a weak integrated condition in Goma, and hence will be additive with others of its kind.

References¶

No References.

SOLID_FLUID_RS¶

BC = SOLID_FLUID_RS SS <bc_id> <integer1> <integer2> [float]

Description / Usage¶

(PCC/VECTOR REALSOLID)

Used for fluid-structure interaction problems, the SOLID_FLUID_RS condition equates the normal traction between adjacent fluid and solid materials. (By “normal traction” we mean the tangential and normal force components, per unit area.) This condition is only to be used on boundaries between regions of ARBITRARY mesh motion with fluid-momentum equations and of TOTAL_ALE mesh motion (cf. SOLID_FLUID boundary condition card for LAGRANGIAN mesh motion regions), with solid momentum equations (or mesh equations) - see Mesh Motion and EQ cards. All elements on both sides of the interface must have the same element type (the same order of interpolation and basis functions) e.g., Q1 or Q2. Also, such interfaces must include element sides from both sides of the interface in the defining side set.

Definitions of the input parameters are as follows:

SOLID_FLUID_RS	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer1>	Element block ID of the solid phase (of TOTAL_ALE motion type) from the EXODUS II database.
<integer2>	Element block ID of the liquid phase from the EXODUS II database.
[float]	Scale factor for stress balance for nondimensionalization. This parameter, a multiplier on the liquid phase contribution, is optional; the default is 1.0.

Examples¶

The following set of input cards is a sample specification for a fluid-structure interaction problem:

BC = SOLID_FLUID_RS SS 5   2   1

BC = NO_SLIP_RS SS 5   2   1

BC = KIN_DISPLACEMENT SS   5   2

In this example, side set 5 is a boundary between a solid rubber blade and a liquid; the material in element block 2 is the blade, and the material in element block 1 is the fluid. Along the blade, a companion boundary condition is applied to ensure no slip on the same side set. Also, because this condition involves a TOTAL_ALE mesh region, a KIN_DISPLACEMENT boundary condition is needed on the same side set to force the solid boundary to follow the side set.

Technical Discussion¶

The functional form of the SOLID_FLUID_RS boundary condition is:

where \(\underline{T}\) is the fluid phase stress tensor given by any one of the specified fluid-phase constitutive equations, and \(\underline{\sigma}\) is the real-solid solid phase stress tensor, also given by any one of the solid-phase constitutive equation (see Mat file specifications). \(\lambda\) is a scaling factor that defaults to unity (and is usually best taken as such unless some scaling is invoked). With this boundary condition, the local residual and Jacobian contributions from the fluid mechanics momentum equations (on the ARBITRARY side of the boundary) are added into the weak form of the residual and Jacobian entries for the real-solid solid mechanics equations (viz. the EQ = mom_solid options on the real-solid TOTAL_ALE side of the boundary).

TOTAL_ALE mesh motion regions cannot be porous and deformable (as of 11/19/ 2001).

References¶

GT-005.3: THE NEW TOTAL-ARBITRARY-LAGRANGIAN-EULERIAN (TALE) CAPABILITY and its applicability to coating with/on deformable media, August 6, 1999, P. R. Schunk

SAND2000-0807: TALE: An Arbitrary Lagrangian-Eulerian Approach to Fluid- Structure Interaction Problems, P. R. Schunk (May 2000)

SPLINEXYZ_RS¶

Description / Usage¶

(PCC/MESH)

This card is used to specify a general surface (solid) boundary description for TOTAL_ALE real solid equations (see Mesh Motion card). These boundary conditions are tantamount to SPLINE_RS , except that they do not invoke a vector residual rotation into normal-tangential form. Instead, SPLINEX_RS invokes the geometric boundary condition on the x-component of the real solid equation residual, and so on. The card requires user-defined subroutines. Templates for these routines are currently located in the routine “user_bc.c”. Both a function routine, fnc, for function evaluation and corresponding routines dfncd1, dfncd2, and dfncd3 for the derivative of the function with respect to global coordinates are required. Note that it takes an arbitrary number of floating-point parameters, depending on the user’s needs.

Definitions of the input parameters are as follows:

{bc_name}	Boundary condition name that defines the general surface; the options are: SPLINEX_RS - X general surface SPLINEY_RS - Y general surface SPLINEZ_RS - Z general surface
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
[floatlist]	Constants to parameterize any f(x,y,z) = 0 function input in user-defined routine fnc.

Examples¶

The following is a sample input card:

BC = SPLINEZ_RS SS 10 1.0 100. 20.0 1001.0 32.0

applies a user-defined distinguishing condition parameterized by the list of floating points to the boundary defined by side set 10. Most importantly, the condition replaces the Z-component of the real solid equation.

Technical Discussion¶

The mathematical form of this distinguishing condition is arbitrary and is specified by the user in the fnc routine in user_bc.c. Derivatives of the user-specified function must also be provided so as to maintain strong convergence in the Newton iteration process. These functions are located next to fnc and are named dfncd1, dfncd2, and dfncd3.Several examples for simple surfaces exist in the template routine. In three dimensions, usage needs to be completed with a companion ROT input card which directs the equation application of the condition, even though rotations are not actually performed.

References¶

No References.

SPLINE_RS¶

BC = SPLINE_RS SS <bc_id> [floatlist]

Description / Usage¶

(PCC/VECTOR REALSOLID)

This card is used to specify a general surface (solid) boundary description for TOTAL_ALE type mesh motion (see Mesh Motion card). Like most other distinguishing conditions, this condition causes the real-solid equations, viz. solid1, solid2, and solid3, to be rotated into boundary normal-tangential form. The card requires user-defined subroutines. Templates for these routines are currently located in the routine “user_bc.c”. Both a function routine, fnc, for function evaluation and corresponding routines dfncd1, dfncd2, and dfncd3 for the derivative of the function with respect to global coordinates are required. . Note that it takes an arbitrary number of floating-point parameters, depending on the user’s needs.

Definitions of the input parameters are as follows:

SPLINE_RS	Name of the boundary condition <bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
[floatlist]	Constants to parameterize any f(x,y,z) = 0 function input in user-defined routine fnc.

Examples¶

The following is a sample input card:

BC = SPLINE_RS SS 10 1.0 100. 20.0 1001.0 32.0

applies a user-defined distinguishing condition, parameterized by the list of five floating point values, to the boundary defined by side set 10.

Technical Discussion¶

This condition is applied to the normal component of the real solid equations along a boundary in two dimensions; in three dimensions application needs to be further directed with the ROT conditions. Examples of typical distinguishing conditions can be found in user_bc.c in the fnc routine and companion derivative routines.

References¶

No References.

FRICTION_RS¶

BC = FRICTION_RS SS <bc_id> <float1> [integer1]>

Description / Usage¶

(WIC/VECTOR REAL SOLID)

This boundary condition card applies a force per unit area (traction) on the TOTAL_ALE solid mechanics equations. The force per unit area is applied according to Coulomb’s friction law over the boundary delineated by the side set ID. The applied traction is of course a vector. The vector traction is defined in normal-tangent vector basis. Definitions of the input parameters are as follows:

FRICTION_RS	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set.
<bc_id>	The boundary flag identifier, or a side set number which is an integer that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	\(\mu\), Coulombic coefficient of friction.
[integer1]	optional specification of the element block id to which this condition will be applied.

This card actually applies a traction that is then naturally integrated over the entire side set of elements.

Examples¶

Following is a sample card:

BC = FRICTION_RS SS 10 0.1 2

Technical Discussion¶

Important note: this boundary condition can only be applied to TOTAL_ALE mesh motion types (cf. Mesh Motion card). For other mesh motion types, refer to FRICTION.

This condition should be utilized in conjunction with a rotated condition such as SPLINE_RS in order to apply a tangential force which is proportional to the normal force;

where \(\mu\) is the coefficient of friction and \(\underline{v}\) is the velocity of the convected solid. Note that the direction of the frictional force is determined by the velocity direction.

Category 4: Fluid Momentum Equations¶

The fluid-momentum equations, e.g., the momentum equations in the Navier-Stokes system for incompressible flows, require many boundary conditions mainly because they are formulated in an arbitrary frame of reference. The plethora of boundary conditions here contain Dirichlet, finiteelement weak form, finite-element strong form, and many other boundary condition types.

UVW¶

BC = {U | V | W} NS <bc_id> <float1> [float2]

Description / Usage¶

(DC/MOMENTUM)

This Dirichlet boundary condition specification is used to set a constant velocity in the X-, Y-, or Z-direction. Each such specification is made on a separate input card. Definitions of the input parameters are as follows:

{U \| V \| W}	One-character boundary condition name (<bc_name>) that defines the velocity direction, where: U - Indicates X velocity component V - Indicates Y velocity component W - Indicates Z velocity component
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	Value of velocity component.
[float2]	An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

The following are sample input cards for the X velocity component Dirichlet card:

BC = U NS 7   1.50

BC = U NS 7   1.50   1.0

where the second example uses the “residual” method for applying the same Dirichlet condition.

Technical Discussion¶

This class of card is used to set Dirichlet conditions on the velocity components. When the second optional float parameter is not present, the matrix rows corresponding to the appropriate velocity component for nodes on this node set are filled with zeros, the diagonal element is set to one, the corresponding residual entry is also set to zero, and in the solution vector the appropriate degree of freedom is set to the value specified by <float1>. This is the so-called “hard set” method for specifying Dirichlet conditions.

An alternate method for specifying Dirichlet conditions is applied when the second float parameter is present (the actual value is not important except that it be different from -1.0). In this case, the Dirichlet constraint is applied as a residual equation. That is, the momentum equation for the appropriate component at each node in the nodeset is replaced by the residual equation,

This residual equation is included in the Newton’s method iteration scheme like any other residual equation. Note that in this case, nothing is set in the solution vector since that will occur automatically as part of the iteration method.

References¶

No References.

PUVW¶

BC = {PU | PV | PW}

Description / Usage¶

(DC/PMOMENTUM)

This card is currently not implemented.

Examples¶

No Examples.

Technical Discussion¶

No Discussion.

References¶

No References.

UVWVARY¶

BC = {UVARY | VVARY | WVARY} SS <bc_id> [float_list]

Description / Usage¶

(PCC/MOMENTUM)

The UVARY, VVARY and WVARY boundary condition format is used to set variation in X, Y, or Z velocity component, respectively, with respect to coordinates and time on a specified sideset. Each such specification is made on a separate input card.

The UVARY, VVARY, and WVARY cards each require user-defined functions be supplied in the file user_bc.c. Four separate C functions must be defined for a boundary condition: velo_vary_fnc, dvelo_vary_fnc_d1, dvelo_vary_fnc_d2, and dvelo_vary_fnc_d3. The first function returns the velocity component at a specified coordinate and time value, the second, third, and fourth functions return the derivative of the velocity component with x, y and z respectively.

A description of the syntax of this card follows:

{UVARY \| VVARY \| WVARY}	Five-character boundary condition name (<bc_name>) identifies the velocity component: UVARY -X velocity component VVARY -Y velocity component WVARY -Z velocity component
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
[float_list]	An optional list of float values separated by spaces which will be passed to the user-defined subroutines to allow the user to vary the parameters of the boundary condition. This list of float values is passed as a onedimensional double array designated p in the parameter list of all four C functions.

Examples¶

Following is a sample card for an X component

BC = UVARY SS 10 2.0 4.0

Following are the C functions that would have to be implemented in “user_bc.c” to apply the preceding boundary condition card to set a parabolic velocity profile along a sideset.

double velo_vary_fnc( const int velo_condition, const double x,
  const double y, const double z, const double p[], const double
  time )
{
double f = 0;
double height = p[0];
double max_speed = p[1];
  if ( velo_condition == UVARY ) {
  f = max_speed*( 1.0 - pow(y/height, 2 ) );
  }
return(f);
}
/* */
double dvelo_vary_fnc_d1( const int velo_condition, const double
  x, const double y, const double z, const double p[], const
  double time )
{
double f = 0;
return(f);
}
/* */
double dvelo_vary_fnc_d2( const int velo_condition, const double
  x, const double y, const double z, const double p[], const
  double time )
{
double f = 0;
double height = p[0];
double max_speed = p[1];
  if ( velo_condition == UVARY ) {
  f = -2.0*max_speed*(y/height)/height;
}
return(f);
}
/* */
double dvelo_vary_fnc_d3( const int velo_condition, const double
  x, const double y, const double z, const double p[], const
  double time )
{
double f = 0;
return(f);
}
/* */

Technical Discussion¶

Including the sensitivities is a pain, but required since Goma has no provision for computing Jacobian entries numerically.
Note that the type of boundary condition (UVARY, VVARY, or WVARY) is sent to each function in the velo_condition parameter. Since there can be only one set of definition functions in user_bc.c, this allows the user to overload these functions to allow for more than one component defined in this manner. It would also be possible to use these functions to make multiple definitions of the same velocity component on different sidesets. However, this would have to be done by sending an identifier through the p array.
This is a collocated-type boundary condition. It is applied exactly at nodal locations but has lower precedence of application than direct Dirichlet conditions.

References¶

No References.

UVWUSER¶

BC = {UUSER | VUSER | WUSER} SS <bc_id> <float_list>

Description / Usage¶

(SIC/MOMENTUM)

This card permits the user to specify an arbitrary integrated condition to replace a component of the fluid momentum equations on a bounding surface. Specification of the integrand is done via the functions uuser_surf, vuser_surf and wuser_surf in file “user_bc.c.”, respectively.

A description of the syntax of this card follows:

{UUSER \| VUSER \| WUSER}	Five-character boundary condition name (<bc_name>) identifies the momentum equation component: UUSER - X momentum component VUSER - Y momentum component WUSER - Z momentum component
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float_list>	A list of float values separated by spaces which will be passed to the user-defined subroutines so the user can vary the parameters of the boundary condition. This list of float values is passed as a one-dimensional double array to the appropriate C function.

Examples¶

The following is an example of card syntax:

BC = VUSER SS 10 1.0

Implementing the user-defined functions requires knowledge of basic data structures in Goma and their appropriate use. The uninitiated will not be able to do this without guidance.

References¶

No References.

NO_SLIP/NO_SLIP_RS¶

BC = {NO_SLIP | NO_SLIP_RS} SS <bc_id> <integer1> <integer2>

Description / Usage¶

(SIC/ VECTOR MOMENTUM)

This card invokes a special boundary condition that applies a no-slip condition to the fluid velocity at an interface between a liquid phase and a solid phase so that the fluid velocity and solid velocity will be in concert. The solid phase must be treated as a Lagrangian solid and may be in a convected frame of reference. The fluid velocity is equal to the velocity of the stress-free state mapped into the deformed state (for steadystate problems).

In general, a SOLID_FLUID boundary condition must also be applied to the same boundary so that the force balance between liquid and solid is enforced. Note that a FLUID_SOLID boundary condition will have no effect since the strongly enforced NO_SLIP/NO_SLIP_RS on the fluid momentum equation will clobber it.

All elements on both sides of the interface must have the same element type, i.e., the same order of interpolation and basis functions, e.g., Q1 or Q2.

Definitions of the input parameters are as follows:

{NO_SLIP \| NO_SLIP_RS}	Boundary condition name applied in the following formulations: NO_SLIP - this condition applies when the solid phase is a purely LAGRANGIAN solid. NO_SLIP_RS - this condition should be used instead when the displacements in the solid phase are determined via a TALE formulation.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain. This side set should be the intersection of liquid and solid element blocks and be defined so that it is present in both element blocks.
<integer1>	the element block ID number of the solid phase material.
<integer2>	the element block ID number of the liquid phase material.

Examples¶

The following is a sample input card:

BC= NO_SLIP SS 10   2 1

This card will enforce continuity of velocity between the solid phase in element block 2 with the fluid phase in element block 1. Side set 10 should be in common with both element blocks.

Technical Discussion¶

This boundary condition is a vector condition meaning that all three components of the fluid momentum equation are affected by use of a single boundary condition. The actual constraints that are imposed at node j are:

where \(\phi_j\) is the finite element trial function, \(v_f\) is the fluid velocity, and \(v_s\) is the solid phase velocity. These three constraints are strongly enforced so they replace completely the x, y, and z fluid momentum components. The boundary condition is not rotated since all three components of the momentum equation are supplanted.

As mentioned above this boundary condition is used most often in conjunction with the SOLID_FLUID boundary condition which equates stresses across fluid/ solid interfaces. As described in the section discussing this card, this latter card imposes these forces by using the residuals of the fluid momentum equation as surrogates for the fluid phase forces. These forces however are imposed on the solid equations prior to imposition of the NO_SLIP boundary condition.
As noted above, for this boundary condition to function properly it is necessary that the side set between the fluid and solid element block be present in both element blocks. To explain this it is necessary to recognize that side sets are defined as a set of faces attached to specific elements. This is in contrast to node sets which are simply a list of node numbers. Therefore, in the case of a side set that lies at the interface of two element blocks, it is possible for a given face in that side set to appear twice, once attached to the element in the first element block and a second time attached to the adjoining element in the second element block. This is the condition that is required for the proper execution of this boundary condition. Fortunately, this is the default of most meshing tools that interface with Goma.
It is also important to reiterate that another necessary condition for the proper function of this boundary condition is that the interpolation order of the pseudosolid mesh unknowns and the fluid velocity unknowns in the ALE fluid phase block be identical to the interpolation order of the solid displacement unknowns in the LAGRANGIAN or TALE adjoining solid phase block. This usually means that the element type must be the same in both phases. In two-dimensions this generally is not a problem, but in three dimensions it can impose a considerable hardship on the analyst.

References¶

No References.

VELO_NORMAL¶

BC = VELO_NORMAL SS <bc_id> <float> [integer]

Description / Usage¶

(SIC/ROTATED MOMENTUM)

This boundary condition allows the user to set the outward velocity component normal to a surface.

Definitions of the input parameters are as follows:

VELO_NORMAL	Boundary condition designation.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float>	\(V_n\), value of the normal velocity component. Note that this velocity component is relative to the motion of the underlying mesh.
[integer]	blk_id, an optional parameter that is the element block number in conjugate problems that identifies the material region where the VELO_NORMAL condition will be applied (usually the liquid element block in solid/liquid conjugate problems). For external boundaries, this optional parameter can be set to unity to force the condition to be kept at a corner between two side sets (2D only). This is handy for corner conditions. Please see GTM-004.0 for details.

Examples¶

The following is a sample input card:

BC = VELO_NORMAL SS 10   0.0

This boundary condition will enforce an impenetrability constraint over side set 10 as it excludes normal velocity of the fluid relative to the mesh. This is by far the most common context for this boundary condition.

Technical Discussion¶

The actual weighted residual equation that is applied to a node, j, on the surface in question is as follows:

where \(\phi_j\) is the finite element trial function, n the outward-pointing normal to the surface, v the fluid velocity, \(v_s\) the velocity of the underlying mesh, and \(v_n\) is the normal velocity set by \(V_n\) (the input value).

This constraint is a rotated strongly integrated equation so that it will replace one of the rotated components of the fluid momentum equation. This component should generally always be the normal rotated component. In two dimensions, this replacement is automatic. In three dimensions, this replacement must be specified by a ROT condition.
This card applies the identical constraint that is applied by the KINEMATIC boundary condition. The only difference is that this card replaces the normal component of the rotated fluid momentum equation, while the latter card replaces the normal component of the rotated (pseudo-solid) mesh momentum equation.
In conjugate liquid/solid problems, the VELO_NORMAL condition is often used to enforce the impenetrability condition of the liquid/solid interface. The optional blk_id parameter can be used to insure that the VELO_NORMAL condition is correctly applied to the liquid side of the interface. blk_id should be set equal to the element block ID of the liquid in this case. This also applies to the KINEMATIC and KINEMATIC_PETROV boundary conditions.

References¶

GT-001.4: GOMA and SEAMS tutorial for new users, February 18, 2002, P. R. Schunk and D. A. Labreche

GTM-004.1: Corners and Outflow Boundary Conditions in Goma, April 24, 2001, P. R. Schunk

VELO_NORMAL_LS¶

BC = VELO_NORMAL_LS SS <bc_id> 0.0 <blk_id> <float1> <float2>

Description / Usage¶

(SIC/ROTATED MOMENTUM)

This boundary condition relaxes the VELO_NORMAL condition in the light phase of a level-set simulation, thereby allowing gas to escape from a confined space.

Definitions of the input parameters are as follows:

VELO_NORMAL_LS	Boundary condition designation.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<blk_id>	blk_id, an optional parameter that is the element block number in conjugate problems that identifies the material region where the VELO_NORMAL_LS condition will be applied (usually the liquid element block in solid/liquid conjugate problems). For external boundaries, this optional parameter can be set to unity to force the condition to be kept at a corner between two side sets (2D only). This is handy for corner conditions. Please see GTM-004.0 for details.1
<float>	L=interface half-width over which the VELO_NORMAL bc changes.
<float2>	alpha=shift in the VELO_NORMAL change relative to the LS interface. With alpha=0, VELO_NORMAL begins to be enforced when the LS interface reaches a distance L from a wall. With alpha=1, VELO_NORMAL begins to be enforced when the LS inteface reaches the wall.

Examples¶

The following is a sample input card:

BC = VELO_NORMAL_LS SS 10   0.0 {blk_id=1} 0.05 0.4.

Technical Discussion¶

The technical discussion under VELO_NORMAL largely applies here as well.

References¶

GT-001.4: GOMA and SEAMS tutorial for new users, February 18, 2002, P. R. Schunk and D. A. Labreche

GTM-004.1: Corners and Outflow Boundary Conditions in Goma, April 24, 2001, P. R. Schunk

VELO_NORM_COLLOC¶

BC = VELO_NORM_COLLOC SS <bc_id> <float>

Description / Usage¶

(PCC/ROTATED MOMENTUM)

This boundary condition allows the user to set the outward velocity component normal to a surface. It is identical in function to the VELO_NORMAL boundary condition, but differs in that it is applied as a point collocated condition.

Definitions of the input parameters are as follows:

VELO_NORM_COLLOC	Boundary condition designation.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float>	\(V_n\), value of normal velocity component. Note that this velocity component is relative to the motion of the underlying mesh.

Examples¶

Following is a sample card:

BC = VELO_NORM_COLLOC SS 20 0.0

This boundary condition will enforce an impenetrability constraint over side set 20 as it excludes normal velocity of the fluid relative to the mesh. This is by far the most common context for this boundary condition.

Technical Discussion¶

The actual equation that is applied to a node, j, on the surface in question is as follows:

where \(v_j\) is the fluid velocity at the node, n the outward-pointing normal to the surface, \(v_s\) the velocity of the underlying mesh at the node, and \(v_n\) is the normal velocity set by <float> above.

This constraint is a rotated collocated equation so that it will replace one of the rotated components of the fluid momentum equation. This component should generally always be the normal rotated component. In two dimensions, this replacement is automatic. In three dimensions, this replacement must be specified by a ROT condition.
As noted above this boundary condition applies exactly the same constraint as the VELO_NORMAL condition but via a point collocated method instead of as a strongly integrated condition. This might be advantageous at times when it is desirable to enforce a normal velocity component unambiguously at a point in the mesh.

VELO_NORMAL_DISC¶

BC = VELO_NORMAL_DISC SS <bc_id> <float>

Description / Usage¶

(SIC/ROTATED MOMENTUM)

This boundary condition card balances mass loss from one phase to the gain from an adjacent phase. It is the same as the KINEMATIC_DISC card but is applied to the fluid momentum equation. The condition only applies to interphase mass, heat, and momentum transfer problems with discontinuous (or multivalued) variables at an interface, and it must be invoked on fields that employ the Q1_D or Q2_D interpolation functions to “tie” together or constrain the extra degrees of freedom at the interface in question.

Definitions of the input parameters are as follows:

VELO_NORMAL_DISC	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain. It is important to note that this side set should be shared by both element blocks for internal boundaries.
<float>	Set to zero for internal interfaces; otherwise used to specify the mass average velocity across the interface for external boundaries.

Examples¶

Following is a sample card:

BC = VELO_NORMAL_DISC SS 66 0.0

is used at internal side set 10 (note, it is important that this side set include elements from both abutting materials) to enforce the overall conservation of mass exchange.

Technical Discussion¶

This boundary condition card applies the following constraint to nodes on the side set:

where 1 denotes evaluation in phase 1 and 2 denotes evaluation in phase 2. This constraint replaces only one of the momentum equations present at an internal discontinuous boundary between materials. There usually must be another momentum boundary condition applied to this side set. In addition, there must also be a distinguishing condition applied to the mesh equations if mesh motion is part of the problem.

This boundary condition is typically applied to multicomponent two-phase flows that have rapid mass exchange between phases, rapid enough to induce a diffusion velocity at the interface, and to thermal contact resistance type problems. The best example of this is rapid evaporation of a liquid component into a gas.

References¶

No References.

VELO_NORMAL_EDGE¶

BC = VELO_NORMAL_EDGE SS <bc_id1> <bc_id2> <float>

Description / Usage¶

(PCC-EDGE/ROTATED MOMENTUM)

This boundary condition card is used to specify the normal velocity component on a dynamic contact line in three-dimensions. The velocity component is normal to the contact line in the plane of the web and is equal to \(V_n\). The free-surface side set should always be <bc_id1>, the primary side set, and the web side set should be <bc_id2>, the secondary side set. Usually, this boundary condition is used to model dynamic contact lines in three dimensions and is usually found in conjunction with a VELO_TANGENT_EDGE card, a VAR_CA_EDGE or CA_EDGE card as explained below.

Definitions of the input parameters are as follows:

VELO_NORMAL_EDGE	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id1>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain. This is the primary side set defining the edge and should also be associated with the capillary free surface if used in the context of a dynamic contact line.
<bc_id2>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain. Together with <bc_id1>, this secondary side set defines the edge/curve on which the boundary condition applies as the intersection of the two side sets. In problems involving dynamic contact lines, this side set should correspond to the moving substrate.
<float>	\(V_n\), a parameter supplying the imposed normal velocity component. This component is taken normal to the edge curve parallel to <bc_id2>. See below for a more detailed description.

Examples¶

The following is a sample input card:

BC = VELO_NORMAL_EDGE SS 5 4 0.0

This card sets the normal-to-contact line component of the velocity to zero along the curve defined by the intersections of side set 5 and 4.

Technical Discussion¶

This boundary condition imposes a point collocated constraint of the form:

where v is the fluid velocity, \(v_m\) is the mesh velocity and \(n_cl\) is the normal to the contact line in the plane of <bc_id2>. The sketch at right depicts the orientation of this latter vector. Note that the collocation points for this boundary condition only are not the nodes on the edge curve but integration points in each of the edge elements. The reason for this is historical and uninteresting from a user point of view.

This boundary condition is used almost exclusive in problems involving dynamic contact lines in three dimensions. Imposition of wetting line physics is a difficult problem in modeling situations involving dynamic contact lines. In twodimensions, the assumption is often made that the effect of any wetting line force is to locally produce a condition in which the fluid velocity at the contact line is zero in the laboratory reference frame. That is to say, that at the contact line noslip between fluid and moving substrate is not enforced and instead a zero velocity condition is imposed. In this way, the difficult-to-model wetting line forces are not included directly, but instead are included by their effect on the velocity. One might argue with this model, and many do, but as a practical approach, this has been shown to work well.

Generalizing this notion into three dimensions is the primary motivation for this boundary condition. In the case of a dynamic contact line that is a curve in three dimensions, it is not correct to simply set all velocity components to zero because that would imply that the wetting forces act equally in all three directions. It is more reasonable to say that the wetting forces can act only in a direction normal to the contact line in the plane of the substrate. Therefore, the correct generalization of the wetting line model described in the previous paragraph is to set the velocity component normal to the contact line in the plane of the substrate to zero. This is done by using the VELO_NORMAL_EDGE boundary condition with \(V_n\) set to zero. In the case of a transient problem, it is necessary to add the qualifier, “relative to the mesh motion.” This accounts for the mesh motion velocity in the constraint equation. See Baer, et.al. (2000) for a more complete discussion of this wetting line model.
Generally, a VELO_NORMAL_EDGE card must be accompanied by other boundary conditions for a correct application. Firstly, since VELO_NORMAL_EDGE forces the velocity vector to be parallel to the contact line (at least in steady state), the KINEMATIC condition on any free surface attached to the contact line will overspecify the problem at the contact line. For this reason, it is generally the case that a CA_EDGE, VAR_CA_EDGE or VAR_CA_USER (or their variants) should also be present for the contact line. These boundary conditions replace the KINEMATIC card on the mesh at the contact line.

In addition, a VELO_TANGENT_EDGE card should be present to enforce no-slip between fluid and substrate in the tangential direction. Also it should be recognized that VELO_NORMAL_EDGE will not override other Dirichlet conditions on the substrate side set. Typically, the latter are used to apply no slip between fluid and substrate. If such conditions are used over the entirety of the substrate side set, both VELO_NORMAL_EDGE and VELO_TANGENT_EDGE conditions applied at the contact will be discarded.

There are two potential solutions to this. First, the substrate region could be divided into two side sets, a narrow band of elements adjacent to the contact line and the remainder of substrate region. In the narrow band of elements, the no slip condition is replaced by a VELO_SLIP card with the substrate velocity as parameters. This allows the velocity field to relax over a finite region from the velocity imposed at the contact line to the substrate field. The second method uses only a single side set for the substrate region, but replaces the Dirichlet no slip boundary conditions with a penalized VELO_SLIP condition. That is, the slip parameter is set to a small value so that no slip is effectively enforced, but within the context of a weakly integrated condition. Since the VELO_NORMAL_EDGE and VELO_TANGENT_EDGE cards are strongly enforced on the contact lines, the VELO_SLIP card will be overridden in those locations and the velocity field will deviate appropriately from the substrate velocity.

References¶

Baer, T.A., R.A. Cairncross, P.R.Schunk, R.R. Rao, and P.A. Sackinger, “A finite element method for free surface flows of incompressible fluids in three dimensions. Part II. Dynamic wetting lines.” IJNMF, 33, 405-427, (2000).

VELO_NORMAL_EDGE_INT¶

BC = VELO_NORMAL_EDGE_INT SS <bc_id1> <bc_id2> <float>

Description / Usage¶

(SIC-EDGE/ROTATED MOMENTUM)

This boundary condition card is used to specify the normal velocity component on a dynamic contact line in three-dimensions. The velocity component is normal to the contact line in the plane of the web and is equal to \(V_n\). The free-surface side set should always be <bc_id1>, the primary side set, and the web side set should be <bc_id2>, the secondary side set. This boundary condition is identical in function to VELO_NORMAL_EDGE. It differs only in that is applied as a strongly integrated condition along the curve defined by <bc_id1> and <bc_id2>.

Definitions of the input parameters are as follows:

VELO_NORMAL_EDGE_INT	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id1>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) for the primary side set in the problem domain. This side set should also be the side set associated with the capillary free surface if used in the context of a dynamic contact line.
<bc_id2>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) for the secondary side set defining the edge in the problem domain. Together with <bc_id1>, this defines the curve on which the boundary condition applies as the intersection of the two side sets. In problems involving dynamic contact lines, this side set should correspond to the moving substrate.
<float>	\(V_n\), a parameter supplying the imposed normal velocity component value. This component is taken normal to the edge curve parallel to <bc_id2>. See below for a more detailed description.

Examples¶

The following is a sample card:

BC = VELO_NORMAL_EDGE_INT SS 5 4   0.0

This card sets the normal-to-contact line component of the velocity to zero along the curve defined by the intersections of side set 5 and 4.

Technical Discussion¶

This boundary condition imposes a strongly integrated constraint of the form:

where \(\phi_i\) is the velocity trial function, v is the fluid velocity, \(v_m\) is the mesh velocity and \(n_cl\) is the normal to the contact line in the plane of the moving substrate <bc_id2>. The sketch at right depicts the orientation of this latter vector.

As noted above, this boundary condition functions nearly identically to the VELO_NORMAL_EDGE condition (except for its manner of application within Goma) and all comments appearing for the latter apply equally well for this boundary condition.

References¶

No References.

VELO_TANGENT¶

BC = VELO_TANGENT SS <bc_id> <integer> <float_list>

Description / Usage¶

(SIC/ROTATED MOMENTUM)

This boundary condition is used to specify strongly the component of velocity tangential to the side set. An added feature is the ability to relax the condition near a point node set according to supplied length scale and slipping parameters. This has application to problems involving moving contact lines. Note that this boundary condition is applicable only to two-dimensional problems and will result in an error if it is used in a three-dimensional context.

The <float_list> has three parameters; definitions for all input parameters is as follows:

VELO_TANGENT	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer>	\(N_cl\), parameter that identifies a single-node node set that coincides with the location in the model of the moving contact line. Distances in the slipping model are computed relative to the location of this node. When the slipping model is not used, this parameter can safely be set to zero. Another toggle setting can be triggered by setting this integer to -1; with this the VELO_TANGENT condition is kept at a rolling motion dynamic contact line. (See FAQ below on rolling motion conditions.)
<float1>	\(v_t\), a parameter specifying the value of the tangent velocity component. The component direction is n × k where k is the z-component unit vector.
<float2>	\(\beta\), a parameter specifying the coefficient for slip velocity (see model below); setting \(\beta\) to zero disables the slipping model.
<float3>	\(\alpha\), a parameter specifying the length scale for the position dependent slip (see model below); setting \(\alpha\) to zero disables the slipping model.

Examples¶

The following is a sample input card:

BC = VELO_TANGENT SS 10 100 0.0 1.0 0.1

Technical Discussion¶

Most often this boundary condition is used only to set the tangential speed on a side set because simpler Dirichlet conditions are not appropriate. An example is a sloping fully-developed inlet plane which does coincide with a coordinate axis. In this case, this boundary condition would be used to set the tangential velocity to be zero. The constraint applied at node i is as follows:

Alternatively, a dynamic contact line might be present in the problem and it is desirable that this condition be relaxed near the position of this contact line. This can be done by supplying non-zero values for \(\alpha\) and \(\beta\). In this case, the constraint that is applied at the \(i^{th}\) node on the boundary is:

in which d is the straightline distance to the node attached to <\(N_{cl}\)> and \(\dot{x}\) is the velocity vector of the mesh. It should be recognized that for steady state problems the mesh motion is by definition always zero so this constraint reverts to the previous expression.

FAQs¶

Rolling Motion Conditions for high Capillary number dynamic wetting. Often times it is desirable to model a case of dynamic wetting for which the conditions result in a high capillary number. At this limit, it is well known that a contact angle specification is in fact an overspecification. Goma has always been able to model this case, except recently some changes have been made to allow for the combination of conditions at a dynamic contact line to be controlled. It should be stressed that all finite capillary number cases still work as always. This FAQ addresses the special case in which you desire to specify no-slip right up to the contact line. In most cases a VELO_SLIP card or outright setting the velocity components to zero at the moving contact line in order to impart slip will circumvent the issue taken up here.

The figure below diagrams the situation:

Basically the web in this example corresponds to side set 5 and the free surface to side set 4. The conditions we desire in the vicinity of the contact line are as follows:

    $web surface
BC = VELO_TANGENT SS 5   0   {web_sp}   0.0   0.0
BC = VELO_NORMAL SS 5   0.0
BC = GD_PARAB   SS 5   R_MESH2   0   MESH_POSITION1   0   0. 0. 1.
BC = GD_PARAB   SS 5   R_MESH2   0 MESH_POSITION2   0 0.   {2*roll_rad} 1.
$   upstream heel
BC = KINEMATIC SS 4 0.
BC = CAPILLARY   SS   4 {inv_cap}   0.0   0.0

Notice how there is no contact angle specified and even with the CAPILLARY card, the effect of,

VELO_NORMAL, surface tension is very small. The desired set of conditions that should be applied at the dynamic contact line are as follows:

    At node 1:
R_MOMENTUM1   gets VELO_NORMAL   from SS 5, CAPILLARY   from SS 4,
R_MOMENTUM2   gets VELO_TANGENT   from SS 5, CAPILLARY   from SS 4,
R_MESH1   gets KINEMATIC   from SS 4,
R_MESH2   gets GD_PARAB   from SS 5, GD_PARAB   from SS 5,

This clearly shows that at the contact line, which happens to be node number 1 as shown by this clip from the BCdup.txt file resulting from the run, both VELO_NORMAL and VELO_TANGENT cards are applied, which implies no-slip. This is the so-called rolling-motion case (or tank-tread on a moving surface) in which the “kinematic paradox” is no longer a paradox. That is, both the KINEMATIC condition on the free surface and the no-slip condition on the substrate can be satisfied without loss or gain of mass through the free surface (see Kistler and Scriven, 1983). In order to make sure that both the combination above is applied, a “-1” must be placed in the first integer input of the VELO_TANGENT card, vis.,

BC = VELO_TANGENT SS 5   -1 {web_sp}   0.0   0.0

This integer input slot is actually reserved for a variable slip coefficient model and is normally used to designate the nodal bc ID of the contact line. In this case of no-slip, it is not needed so we added this special control. If the following card is issued:

BC = VELO_TANGENT SS 5   0 {web_sp}   0.0   0.0

then the following combination results:

    At node 1:
R_MOMENTUM1 gets   VELO_NORMAL   from SS 5, CAPILLARY   from SS 4,
R_MOMENTUM2 gets   CAPILLARY   from SS 4,
R_MESH1 gets   KINEMATIC   from SS 4,
R_MESH2 gets   GD_PARAB   from SS 5, GD_PARAB   from SS 5,

which is desired in the case for which a contact angle and liquid slip is applied.

References¶

Kistler, S. F. and Scriven, L. E. 1983. Coating Flows. In Computational Analysis of Polymer Processing. Eds. J. A. Pearson and S. M. Richardson, Applied Science Publishers, London.

VELO_TANGENT_EDGE¶

BC = VELO_TANGENT_EDGE SS <bc_id1> <bc_id2> <float_list>

Description / Usage¶

(PCC-EDGE/ROTATED MOMENTUM)

This boundary condition card is used to make the velocity component tangent to the contact line in the plane of the web equal to the component of web velocity (\(W_x\), \(W_y\), \(W_z\)) along the contact line. This constraint replaces the tangential component of the MOMENTUM equation along the contact line. It is used with the VELO_NORMAL_EDGE condition to impose a wetting line model onto dynamic contact lines in three-dimensions. The constraint is a rotated collocated condition.

Definitions of the input parameters are as follows:

VELO_TANGENT_EDGE	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id1>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) of the primary side set defining the edge geometry in the problem domain. When applied to dynamic contact lines, this side set should correspond to the free surface.
<bc_id2>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) of the secondary side set defining the edge geometry in the problem domain. The boundary condition is applied to the curve defined as the intersection of this side set with the primary side set When applied to dynamic contact lines, this side set should correspond to the substrate.
<float1>	\(W_x\), x-component of the substrate (or web) velocity.
<float2>	\(W_y\), y-component of the substrate (or web) velocity.
<float3>	\(W_z\), z-component of the substrate (or web) velocity.

Examples¶

The following is a sample input card:

BC = VELO_TANGENT_EDGE SS 5 4 -1.0 0.0 0.0

This card imposes a tangent velocity component along the curve formed by the intersection of sidesets 5 and 4. The value of the component is the projection of the substrate velocity (-1.0, 0. ,0.) into the tangent direction. The tangent direction is along the curve itself.

Technical Discussion¶

This equation imposes the following constraint as a point collocated condition at the integration points of the elements along the curve:

where \(t_{cl}\) is a vector tangent to the curve, v is the fluid velocity, and W is the (constant) velocity of the moving substrate. The reader is referred to the sketch appearing with the VELO_NORMAL_EDGE card for a depiction of these vectors. It is applied as a point collocated condition at the integration points of the line elements along the curve.

As noted above this boundary condition is used in concert with the VELO_NORMAL_EDGE condition to impose a model of wetting line physics along a dynamic contact line in three dimensions. The reader is referred to the discussion section of this latter boundary condition for a thorough exposition of this model. Suffice it to say that this boundary condition enforces no-slip between substrate and fluid in the tangent direction to the contact line. This is an essential part of the wetting line model because it implies that the wetting line forces related to surface tension etc. do not act tangential to the wetting line. Therefore, there is no agent in this direction which could account for departures from a strictly no-slip boundary condition.
The astute user might note that the mesh velocity doesn’t appear in this expression whereas it does in the expression for VELO_NORMAL_EDGE. In the latter expression, the normal motion of the mesh represents the wetting velocity of the contact line normal to itself. It has a physical significance and so it make senses to connect it to the fluid velocity at that point. In the case of the tangential mesh motion velocity, it cannot be attached to any obvious physical part of the wetting model. It makes no sense that the tangential motion of nodes along the contact line should induce velocity in the fluid and vice versa. As a result, mesh motion is left out of the preceding relation.

VELO_TANGENT_EDGE_INT¶

BC = VELO_TANGENT_EDGE_INT SS <bc_id1> <bc_id2> <float_list>

Description / Usage¶

(SIC-EDGE/ROTATED MOMENTUM)

This boundary condition card is used to make the velocity component tangent to the contact line in the plane of the web equal to the component of web velocity (\(W_x\), \(W_y\), \(W_z\)) along the contact line. It imposes the identical constraint as the VELO_TANGENT_EDGE card, but applies it as a strongly integrated condition rather than a point collocated condition.

Definitions of the input parameters are as follows:

VELO_TANGENT_EDGE_INT	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id1>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) of the primary side set defining the edge geometry in the problem domain. When applied to dynamic contact lines, this side set should correspond to the free surface.
<bc_id2>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) of the secondary side set defining the edge geometry in the problem domain. The boundary condition is applied to the curve defined as the intersection of this side set with the primary side set When applied to dynamic contact lines, this side set should correspond to the substrate.
<float1>	\(W_x\), x-component of the substrate (or web) velocity.
<float2>	\(W_y\), y-component of the substrate (or web) velocity.
<float3>	\(W_z\), z-component of the substrate (or web) velocity.

Examples¶

The following is a sample input card:

BC = VELO_TANGENT_EDGE_INT SS 5 4   -1.0 0.0 0.0

This card imposes a tangent velocity component along the curve formed by the intersection of sidesets 5 and 4. The value of the component is the projection of the substrate velocity (-1.0, 0. ,0.) into the tangent direction. The tangent direction is along the curve itself.

Technical Discussion¶

This equation imposes the following constraint as a point collocated condition at the integration points of the elements along the curve:

where \(t_{cl}\) is a vector tangent to the curve, v is the fluid velocity, W is the (constant) velocity of the moving substrate, \(\phi_i\) is the shape function each node along the curve C. This integral condition is imposed strongly at each node. The reader is referred to the sketch appearing with the VELO_NORMAL_EDGE card for a depiction of these vectors.

The reader is referred to the VELO_TANGENT_EDGE discussion for information about the context in which this condition is applied. Because it is applied in a different fashion than the former condition, it sometimes is the case that it will allow more flexibility in situations involving many boundary conditions applied in close proximity. There may also be situations where an integrated constraint results in better matrix conditioning that a collocated constraint.

VELO_TANGENT_3D¶

BC = VELO_TANGENT_3D SS <bc_id> <float_list>

Description / Usage¶

(SIC/ROTATED MOMENTUM)

This boundary condition is the three dimensional analog of the VELO_TANGENT condition. It is used to strongly set the tangential velocity component along a side set in a three-dimensional problem. It is not a completely general condition since it can set only a single tangential velocity component. It can only be applied to flat surfaces or surfaces which have only one radius of curvature such as a cylinder.

The <float_list> requires four values be specified; a description of the input parameters follows:

VELO_TANGENT_3D	The name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	\(v_t\), the value assigned to the tangential velocity component.
<float2>	\(t_x\), the x-component of a unit normal vector tangent to the surface; this vector must be tangent at all points on the surface. The direction of the imposed tangential velocity component is n × t with n the outward-pointing normal.
<float3>	\(t_y\), the y-component of a unit normal vector tangent to the surface; this vector must be tangent at all points on the surface. The direction of the imposed tangential velocity component is n × t with n the outwardpointing normal.
<float4>	\(t_z\), the z-component of a unit normal vector tangent to the surface; this vector must be tangent at all points on the surface. The direction of the imposed tangential velocity component is n × t with n the outwardpointing normal.

Examples¶

The following is an example of the card:

BC = VELO_TANGENT_3D SS 10   1.0   0.0 0.0 1.0

One could use this card to set the tangential velocity on a cylindrically shaped side set 10 provided that the cylinders axis was parallel to the z-axis. In this fashion, the tangential velocity component perpendicular to the z-axis is set to 1.0.

Technical Discussion¶

The constraint applied to the velocity vector by this condition on the side set is:

where \(\tilde{t}\) = n × t with the components of t supplied on the card. The advantages of introducing the normal vector is that it permits use of this card on curving surfaces provided the curvature occurs in only one direction and a single tangent vector exists that is perpendicular to both the surface normal and the direction of curvature. This of course implies that the tangential component can only be applied in the direction of the curvature.

Such conditions are of course met by a planar surface, but also a cylindrical surface. In the latter case, the vector t should be parallel to the axis of the cylinder. One application for this condition is in three-dimensional eccentric roll coating in which the roll speed can be set using this condition. The axis vectors of both roll coaters are supplied on the card.

VELO_SLIP¶

BC = VELO_SLIP SS <bc_id> <float_list> [integer1] [float5]

Description / Usage¶

(WIC/VECTOR MOMENTUM)

This boundary condition allows for slip between the fluid and a boundary using an implementation of the Navier slip relation. This relation fixes the amount of slip as a function of the applied shear stress. The scaling between stress and slip is a user parameter. This implementation also permits (in two dimensions only) variable scaling dependent upon distance from a mesh node. The latter can be used in modeling dynamic contact lines. This condition cannot currently be used on connecting surfaces.

There are four required values in <float_list> and two optional values; definitions of the input parameters are as follows:

VELO_SLIP	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	\(\beta\), the slip coefficient. The inverse of \(\beta\) defines the scaling between stress and slip. Hence, for small values of \(\beta\), large shear stresses are needed for a given amount of slip, and conversely, for large values of \(\beta\), the amount of stress needed for the same degree of slip decreases (see below for a more rigorous description).
<float2>	\(v_{s,x}\), the x-component of surface velocity vector. This would be the x-component of the fluid velocity if a no slip condition were applied.
<float3>	\(v_{s,y}\), the y-component of surface velocity vector. This would be the y-component of the fluid velocity if a no slip condition were applied.
<float4>	\(v_{s,z}\), the z-component of surface velocity vector. This would be the z-component of the fluid velocity if a no slip condition were applied.
[integer]	\(N_{cl}\), a single-node node set identification number. When the variable coefficient slip relation is used, distance is measured relative to this node (see discussion below). Normally, this node set represents the location of the dynamic contact line. Note that this option is generally only used in two-dimensional simulations.
[float5]	\(\alpha\), the distance scale in the variable slip model (see the discussion below). Both \(N_{cl}\) and \(\alpha\) should be present to activate the variable slip model.

Examples¶

Following is a sample card without the optional parameters:

BC = VELO_SLIP SS 10 0.1 0.0 0.0 0.0

Technical Discussion¶

The general form of this boundary condition is

where \(\tau\) is the deviatoric portion of the fluid stress tensor, \(\beta\) is the Navier slip coefficient and \(v_s\) is the velocity of the solid surface. The velocity of the surface must be specified, as described in the Description/Usage subsection above. It is a weakly integrated vector condition, as noted above, so it will be added to each of the three momentum equation components.

This last point is important to keep in mind, especially when applying this condition to boundaries that are not parallel to any of the principle axes. It is possible under these circumstances that this condition will allow motion through a boundary curve in addition to slip tangential to it. This can be avoided by including a rotated boundary condition like VELO_NORMAL on the same sideset. This will cause the momentum equations to be rotated to normal and tangential components and also enforce no normal flow of the material. Whatever slipping that takes place will be in the tangential direction.

The variable slip coefficient model is quite simple: EQUATION, where d is the absolute distance from node \(N_{cl}\) identified on the card; the coefficients \(\beta\) and \(\alpha\) are also supplied on input. This relation is protected against overflowing as d increases. This model can be used to allow slipping to occur in a region close to the node set, but at points further removed, a no slip boundary (\(\beta\) large) is reinstated on the sideset.

VELO_SLIP_ROT¶

BC = VELO_SLIP_ROT SS <bc_id> <float_list> [integer] [float5]

Description / Usage¶

(WIC/VECTOR MOMENTUM)

This boundary condition is a variant of the VELO_SLIP boundary condition and serves much the same function: to allow the fluid to slip relative to a solid substrate boundary. The difference is that the assumed substrate is a rotating cylindrical surface with axis parallel to the z-direction. Also as in the VELO_SLIP case, an optional variable slip coefficient model is available that allows for slip to occur only in a region near to a mesh node. This boundary condition is applicable generally only to two-dimensional problems or very specialized three dimensional problems.

The <float_list> has four values and there are two optional values; definitions of the input parameters are as follows:

VELO_SLIP_ROT	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	\(\beta\) the slip coefficient. The inverse of \(\beta\) defines the scaling between stress and slip. Hence, for small values of \(\beta\), large shear stresses are needed for a given amount of slip, and conversely, for large values of \(\beta\), the amount of stress needed for the same degree of slip decreases (see below for a more rigorous description).
<float2>	\(\omega\), rotation rate of the cylindrical substrate surface in radians/T. Positive values for this parameter correspond to rotation in the clockwise direction.
<float3>	\(x_c\), the x-position of rotation axis.
<float4>	\(y_c\), the y-position of rotation axis.
[integer]	\(N_{cl}\), a single-node node set identification number. When variable coefficient slip relation is used, distance is measured relative to this node (see discussion below). For problems involving dynamic contact lines, this nodeset coincides with the location of the contact line.
[float5]	\(\alpha\), the distance scale in the variable slip model (see the discussion below). Both \(N_{cl}\) and \(\alpha\) should be present to activate the variable slip model.

Examples¶

The following is a sample card without the optional parameters:

BC = VELO_SLIP_ROT SS 10 0.1 3.14 0.0 1.0

This condition specifies a moderate amount of slip (0.1) on a cylindrical surface rotating at 3.14 rad/sec around the point (0.0,1.0).

Technical Discussion¶

The comments that appear in the Technical Discussion section of the VELO_SLIP card apply equally well here. In particular, the discussion of the variable slip coefficient model applies here as well. The only significant difference is that the velocity of the substrate is not a fixed vector; instead, it is tangent to the cylindrical substrate with a magnitude consistent with the radius of the cylinder and the rotation rate.

References¶

No References.

VELO_SLIP_FILL¶

BC = VELO_SLIP_FILL SS <bc_id> <float_list>

Description / Usage¶

(WIC/VECTOR MOMENTUM)

This boundary condition is applied only in problems involving embedded interface tracking, that is, level set or volume of fluid. As in the case of the VELO_SLIP card, it allows for slip to occur between fluid and solid substrate, but in this case slipping is allowed only in a narrow region around the location of the interface where it intercepts the solid boundary. Elsewhere, this boundary condition enforces a no-slip condition between fluid and substrate.

When using the level set tracking, slip is allowed only near the intersection of the zero level set contour and the substrate boundary, and then only in a region twice the level set length scale wide centered on the zero level set. When using volume of fluid, the criterion for slipping is that the absolute value of the color function should be less than 0.25.

This boundary condition is most often used in conjunction with the FILL_CA boundary condition. The latter applies forces to contact lines in order to simulate wetting line motion. These forces are applied in a weak sense to the same regions near the interface so it is necessary to use VELO_SLIP_FILL with a large slipping coefficient so that effectively no-slip is relaxed completely near the interface.

Definitions of the input parameters are as follows:

VELO_SLIP_FILL	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	\(\beta\), the slip coefficient. The inverse of \(\beta\) defines the scaling between stress and slip. The parameter supplied on the input deck is used only in the region define above. Elsewhere, the slip coefficient is uniformly set to \(10^{-6}\).
<float2>	\(v_{s,x}\), the x-component of surface velocity vector. This would be the x-component of the fluid velocity if a noslip condition were applied.
<float3>	\(v{s,y}\), the y-component of surface velocity vector. This would be the y-component of the fluid velocity if a noslip condition were applied.
<float4>	\(v{s,z}\), the z-component of surface velocity vector. This would be the z-component of the fluid velocity if a noslip condition were applied.

Examples¶

Following is a sample card without the optional parameters:

BC = VELO_SLIP SS 10 100000.0 0.0 0.0 0.0

The large value of slip coefficient ensures nearly perfect slip in the region around the interface.

Technical Discussion¶

See the documentation under VELO_SLIP boundary condition for a description of the nature of this boundary condition.
An important caveat when using this boundary condition to relax no-slip in the vicinity of the interface is that it relaxes all constraints on the velocities in the region. This includes the constraint to keep fluid from passing through the substrate boundary. For this region, it is usually also necessary to use a impenetrability condition, VELO_NORMAL for example, in conjunction with this boundary condition for appropriate results.

References¶

No References.

VELO_SLIP_ELECTROKINETIC¶

BC = VELO_SLIP_ELECTROKINETIC SS <bc_id> <float1> <float2>

Description / Usage¶

(SIC/ROTATED MOMENTUM)

This boundary condition allows for slip between the fluid and a solid boundary due to electrokinetic effects on the charged solid wall. The user provides the following parameters: zeta potential at the wall and permittivity of the fluid.

VELO_SLIP_ELECTROKINETIC	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	\(\varepsilon\), absolute permittivity of the fluid.
<float2>	\(\zeta\), the surface potential of solid boundary. It is referred to as the zeta potential.

Examples¶

Following is a sample card:

BC = VELO_SLIP_ELECTROKINETIC SS 10 1.e-5 1.e-2

Technical Discussion¶

The general form of this boundary condition is

where \(\varepsilon\) is the absolute permittivity of the medium, \(\zeta\) is the zeta potential, \(E_t\) is the electric field tangent to the solid surface, and \(v_s\) is the slip velocity.

VELO_SLIP_ELECTROKINETIC3D¶

BC = VELO_SLIP_ELECTROKINETIC3D SS <bc_id> [floatlist]

Description / Usage¶

(SIC/ROTATED MOMENTUM)

This is a 3D generalization of the VELO_SLIP_ELECTROKINETIC boundary condition. It is similar to VELO_TANGENT_3D except the slip velocity is calculated based on Helmholtz-Smulkowski relation. This boundary condition allows for slip between the fluid and a solid boundary due to electrokinetic effects on the charged solid wall. The user provides the following parameters: zeta potential at the wall, permittivity of the fluid and.

VELO_SLIP_ELECTROKINETIC3D	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	\(\varepsilon\), absolute permittivity of the fluid.
<float2>	\(\zeta\), the surface potential of solid boundary. It is referred to as the zeta potential.
<float3>	\(t_x\), the x-component of a unit normal vector tangent to the surface; this vector must be tangent at all points on the surface. The direction of the imposed tangential velocity component is n × t with n the outwardpointing normal.
<float4>	\(t_y\), the y-component of a unit normal vector tangent to the surface; this vector must be tangent at all points on the surface. The direction of the imposed tangential velocity component is n × t with n the outwardpointing normal.
<float5>	\(t_z\), the z-component of a unit normal vector tangent to the surface; this vector must be tangent at all points on the surface. The direction of the imposed tangential velocity component is n × t with n the outwardpointing normal.

Examples¶

Following is a sample card:

BC = VELO_SLIP_ELECTROKINETIC3D SS 10 1.e-5 1.e-2 0. 0. 1.

Technical Discussion¶

The general form of this boundary condition is

where \(\varepsilon\) is the absolute permittivity of the medium, \(\zeta\) is the zeta potential, \(E_t\) is the electric field tangent to the solid surface, and \(v_s\) is the slip velocity.

VELO_TANGENT_SOLID¶

BC = VELO_TANGENT_SOLID SS <bc_id> <integer1> <integer2>

Description / Usage¶

(SIC/ROTATED MOMENTUM)

This boundary condition sets the tangential fluid velocity component at a fluid/solid interface to the tangential velocity component of the solid material. The latter includes any motion of the stress-free state. This boundary condition is applicable only to twodimensional problems and is normally used in conjunction with the Total Arbitrary Lagrangian/Eulerian algorithm in Goma (See GT-005.3).

Definitions of the input parameters are as follows:

VELO_TANGENT_SOLID	The name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer1>	The element block id defining the solid phase adjacent to <bc_id>.
<integer2>	The element block id defining the liquid phase adjacent to <bc_id>.

Examples¶

The following is an example of this card

BC = VELO_TANGENT_SOLID SS 10   2 1

In this case, sideset 10 is an internal sideset between two separate materials, the solid material in element block 2 and the liquid material in element block 1.

Technical Discussion¶

The boundary condition being applied is the strong integrated condition:

where \(v_m\) is the fluid velocity, \(v_{sfs}\) is the velocity of the solid material stress-free-state (usually solid-body translation, or rotation..see Advected Langragian Velocity card) including the motion of the deformed coordinates, and t is the vector tangent to the side set. \(F_m\) is the deformation gradient tensor and the time derivative term is the motion of the deformed state tangential to the surface in question.

This condition is advocated for use with the TALE algorithm (see GT-005.3).

VELO_SLIP_SOLID¶

BC = VELO_SLIP_SOLID SS <bc_id> <integer_list> <float1> [integer3, float2]

Description / Usage¶

(WIC/ROTATED MOMENTUM)

This boundary condition is similar in function to the VELO_SLIP condition in that it permits a tangential velocity in a fluid phase to be proportional to the shear stress at the boundary. This boundary condition allows for this type of slip to occur at the interface between a fluid material and a LAGRANGIAN or TALE solid material. The velocity of the solid substrate is obtained automatically from the motion of the solid material, including advection of the stress-free state. As in the case of the VELO_SLIP condition, this condition also permits the user to vary the slip coefficient depending upon the distance from a specified point in the mesh. The variable slip model can only be used in two-dimensional problems.

The <integer_list> has two values; the definitions of the input parameters and their significance in the boundary condition parameterization is described below:

VELO_SLIP_SOLID	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain. This should be an internal sideset defined at the interface between solid and liquid material blocks.
<integer1>	The element block id defining the solid material phase.
<integer2>	The element block id defining the liquid material phase.
<float1>	\(\beta\), the slip coefficient. The inverse of \(\beta\) defines the scaling between stress and slip. Hence, for small values of \(\beta\), large shear stresses are needed for a given amount of slip, and conversely, for large values of \(\beta\), the amount of stress needed for the same degree of slip decreases (see below for a more rigorous description).
[integer3]	\(N_{cl}\), a single-node node set identification number. When the variable coefficient slip relation is used, distance is measured relative to this node (see discussion below). Normally, this node set represents the location of the dynamic contact line. Note that this option is generally only used in two-dimensional simulations.
[float2]	\(\alpha\), the distance scale in the variable slip model (see the discussion below). Both \(N_{cl}\) and \(\alpha\) should be present to activate the variable slip model.

Examples¶

The following is a sample card:

BC = VELO_SLIP_SOLID SS 20    2 1 0.001 0.0 4 0.01

This boundary condition sets the slip coefficient between solid material 2 and liquid material 1 to be 0.001 except in the vicinity of the nodeset 4 (a single node) where the variable model is used.

Technical Discussion¶

The general form of this boundary condition is

where \(\tau\) is the deviatoric portion of the fluid stress tensor, \(\beta\) is the Navier slip coefficient and \(v_{sfs}\) is the velocity of the solid surface stress-free state, with \(F_m\) the deformation gradient tensor; this motion includes any rigid solid body motion and any superimposed deformation velocity.

It is worthwhile noting that, unlike the VELO_SLIP condition, this condition is actually a rotated condition. It is applied to the tangential component of the rotated momentum equations weakly. This means that the normal component of the momentum equation is not affected by this boundary condition. Normally, some sort of no-penetration condition must accompany this boundary condition for this reason.
The reader is referred to the documentation of the variable slip coefficient model to apply slip near contact lines under the VELO_SLIP boundary condition.

DISCONTINUOUS_VELO¶

BC = DISCONTINUOUS_VELO SS <bc_id> <char_string> <integer1> <integer2>

Description / Usage¶

(SIC/MOMENTUM)

This boundary condition card, used to set the normal component of mass averaged velocity at an interface, specifies that the net flux of the last component in a nondilute mixture across an internal interface, is equal to zero. The condition only applies to interphase mass, heat, and momentum transfer problems applied to nondilute material phases with discontinuous (or multivalued) variables at an interface, and it must be invoked on fields that employ the Q1_D or Q2_D interpolation functions to “tie” together or constrain the extra degrees of freedom at the interface in question.

Definitions of the input parameters are as follows:

DISCONTINOUS_VELO	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<char_string>	A character string identifiying the condition to be applied on the liquid phase relative to the gas phase. EVAPORATION DISSOLUTION - not currently valid. Note, this parameter replaces the boundary condition EVAPORATION_VELO.
<integer1>	Element block id of liquid or high density phase.
<integer2>	Element block id of gas or low density phase.

Examples¶

Following is a sample input card that applies this BC on the block 1 side of side set 7, the liquid side; the block 2 side is the gas side.

BC = DISCONTINUOUS_VELO SS 7 EVAPORATION 1 2

Technical Discussion¶

The DISCONTINUOUS_VELO boundary condition applies the following equation:

It specifies the diffusive flux of the last species in the mechanism, i.e., the one for which no explicit continuity equation exists, to be equal to zero. This is done via a strong integral condition applied to one side of the interface, the “+” side of the interface. This boundary condition, combined with the KINEMATIC_SPECIES and KINEMATIC_DISC boundary conditions, implies that the diffusive flux of the last species on both sides of the boundary is equal to zero.

The DISCONTINUOUS_VELO boundary condition requires an evaluation of the derivative of the species mass fraction at the interface. Thus, the mesh convergence properties of the algorithm are reduced to O( h ). Also, discretization error must interfere with the total mass balance across a phase, since the expression for \(j_i^+\) is substituted for in some places, the YFLUX_SPECIES boundary condition, but used in the DISCONTINUOUS_VELO boundary condition.

HYDROSTATIC_SYMM¶

BC = HYDROSTATIC_SYMM

Description / Usage¶

(WIC/VECTOR MOMENTUM)

No longer supported in GOMA. Do not use.

Examples¶

No Example.

Technical Discussion¶

No Discussion.

References¶

No References.

FLOW_PRESSURE¶

BC = FLOW_PRESSURE SS <bc_id> <float>

Description / Usage¶

(WIC/VECTOR MOMENTUM)

This boundary condition card is used to set a constant value of pressure on a boundary. Most often this condition is used to set an upstream or downstream pressure over a fully-developed inflow/outflow boundary.

Definitions of the input parameters are as follows:

FLOW_PRESSURE	Boundary condition name.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float>	\(P_{ex}\), the applied pressure. Positive values imply compressive forces on the fluid, negative values imply tensile forces.

Examples¶

The following sample input card will impose a constant compressive pressure force on the boundary defined by sideset 23:

BC = FLOW_PRESSURE SS 23   5.0

Technical Discussion¶

The actual boundary condition that is applied to the fluid is given as follows:

where n is the outward normal vector to the boundary, T is the total fluid stress tensor, and P is the applied pressure equal to <float1> above. From this the user should be able to deduce the appropriate sign for his/her pressure value.

This boundary condition is a weak integrated condition implying that it is added to all three components of the fluid momentum equation prior to rotation of equations or application of strongly enforced conditions or Dirichlet conditions.
The astute user who is also well-versed in finite element formulations and terminology will recognize that this boundary condition is providing a value for the boundary condition term that appears after application of the divergence theorem to the weighted fluid momentum residual equations. Hence, imposing a value of zero for <float1> is exactly equivalent to saying nothing at all about the fluid velocity at a boundary.
This boundary condition is found predominantly in two applications. First, setting the external pressure imposed on a free surface, and second, providing the driving force for flow by being imposed on an inflow or outflow fully-developed boundary. In this latter role, the usual procedure is to apply the FLOW_PRESSURE condition while strongly enforcing a zero condition on the velocity components transverse to the boundary. For boundaries parallel to one of the principle coordinate directions, Dirichlet conditions can be used to set these transverse components. For other inflow or outflow boundaries, it is suggested that the VELO_TANGENT and VELO_TANGENT_3D cards be employed instead.
This boundary condition is very useful when working with non-Newtonian models where the inlet velocity field is apt to be complicated and hard to determine a priori. By imposing a pressure at the inflow with this card, the non-Newtonian inlet velocity profile will be determined implicitly. Augmenting conditions can then be used to couple the imposed pressure to the average flow rate over the boundary for an even more advanced capability.

FLOW_STRESSNOBC¶

BC = FLOW_STRESSNOBC SS <bc_id> <float> [integer]

Description / Usage¶

(WIC/VECTOR MOMENTUM)

This boundary condition card applies the free outflow boundary condition developed by Papanastasiou, et.al. (1992) on the fluid momentum with the option of setting the pressure level. It is appropriate only for outflow boundaries where it is inappropriate to use natural boundary conditions or FLOW_PRESSURE-class boundary conditions. It is only supported for generalized Newtonian fluid constitutive equations.

Definitions of the input parameters are as follows:

FLOW_STRESSNOBC	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float>	\(P_{applied}\), the applied pressure.
[integer]	An optional parameter. blank/-1 the pressure in the normal stress is replaced by \(P_{applied}\). ≠ –1 the pressure in the solution vector is retained in the normal stress.

Examples¶

Following is a sample card:

BC = FLOW_STRESSNOBC SS 10   1.0 -1

Here the boundary condition is applied to sideset 10 with a constant pressure of 1.0 required.

Technical Discussion¶

The finite element formulation of the fluid momentum equations generates boundary integrals of the form:

where P is the isotropic pressure and \(\tau\) the viscous stress. Often this boundary term is left off entirely on a particular boundary with the result that a zero normal force is applied implicitly. These are referred to as imposing a “natural” boundary conditions. Alternatively, this integral might be included but with the integrand replaced by an known value of force. This is the concept behind the FLOW_PRESSURE and FLOW_HYDROSTATIC boundary conditions.

However, both types of boundary conditions imply that something is known about the stress and, by association, the velocity field on the boundary. It is often the case that outflow boundaries are present where it is difficult to provide this information. A prime example is the outflow of a fluid jet accelerating downward due to gravity. In this case, the downward velocity field is still developing at this boundary so it is problematic to specify a stress value. Other examples include imposing conditions at a “truncated” outflow where the exiting fluid is still developing.

The FLOW_STRESSNOBC seeks to remedy this problem. Formulationally, the boundary term as written above is included as just another term dependent upon solution degrees of freedom. This permits the pressure and velocity gradients on the boundary to float as needed so that one does not need to say anything about the stress or pressure on the boundary.

Now strictly speaking, the ellipticity of the viscous flow equations suggests that this operation should result in an ill-posed problems. Elliptic equations by their very nature require that something be said about every boundary in the problem. However, in the case of outflow boundaries it appears that this restriction can be relaxed in certain circumstances with good results. Papanastasiou, et.al., (1997), Renary (1997), Griffiths (1997) and Sani and Gresho (1994) discuss this.

The boundary condition does permit that the pressure value be fixed while the viscous stress is allowed to float. This is done by setting the optional parameter to -1 and supplying the pressure value as \(P_{applied}\). When this is done depends upon circumstance. Note that this is distinctly different from setting a normal stress component using FLOW_PRESSURE.
As noted above, this boundary condition is currently implemented only for generalized Newtonian fluid models. Polymeric fluid models will not work with it.

References¶

Griffiths, D.F., “The ‘no boundary condition’ outflow boundary condition,” IJNMF, 24, 393-411, (1997)

Papanastasiou, T. C., N. Malamataris, and K. Ellwood, “A New Outflow Boundary Condition”, IJNMF, 14, 587-608, (1992).

Renardy, M., “Imposing ‘NO’ boundary conditions at outflow: Why does this work?” IJNMF, 24, 413-417, (1997).

Sani, R.L., and P.M. Gresho, “Resume and remarks on the open boundary condition minisymposium,” IJNMF, 18, 983-1008, (1994).

FLOW_GRADV¶

BC = FLOW_GRADV SS <bc_id> <float> [integer]

Description / Usage¶

(WIC/VECTOR MOMENTUM)

This boundary condition card stipulates a vanishing normal velocity gradient on a boundary with the option of setting the pressure level.

Definitions of the input parameters are as follows:

FLOW_GRADV	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float>	\(P_{applied}\), the applied pressure.
[integer]	An optional parameter.
	blank/-1	the pressure in the normal stress is replaced by \(P_{applied}\).
	≠ –1	the pressure in the solution vector is retained in the normal stress.

Examples¶

The sample input card:

BC = FLOW_GRADV SS 15   0.0

sets the gradient of velocity normal to sideset 15 to zero. A pressure value of zero is used in the boundary condition.

BC = FLOW_GRADV SS 15   0.0   1.0

In the preceding example, the pressure value used is obtained from the solution itself.

Technical Discussion¶

This boundary condition is related in form and formulation to the FLOW_STRESSNOBC boundary condition in that it includes terms for the boundary integrals that appear in the momentum equation after application of integration by parts and the divergence theorem. In this boundary condition, the following integral is included with the momentum equation:

where \(\mu\) is the viscosity of a Newtonian or generalized Newtonian fluid. As in the case of the FLOW_STRESSNOBC condition the preceding integral appears as a function of pressure and velocity unknowns as any other term.

The pressure term in the preceding may be replaced by a fixed, imposed pressure value. This is done by setting the optional input integer to -1 and providing the imposed value in \(P_{applied}\) ; otherwise, the value set in \(P_{applied}\) is ignored.

FLOW_PRESS_USER¶

BC = FLOW_PRESS_USER

Description / Usage¶

(WIC/VECTOR MOMENTUM)

This boundary condition has been deprecated in favor of the PRESSURE_USER boundary condition; use the latter instead.

Examples¶

No Examples.

Technical Discussion¶

No Discussion.

References¶

No References.

FLOW_HYDROSTATIC¶

BC = FLOW_HYDROSTATIC SS <bc_id> <float_list>

Description / Usage¶

(WIC/VECTOR MOMENTUM)

This boundary condition allows the user to impose a pressure force that varies linearly with position over the boundary. It functions in much the same manner as the FLOW_PRESSURE boundary condition except that more variability is allowed in the imposed pressure. As the name implies, this boundary condition is most often used to impose hydrostatic pressure profiles in problems in which gravitational forces play a role.

The <float_list> has four values to be specified; definitions of the input parameters are as follows:

FLOW_HYDROSTATIC	Boundary condition name.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	\(\delta P_x\), the pressure variation in x-direction.
<float2>	\(\delta P_y\), the pressure variation in y-direction.
<float3>	\(\delta P_z\), the pressure variation in z-direction.
<float4>	\(P_0\), the pressure value at the coordinate point (0,0,0). This serves as a means of establishing a datum and it is not required that (0,0,0) lie on the sideset.

Examples¶

Following is a sample card:

BC = FLOW_HYDROSTATIC SS 15   0.0 0.0 -1.5 10.0

This card will impose a pressure profile on side set 15 so that the pressure decreases by 1.5 as the z coordinate increases by one unit. At the point, (0,0,0) the pressure imposed is 10.0. Note that (0,0,0) does not necessarily have to be on side set 15.

Technical Discussion¶

The mathematical form of the boundary condition imposed by this card is as follows:

where n is the outward normal vector to the boundary, T is the total fluid stress tensor, and x, y, z are the global coordinate positions.

Like the FLOW_PRESSURE conditions, this is a weakly integrated condition and the comments appearing with that card apply equally well here.
Most often this boundary condition is used in problems in which gravity is present. Under these circumstances, the pressure profile across a fully-developed flow inlet is not constant but varies according to hydrostatic head. Hence, the FLOW_PRESSURE condition cannot be used to provide the inlet pressure. Instead, this card is used with the variation in the pressure being imposed according to the direction of gravity. Thus, some if not all of \(\delta P_x\), \(\delta P_y\), or \(\delta P_z\) will be functions of gravity and the fluid density.
It is true that this variation could be determined automatically by Goma from its known values for density and gravitational direction. But for a variety of reasons, this may not always be the best option. Instead, the user is allowed to vary the pressure on a boundary independently of the density and gravitational forces set elsewhere in the material file. If consistency is important in the problem at hand, then the user is cautioned to be consistent.
The input parameter \(P_0\) as noted above serves as a datum to the relationship. In theory, it is the pressure value that would be computed at the point (0,0,0), but in reality it is chosen to impose a known pressure at some point in the domain.

References¶

No References.

FLOWRATE¶

BC = FLOWRATE SS <bc_id> <float> <float | char_string>

Description / Usage¶

(WIC/VECTOR MOMENTUM)

This boundary condition allows the user to specify a single value for the volumetric flowrate of material across an inflow (or outflow) boundary. The pressure and velocity fields on this boundary are then computed implicitly by Goma.

Definitions of the input parameters are as follows:

FLOWRATE	Boundary condition name.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float>	flowrate, a parameter fixing the value of volumetric flowrate across this boundary. For two-dimensional CARTESIAN simulations, this value should be per unit distance in the out-of-plane coordinate. For CYLINDRICAL and SWIRLING coordinate systems, this flowrate value should include integration in the azimuthal direction.
<float\|char_string>	This parameter can either be a <float> or a <char_string>.
	float	\(P_{guess}\), an initial guess for the pressure on the inlet
	char_string	read, indicating that the initial guess for the pressure file should be read from the ASCII file identified on the GUESS file card.

Examples¶

Specifying the average velocity on the inlet to a tube of radius 1.0:

BC = FLOWRATE SS 10 3.1415 10.0

Since the radius is 1.0, the area of the surface is 3.1415 so the volumetric flowrate must be specified as shown. An initial pressure guess of 10.0 is also supplied. Note this does not specify the pressure on the boundary as the final value will generally be different than specified here.

Continuing in the flowrate by reading the last pressure value from GUESS file:

BC = FLOWRATE SS 10 3.2 read

Technical Discussion¶

The requirement that is imposed by this boundary condition is the following integral:

where U is the flowrate value supplied on the card. It is imposed by the addition of a Lagrange multiplier unknown on the boundary in question which will be determined as a part of the solution process. For Newtonian and generalized Newtonian models, the value of the multiplier is the inverse of the pressure value on the boundary. Thus, a boundary condition nearly identical to a FLOW_PRESSURE condition is applied to the sideset, but it takes as its pressure the value of the inverse of the Lagrange multiplier unknown as it is computed.

The augmenting condition capability in Goma is used to impose the above integral. When the boundary condition is invoked, an augmenting condition of the appropriate type is automatically created. Its associated degree of freedom is the Lagrange multiplier. During the iteration sequence, the user will see updates and residuals for this augmenting condition.

Originally, the initial guessed value for the pressure over the side set is read from the float value specified on this card, or from the GUESS file (if the parameter read is specified on this card). However, it can also be read from an EXODUS II database file. This is the same file the rest of the solution vector is read from if the problem is being restarted from a previous computation. If a value for the augmenting condition is present in this EXODUS II file, it will be read in. This value will override the float value specified on this card. The initial guess may still be read from the ASCII GUESS file by specifying read on the Initial Guess card and on the Augmenting Conditions Initial Guess card.

References¶

No References.

PRESSURE_USER¶

BC = PRESSURE_USER SS <bc_id> <float_list>

Description / Usage¶

(WIC/VECTOR MOMENTUM)

This boundary condition allows the user to specify an arbitrary functional form for the pressure field on a boundary via a user-defined subroutine. The boundary condition is identical in form to the FLOW_PRESSURE and FLOW_HYDROSTATIC conditions, but whereas the latter conditions have constant and linear spatial dependencies for the pressure, this boundary condition allows for any dependency, including dependencies on other degrees of freedom and time.

Definitions of the input parameters are as follows:

PRESSURE_USER	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float_list>	A list of float values separated by spaces which will be passed to the user-defined subroutine so the user can vary the parameters of the boundary condition. This list of float values is passed as a one-dimensional double array to the appropriate C function.

Examples¶

The following is a sample input card:

BC = PRESSURE_USER SS 10 0.0 3.0 0.5

Technical Discussion¶

Frequently, it is desired to be able to set a pressure on a boundary that is more complicated than constant or linear; this boundary condition is used for this purpose. By modifying a function in user_bc.c (fn_dot_T_user), any functional dependence of pressure can be installed. This dependence may entail a more complicated spatial dependence, variability in time, and/or dependence on other degrees of freedom.
An example is supplied in fn_dot_T_user that illustrates how this boundary condition can be used to set a sinusoidal-type of spatial dependence. A similar function could be used to set a temporal sinusoidal variation. The only caveat is that when inserting a function, it is very important that the sensitivities of the function with respect to position (and other degrees of freedom if they exist) be added to the array d_func. This does not apply to the time variable however.
Like FLOW_PRESSURE and FLOW_HYDROSTATIC, this boundary condition is a weakly integrated condition. Therefore, it is additive with other weak conditions, but is superseded by strong conditions or Dirichlet conditions.

CONT_TANG_VEL¶

BC = CONT_TANG_VEL SS <bc_id>

Description / Usage¶

(SIC/MOMENTUM)

This boundary condition card enforces continuity of tangential velocity between two phases with discontinuous velocity treatment. The condition only applies to interphase mass, heat, and momentum transfer problems with discontinuous (or multivalued) variables at an interface, and it must be invoked on fields that employ the Q1_D or Q2_D interpolation functions to “tie” together or constrain the extra degrees of freedom at the interface in question.

Definitions of the input parameters are as follows:

CONT_TANG_VEL	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.

Examples¶

The following is a sample card:

BC = CONT_TANG_VEL SS 10

Technical Discussion¶

No Discussion.

CONT_NORM_VEL¶

BC = CONT_NORM_VEL SS <bc_id>

Description / Usage¶

(SIC/MOMENTUM)

This boundary condition card is similar to the VELO_NORM_DISC card except that it enforces a continuous normal velocity component in a discontinuous boundary field. The condition only applies to interphase mass, heat, and momentum transfer problems with discontinuous (or multivalued) variables at an interface, and it must be invoked on fields that employ the Q1_D or Q2_D interpolation functions to “tie” together or constrain the extra degrees of freedom at the interface in question.

Definitions of the input parameters are as follows:

CONT_NORM_VEL	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.

This boundary condition is typically applied to multicomponent two-phase flows that have rapid mass exchange between phases, rapid enough to induce a diffusion velocity at the interface, and to thermal contact resistance type problems. The best example of this is rapid evaporation of a liquid component into a gas.

Examples¶

The following is a sample card:

BC = CONT_NORM_VEL SS 10

Technical Discussion¶

No Discussion.

References¶

No References.

VNORM_LEAK¶

BC = VNORM_LEAK SS <bc_id> <float1> <float2>

Description / Usage¶

This boundary condition card is used to specify a normal velocity boundary condition with mass transfer on momentum equations. The flux quantity is specified on a per mass basis so the heat and mass transfer coefficients are in units of L/t.

Definitions of the input parameters are as follows:

VNORM_LEAK	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	\(h_i\), mass transfer coefficient for bulk fluid (n+ \(1^{th}\) species).
<float2>	\(y^0_i\), driving force concentration in external phase.

Examples¶

The following is a sample input card:

BC = VNORM_LEAK SS 1   1. 0.

Technical Discussion¶

This card is the equivalent of KIN_LEAK except it is solved for the normal component of the momentum equation. Similar to KIN_LEAK, this flux provides an overall mass transfer balance at an interface. Please refer to the technical discussion of KIN_LEAK boundary card.

CAPILLARY¶

BC = CAPILLARY SS <bc_id> <float_list> [integer]

Description / Usage¶

(WIC/VECTOR MOMENTUM)

This boundary condition card is used to apply capillary forces (surface tension) to the momentum equation on a free-surface.

Definitions of the input parameters are as follows:

CAPILLARY	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	\(\sigma\), surface tension or capillary term multiplier. IMPORTANT NOTE: if no Surface Tension card appears in the material file, this parameter is the surface tension value used here. If Surface Tension is set in the material file, however, this float value will multiply the surface tension value from the material file prior to it’s application in this boundary condition. Best practice is to set this parameter to 1.0 and set the surface tension value in the material file.
<float2>	\(P_{ex}\), the external applied isotropic pressure on the free surface.
<float3>	\(P_r\), deprecated capability. Always set to zero.
[integer]	Optional integer value indicating the element block id from which to apply the boundary condition. This is used to force the capillary stresses to be applied from within a phase where the momentum equations are defined.

Examples¶

Following is a sample card:

BC = CAPILLARY SS 12   1.0 10.0 0.0

This card specifies that capillary forces be applied to the free surface on side set 12. If a surface tension material parameter value or model is supplied, this is the surface tension value used. If not, the surface tension value used is 1.0. An external isotropic pressure of 10.0 is applied from the surrounding environment.

Technical Discussion¶

One of the primary characteristics of a free-surface is the presence of surface tension-related forces. This boundary condition permits application of such forces. The forces on the fluid at the free-surface are set via the following relation:

where n is the outward normal to the surface, T is the fluid stress tensor, \(P_{ex}\) is the external applied pressure described above, H is the surface curvature defined as, H = –\(\Delta_s\) ⋅ n ⁄ 2, \(\sigma\) is the surface tension, and \(\Delta_s\) is the surface divergence operator defined as \(\Delta_s^f\) = (I – nn) ⋅ \(\Delta\) f .

Typical usage of this boundary condition is in conjunction with a KINEMATIC boundary condition. The latter enforces no penetration of fluid through a free surface by deforming the mesh and this boundary condition acts on the fluid momentum equation to enforce the capillary jump condition given above.
No end of confusion results from use of this card primarily because of overloading the surface tension parameter. To reiterate, the value for surface tension that appears on this card is the actual (constant) value of surface tension that is used if a surface tension model has NOT been specified explicitly in the material file. If such a model has been identified, the surface tension parameter in the CAPILLARY card is a multiplier to the surface tension. The best practice is to simply always use 1.0 for this parameter and set the surface tension in the material file.
The optional (integer) element block ID corresponds to the material numbers given in the Problem Description section of the input file.

CAP_REPULSE¶

BC = CAP_REPULSE SS <bc_id> <float_list> [mat_id]

Description / Usage¶

(WIC/VECTOR MOMENTUM)

This card functions much in the same way as the CAPILLARY card. It imposes surface tension forces on free-surfaces. The addition to this card, however, is that in the vicinity of a specified planar boundary, an additional repulsive force is added to the surface tension force. This force is directed away from the planar surface and increases in proportion to 1/ \(r^2\) as the free-surface approaches the planar surface. This condition can be used to contend with the difficult problem of fluid/solid contact in an approximate way. This boundary condition is only applicable to two-dimensional problems; trying to apply it in a three-dimensional problem will cause an error.

There are seven values in the <float_list>; definitions of the input parameters are as follows:

CAP_REPULSE	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	\(\sigma\), the surface tension value or a multiplier for the capillary effect. See the important caveat under the CAPILLARY card regarding the use of this parameter when a surface tension value is supplied in the material file.
<float2>	\(P_{ex}\), the applied external pressure field on the free surface.
<float3>	\(P_{rep}\), the coefficient on the surface repulsion term. This parameter should have units of (ML/ \(T^2\)). See below for an exact description of the surface repulsion term.
<float4>	a, the sensitivity with respect to x-coordinate (the a coefficient) of the plane surface that is repelling the free surface sideset.
<float5>	b, the sensitivity with respect to y-coordinate (the b coefficient) of the plane surface that is repelling the free surface sideset.
<float6>	c, the sensitivity with respect to z-coordinate (the c coefficient) of the plane surface that is repelling the free surface sideset.
<float7>	d, the constant d coefficient of the plane surface equation that is repelling the free surface sideset.
[mat_id]	In the case of a surface node shared by more than one material, this optional integer parameter allows the user to specify which material the condition will be applied in. This is rarely used.

Examples¶

Following is a sample card:

BC = CAP_REPULSE SS 24 1.0 0.0 0.1 1. 1. 0. 2.

applies a standard capillary surface tension pressure jump condition to side set 24, except as the free surface approaches the plane surface defined by a solution to the equation x + y = -2.0.

Technical Discussion¶

This boundary condition applies the following force term to the fluid momentum equation:

which is almost identical to the force applied by the CAPILLARY card. The only difference is the last term on the right in which d is the normal distance from a given point on the free-surface side set and the planar surface defined by the equation:

CAP_RECOIL_PRESS¶

BC = CAP_RECOIL_PRESS SS <bc_id> <float_list>

Description / Usage¶

(WIC/VECTOR MOMENTUM)

This boundary condition calculates the surface recoil from an evaporating metal alloy component or water.

There are seven values in the <float_list>; definitions of the input parameters are as follows:

CAP_RECOIL_PRESS	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	This float is currently disabled.
<float2>	This float is currently disabled.
<float3>	Temperature at which the metal alloy begins to boil.
<float4>	Liquidus temperature of metal alloy.
<float5>	Reference temperature.
<float6>	Conversion scale for pressure.
<float7>	Conversion scale for temperature.

Examples¶

The following is a sample input card:

BC = CAP_RECOIL_PRESS SS 1   0.0 0.0 3000.0 1623.0 0.0 1.0 1.0

Technical Discussion¶

Currently this boundary condition has coefficients for only iron and water. Several required pieces of information to use this boundary condition are not in final form, and the user can expect future changes and improvements. This boundary condition is designed for use with Q_LASER_WELD.

References¶

No References.

ELEC_TRACTION¶

BC = ELEC_TRACTION SS <bc_id> <integer> <float>

Description / Usage¶

(WIC/VECTOR MOMENTUM)

This boundary condition card is used to add to the momentum equation the electric, or Maxwell, stress at a free-surface. Definitions of the input parameters are as follows:

ELEC_TRACTION	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer>	Integer value indicating the element block ID from which to apply the boundary condition.
<float>	A term-multiplier.

Since this boundary condition only adds the electric stress, it is commonly used with one of the CAPILLARY, CAP_RECOIL_PRESS or CAP_REPULSE boundary conditions, viz. the capillary stress must be added separately.

Examples¶

For a system consisting of an insulating liquid (element block ID 1) and an insulating, passive gas (element block ID 2) with a free-surface designated by side set 12, the following is a sample usage:

BC = ELEC_TRACTION SS 12 1 1.0

BC = ELEC_TRACTION SS 12 2 1.0

BC = CAPILLARY SS 12 1.0 0.0 0.0 1

The first and second lines adds the electric stress due to the electric field in the liquid and gas phases, respectively. The third line adds the capillary stress due to surface tension. IMPORTANT NOTE: the optional element block ID argument to the CAPILLARY card is used to make sure that the capillary stress is added from within a phase where the momentum equations are defined. The same holds for the KINEMATIC boundary condition.

Technical Discussion¶

This boundary condition adds the electric, or Maxwell, stress contribution to the traction condition. To use this boundary condition there must be a VOLTAGE equation present in one or both of the materials neighboring the interface, i.e., one or both of the neighboring materials must be a dielectric. The electrical permittivity of each dielectric material must be supplied via the Electrical Conductivity card (yes, this is a kludge) in the material property file.

In its most general form, the traction condition is written

where T is the stress tensor, the superscripts ( o ) and ( i ) denote the outer and inner phases, n is a unit normal pointing into the outer phase, -H is the local mean curvature, and \(\sigma\) is the surface tension.

The stress tensor can be written as the sum of the mechanical stress \(T_m\) (e.g., the Newtonian stress tensor) and an electrical stress \(T_e\), viz. T = \(T_m\) + \(T_e\). The electric stress tensor provided through this boundary condition applies to incompressible, polarizable materials:

where \(\varepsilon\) is the electrical permittivity, E = – \(\Delta\) V is the electric field and V is the voltage or electric potential.

In expanded form, the traction condition becomes

The ELEC_TRACTION boundary condition is responsible for applying either the first or second terms on the right hand side (specified through the element block ID parameter) whereas the CAPILLARY (or related boundary condition) is responsible for the third and fourth terms.

The term multiplier supplied by the <float> input is used in the elec_surf_stress() function (mm_ns_bc.c) which applies the ELEC_TRACTION boundary condition. It is the etm function argument. The normal term multipliers couldn’t be used because this boundary condition can be applied from within a material that doesn’t have the momentum equations defined (or properly set).

CAP_ENDFORCE¶

BC = CAP_ENDFORCE NS <bc_id> <float_list>

Description / Usage¶

(SPECIAL/VECTOR MOMENTUM)

This boundary condition card adds surface tangent forces to the momentum equations at the endpoint of a free-surface. There are four values to be input for the < float_list>; definitions of the input parameters are as follows:

CAP_ENDFORCE	Name of the boundary condition (<bc_name>).
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	X-component of surface tangent vector at end point.
<float2>	Y-component of surface tangent vector at end point.
<float3>	Z-component of surface tangent vector at end point.
<float4>	Equilibrium surface tension value. (See Technical Discussion.)

This condition need only be applied at the intersection of outflow or inflow surfaces and the free-surface. The sign on the tangent vector depends on whether the computed tangent vector is facing inward or outward. This can be figured by t = n × k.

Examples¶

The following is a sample input card using several APREPRO variables:

BC = CAP_ENDFORCE NS 100   {sind(th2)} {-cosd(th2)} 0.0 {surf_tens}

Technical Discussion¶

The need for this boundary condition appears out of the formulation used to apply capillary forces to surfaces. The surface divergence theorem is used to simplify the curvature term in the capillary stress jump condition. This produces integrals of the form:

where C is the bounding curve of the capillary free surface, \(\sigma\) is the surface tension, \(\phi_i\) is a finite element shape function and m is a vector that is at once normal to the capillary surface and also normal to the curve C. It always points outward from the domain in question. While this is completely general for threedimensions, a surface can be reduced to a curve for two-dimensions and the divergence theorem still applies (for this boundary condition).

This card or the CAP_ENDFORCE_SCALAR is used in conjunction with the CAPILLARY card to complete (as indicated above) the treatment of capillarity conditions. It is only required when an inflow or outflow boundary intersects a free surface.
The CAP_ENDFORCE boundary condition is applied through function fapply_ST (in file mm_ns_bc.c). The boundary term is computed as the product of the surface tension supplied on this card (<float4>) and the value supplied on the Surface Tension card in the material file. When the latter card is missing, Goma defaults its value to 1.0.
This card was previously called SURFTANG for the surface tangent component of the capillary force. Old input decks can be updated simply by changing the name of the boundary condition without changing the parameters.

SURFTANG_EDGE¶

BC = SURFTANG_EDGE SS <bc_id1> <bc_id2> <float_list>

Description / Usage¶

(WIC/VECTOR MOMENTUM)

This boundary condition card is used to insert surface tension forces on an edge boundary defined by the primary and secondary sidesets. The direction of application of the surface tension ( \(\sigma\) ) is specified by the vector (defined by (< \(m_x\) >, < \(m_y\) >, < \(m_z\) >)). This card is the three-dimensional analog of the CAP_ENDFORCE card. It is often used at free-surface outflow boundaries if the outflow velocity is not set by a strong condition. This condition is an unrotated, weak integrated vector condition.

There are four values to be supplied in the <float_list>; definitions of the input parameters are as follows:

SURFTANG_EDGE	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id1>	The boundary flag identifier, an integer associated with <bc_type> that identifies the primary boundary location (side set in EXODUS II) in the problem domain. This side set is usually attached to a free surface.
<bc_id2>	The boundary flag identifier, an integer associated with <bc_type> that identifies the secondary boundary location (side set in EXODUS II) in the problem domain. The boundary condition is applied on the edge defined by the intersection of this side set with the primary side set.
<float1>	\(m_x\), the x-component of direction of application of surface tension force.
<float2>	\(m_y\), the y-component of direction of application of surface tension force.
<float3>	\(m_z\), the z-component of direction of application of surface tension force.
<float4>	a factor multiplying the surface tension value read from the material file when evaluating the surface integral imposed by this boundary condition.

Examples¶

The following is a sample input card:

BC = SURFTANG_EDGE SS 80 60   0. -1. 0. 1.

Technical Discussion¶

The need for this boundary condition appears out of the formulation used to apply capillary forces to surfaces in three-dimensions. The surface divergence theorem is used to simplify the curvature term in the capillary stress jump condition. This produces integrals of the form:

where C is the bounding curve of the capillary free surface, \(\sigma\) is the surface tension, \(\phi_i\) is a finite element shape function and m is a vector that is at once normal to the capillary surface and also normal to the curve C. It always points outward from the domain in question.

Most often this boundary condition appears at outflow boundaries of free-surfaces. It is applied along the edge where the free-surface intercepts the outflow plane. In this case, the m vector is normal to the outflow plane. If the outflow velocity is not strongly set by a Dirichlet condition or other strongly enforced condition, this boundary condition needs to be present so that a proper inclusion of all relevant surface tension terms is performed.

The <factor> parameter is provided to allow the user to independently vary the surface tension value associated with this term alone. The value for \(\sigma\) used in the preceding expression is the surface tension value obtained from the model specified in the material file multiplied by the value of <float>. Reasons for doing this are somewhat obscure but important to the practitioners of this art.

CAP_ENDFORCE_SCALAR¶

BC = CAP_ENDFORCE_SCALAR NS <bc_id> <float>

Description / Usage¶

(SPECIAL/VECTOR MOMENTUM)

This boundary condition card is very similar to the CAP_ENDFORCE card. It adds surface tangent forces to the momentum equations at the endpoint of a free-surface, but does not require specification of the surface tangent vector. The current free-surface tangent vector is used as the surface tangent vector. Definitions of the input parameters are as follows:

CAP_ENDFORCE_SCALAR	Name of the boundary condition (<bc_name>).
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float>	Equilibrium surface tension value. (See Technical Discussion.)

This condition need only be applied at the intersection of outflow or inflow surfaces and the free-surface.

Examples¶

The following is a sample input card:

BC = CAP_ENDFORCE_SCALAR NS 100   60.0

Technical Discussion¶

The need for this boundary condition appears out of the formulation used to apply capillary forces to surfaces. The surface divergence theorem is used to simplify the curvature term in the capillary stress jump condition. This produces integrals of the form:

where C is the bounding curve of the capillary free surface, \(\sigma\) is the surface tension, \(\phi_i\) is a finite element shape function and m is a vector that is at once normal to the capillary surface and also normal to the curve C. It always points outward from the domain in question. While this is completely general for threedimensions, a surface can be reduced to a curve for two-dimensions and the divergence theorem still applies (for this boundary condition).

This card or the CAP_ENDFORCE is used in conjunction with the CAPILLARY card to complete (as indicated above) the treatment of capillarity conditions. It is only required when an inflow or outflow boundary intersects a free surface.
The CAP_ENDFORCE_SCALAR boundary condition is applied through function fapply_ST_scalar (in file mm_ns_bc.c). The boundary term is computed as the product of the surface tension supplied on this card (<float>) and the value supplied on the Surface Tension card in the material file. When the latter card is missing, Goma defaults its value to 1.0.
This card was previously called SURFTANG_SCALAR for the surface tangent component of the capillary force. Old input decks can be updated simply by changing the name of the boundary condition without changing the parameters.

SURFTANG_SCALAR_EDGE¶

BC = SURFTANG_SCALAR_EDGE SS <bc_id1> <bc_id2> <float>

Description / Usage¶

(WIC/VECTOR MOMENTUM)

Like the SURFTANG_EDGE card, this boundary condition card is used to insert surface tension forces on an outflow edge boundary defined by the primary and secondary sidesets. In contrast to the SURFTANG_EDGE card, the direction of application of the surface tension ( \(\sigma\) ) is predetermined automatically as the binormal along the edge with respect to the outward facing normal of the primary sideset. This condition is also an unrotated, weak integrated vector condition. It should be used only in three-dimensional applications.

Definitions of the input parameters are as follows:

SURFTANG_EDGE_SCALAR	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database. Since it is an EDGE condition, it applies to a curve defined as the intersection of the primary and secondary sideset.
<bc_id1>	The boundary flag identifier, an integer associated with <bc_type> that identifies the primary boundary location (side set in EXODUS II) in the problem domain. This side set is used in defining the edge and the local vector basis (normal, tangent, binormal) and is usually attached to a free surface.
<bc_id2>	The boundary flag identifier, an integer associated with <bc_type> that identifies the secondary boundary location (side set in EXODUS II) in the problem domain. It is used in defining the edge and the local vector basis (normal, tangent, binormal).The boundary condition is applied on the edge defined by the intersection of this side set with the primary side set.
<float>	A factor multiplying the surface tension value read from the material file when evaluating the surface integral imposed by this boundary condition.

Examples¶

The following is a sample input card:

BC = SURFTANG_EDGE_SCALAR SS 5 10 1.0

applies the boundary integral (see the Technical Discussion) along the curve described by the intersection of side sets 5 and 10. The value for surface tension in the material file is used unmodified since the multiplying factor is 1.0.

Technical Discussion¶

The need for this boundary condition appears out of the formulation used to apply capillary forces to surfaces in three-dimensions. The surface divergence theorem is used to simplify the curvature term in the capillary stress jump condition. This produces integrals of the form:

where C is the bounding curve of the capillary free surface, \(\sigma\) is the surface tension, \(\phi_i\) is a finite element shape function and m is the outward binormal vector to the curve C with respect to the normal of the primary side set.

Most often this boundary condition appears at outflow boundaries of free surfaces. It is applied along the edge where the free surface intercepts the outflow plane. If the outflow velocity is not strongly set by a Dirichlet condition or other strongly enforced condition, this boundary condition needs to be present so that a proper inclusion of all relevant surface tension terms is performed.

The <factor> parameter is provided to allow the user to independently vary the surface tension value associated with this term alone. The value for \(\sigma\) used in the preceding expression is the surface tension value obtained from the model specified in the material file multiplied by the value of <float>. Reasons for doing this are somewhat obscure but important to the practitioners of this art.

FILL_CA¶

BC = FILL_CA SS <bc_id> <float>

Description / Usage¶

(WIC/VECTOR MOMENTUM)

This boundary condition is used to impose a contact angle on a boundary when using Level Set Interface Tracking.

A description of the input parameters follows:

FILL_CA	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float>	\(\theta\), the contact angle imposed, in degrees.

Examples¶

An example:

BC = FILL_CA SS 10 30.0

Technical Discussion¶

This boundary condition must be used in conjunction with the VELO_SLIP_FILL boundary condition. This latter condition permits the fluid to slip in the vicinity of the contact line. The FILL_CA acts by imposing a force on the momentum equation. The size of this force is more or less in proportion between the actual contact angle on the boundary and the value specified on the card. This force is applied as a weakly integrated condition and if the VELO_SLIP_FILL condition is not present, the FILL_CA will be overwritten and ipso facto absent.

References¶

No References.

MOVING_CA¶

BC = MOVING_CA NS <bc_id> <float_list>

Description / Usage¶

(PCC/ROTATED MOMENTUM)

The intent of this boundary condition is to apply a contact angle at wetting in a twodimensional flow that is a function of the rate of advance or recession of the contact line over the substrate. It is experimental, untested, and unsupported; use it at your own risk.

There are ten values that must be specified in the <float_list>; definitions of the input parameters are as follows:

MOVING_CA	Name of the boundary condition.
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain. A KINEMATIC free surface must terminate at this single-node node set.
<float1>	\(\theta_{stc}\), the static contact angle, in degrees.
<float2>	\(n_x\), the x-component of solid surface normal vector.
<float3>	\(n_y\), the y-component of solid surface normal vector.
<float4>	\(n_z\), the z-component of solid surface normal vector.
<float5>	\(\theta_{adv}\), the advancing contact angle, in degrees.
<float6>	\(\theta_{rec}\), the receding contact angle, in degrees.
<float7>	\(\alpha\), the scale-factor, see below.
<float8>	\(v_{wx}\), the x-component of wall velocity.
<float9>	\(v_{wy}\), the y-component of wall velocity.
<float10>	\(v_{wz}\), the z-component of wall velocity.

Examples¶

The following is a sample input card:

BC = MOVING_CA NS 100 90.0 0. 1. 0. 135.0 45.0 1.0 -1. 0. 0.

Technical Discussion¶

This boundary condition applies a point collocated constraint on the angle between the solid surface vector and the free-surface normal of the form:

where n is the solid surface vector specified on the card and \(n_{fs}\) is the free-surface normal computed automatically by Goma. The contact angle is variable depending upon the relative velocity of the mesh speed, \(\dot{x}\) , and the substrate speed, \(v_w\) specified on the card float_list:

This constraint on the moving contact angle replaces a rotated component of the momentum equation. In effect a wetting force is applied at the contact line whose magnitude depends on the discrepancy between actual contact angle and that computed by the above expressions. Note that other contact angle constraints are applied to rotated components of the mesh equation. A real question exists whether such a formulation is consistent with a KINEMATIC boundary condition also applied to this node.
Not also that since this boundary condition is applied to the momentum equation, care must be taken to relax any Dirichlet on the substrate velocity. Otherwise, this latter constraint will override this constraint.
Users are again cautioned that this boundary condition is untested and potentially inconsistent. It may not work.

SDC_STEFANFLOW¶

BC = SDC_STEFANFLOW SS <bc_id> <integer> {char_string}

Description / Usage¶

(SIC/MOMENTUM)

This boundary condition represents the specification of the normal component of the interfacial velocity on one side of the interface. These are DVI_SIDTIE_VD boundary conditions (Moffat, 2001) that have an additional property. The first time encountered in the formation of the residual, the results of a sub calculation are stored either at the node structure level or at the surface Gauss point level. The surface reaction and surface species are specified as part of a surface domain within Chemkin.

The SURFDOMAINCHEMKIN_STEFAN_FLOW (shortened to SDC_STEFANFLOW in the name2 member of the BC_descriptions struct in mm_names.h) boundary condition solves the following equation representing Stefan flow at a boundary.

where \(n_l\) is the outward facing normal to the liquid material, \(p^l\) is the liquid density, \(u^l\) is the (mass average) velocity at the current surface quadrature point, and \(u_s\) the velocity of the mesh (i.e., the interface if the mesh is fixed at the interface). The summation over N species is for the product of molecular weight ( \(W_k\) ) and the source term for creation of species k in the liquid ( \(S_k^l\) ). Note, while it may seem that one side of the interface is getting special treatment, the combination of this boundary condition with the KINEMATIC_CHEM boundary condition actually creates a symmetric treatment of the boundary condition. SDC_STEFANFLOW is linked to the SDC_SPECIES_RXN boundary conditions just as the KINEMATIC_CHEM boundary conditions are by the expression for the interface reaction. The sum is over all of the interfacial source terms for species in the phase.

Definitions of the input parameters are as follows:

SDC_STEFANFLOW	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer>	Element Block ID of the phase on whose side of the interface this boundary condition will be applied.
char_string	\(S_k^l\), string indicating where the surface source term information for this boundary condition will be obtained. Three options exist: IS_EQUIL_PSEUDORXN VL_EQUIL_PSEUDORXN SDC_SURFRXN These are boundary conditions that apply to the Species Equations. The last boundary condition is not yet implemented, so SDC_SURFRXN currently does nothing.

Examples¶

The following is a sample input card:

BC = SDC_STEFANFLOW SS 1   0 VL_EQUIL_PSEUDORXN

The above card will create a strongly integrated boundary condition specifying the normal component of the velocity on side set 1 on the element block 0 side of the interface. The source term to be used will be taken from multiple previously specified VL_EQUIL_PSEUDORXN cards.

Technical Discussion¶

Currently, this card has only been tested on internal interfaces containing discontinuous interfaces using the VL_EQUIL_PSEUDORXN source term. The SDC_SURFRXN boundary condition has not been implemented yet.
The DVI_SIDTIE_VD variable is a nomenclature adopted by Moffat (2001) in his development of a revised discontinuous variable implementation for Goma. It pertains to Discontinuous Variable Interfaces (DVI) and the strongly integrated Dirichlet (SID) boundary conditions prescribing the discontinuous value of variables on either side of an interface (TIE boundary conditions). The user is referred to Moffat (2001) for detailed presentation on discontinuous variables.

References¶

GTM-015.1: Implementation Plan for Upgrading Boundary Conditions at Discontinuous-Variable Interfaces, January 8, 2001, H. K. Moffat

FLUID_SOLID¶

BC = FLUID_SOLID SS <bc_id> <integer1> <integer2> [float]

Description / Usage¶

(PCC/VECTOR MOMENTUM)

Used for fluid-structure interaction problems, the FLUID_SOLID condition equates the normal traction (the tangential and normal force components, per unit area) between adjacent fluid and solid materials. This condition is only to be used on boundaries between regions of ARBITRARY mesh motion with fluid momentum equations and of LAGRANGIAN or DYNAMIC_LAGRANGIAN mesh motion, with solid momentum equations (or mesh equations); see Mesh Motion and EQ cards. With this boundary condition, the local residual and Jacobian contributions from the fluid mechanics momentum equations (on the ARBITRARY side of the boundary) are added into weak form of the residual and Jacobian entries for the solid mechanics equations (on the solid LAGRANGIAN side of the boundary). All elements on both sides of the interface must have the same element type, i.e., the same order of interpolation and basis functions, e.g., Q1 or Q2. Also, such interfaces must include element sides from both sides of the interface in the defining side set.

Definitions of the input parameters are as follows:

FLUID_SOLID	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer1>	Element block ID of solid phase (of LAGRANGIAN motion type) from the EXODUS II database.
<integer2>	Element block ID of liquid phase from the EXODUS II database.
[float]	Scale factor for stress balance for non-dimensionalization. This parameter, which multiplies the solid phase contribution, is optional; the default is 1.0.

Examples¶

The following is a sample input card:

BC = FLUID_SOLID SS 5   2   1

In this example, side set 5 is a boundary between a solid blade and a liquid; material 2 is the rubber blade, and material 1 is the fluid. Along that blade, a companion boundary condition of the form

BC = NO_SLIP SS 5   2 1

should also be applied.

Technical Discussion¶

The functional form of the boundary condition is:

where \(\underline{T}\) is the fluid phase stress tensor given by any one of the specified fluid-phase constitutive equations, \(\underline{\sigma}\) and is the solid-phase stress tensor, also given by any one of the solid-phase constitutive equation (see material file specifications). \(\lambda\) is a scaling factor that defaults to unity (and is usually best taken as such unless some scaling is invoked).

This balance is applied to the weak form of the solid-phase momentum residuals, from the fluid phase, viz. in the fluid-phase, the fluid-stress at the interface is added to the solid-phase momentum residuals. As mentioned above, this condition usually needs to be supplemented by a statement of mass conservation across the interface, which will depend on whether the solid phase is of CONTINUOUS or POROUS media (see Media Type card).

FAQs¶

Troubleshooting 1: This boundary condition requires that the side set contain elements from both the fluid and the solid side of the interface. For the FASTQ tool, this is the default case; for CUBIT and possibly other related tools, this can be forced on the side set definition options. Interestingly, the boundary condition does work if the side set is attached to the fluid phase only, but just due to the way in which it is applied.

Troubleshooting 2: This boundary condition does not enforce mass conservation. A combination of NO_SLIP or VELO_NORMAL/VELO_TANGENT must be invoked to achieve a material surface. For the latter, care must be taken to maintain the application of the VELO_NORMAL condition after a remesh. This condition is applied only to one side of the interface and depends on the ss_to_blks connectivity structure; it may be necessary to force its application, especially after remeshes. To be sure that the proper set of conditions is being applied, look at the BC_dup.txt file for nodes along the interface.

References¶

GT-003.1: Roll coating templates and tutorial for GOMA and SEAMS, February 29, 2000, P. R. Schunk and Matt Stay

GT-006.3: Slot and Roll coating with remeshing templates and tutorial for GOMA and CUBIT/MAPVAR, August 3, 1999, R. R. Lober and P. R. Schunk

FLUID_SOLID_RS¶

BC = FLUID_SOLID_RS SS <bc_id> <integer1> <integer2> [float]

Description / Usage¶

(WIC/VECTOR MOMENTUM)

Please see SOLID_FLUID_RS. This boundary condition has not yet been implemented.

Examples¶

No Examples.

Technical Discussion¶

No Discussion.

References¶

No References.

DARCY_CONTINUOUS¶

BC = DARCY_CONTINOUS SS <bc_id> <integer1> <integer2> [float1]

Description / Usage¶

(SIC/ROTATED MOMENTUM)

This condition enforces continuity of mass flux at an interface between a continuous medium and a saturated or partially saturated porous medium. In other words, DARCY_CONTINUOUS is a boundary condition that equates the velocity component in the liquid phase normal to the interface with the Darcy velocity in the porous phase, normal to the same interface, with proper accounting for conservation of mass using the liquid phase densities in the material files.

DARCY_CONTINOUS	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer1>	Element block ID of porous phase from the EXODUS II database.
<integer2>	Element block ID of continuous fluid phase from the EXODUS II database.
[float1]	An optional floating point that is used for level-set free surface problems. This floating point represents a length scale over which “contact” of a liquid free surface represented by a level set field and a porous medium. It should be set to some small integer multiple of the smallest element size along the boundary. Note that this length scale is only required in cases where “sharp” interfaces using subelement integration are used. It is not required for diffuse interface representations.

Examples¶

The boundary condition

BC = DARCY_CONTINUOUS SS 5 2 1

applies to the interface defined by side set 5 which joins EXODUS II block 2 (porous phase) and block 1 (continuous phase).

Technical Discussion¶

The DARCY_CONTINUOUS boundary condition imposes the following requirement at the interface between a continuous medium and a saturated or partially saturated porous medium:

where \(\underline{n}\) is the outward-pointing normal to the surface, \(\underline{q}\) is the Darcy flux, \(p_l\) is the liquid density, presumed to be the same in the adjacent phases, \(\underline{v}\) is the fluid velocity and \(\underline{v}_s\) is the mesh velocity.

Typically this boundary condition is applied between two blocks, one being of a LAGRANGIAN mesh motion type (see Mesh Motion card) and the other being of an ARBITRARY mesh motion type. Within the LAGRANGIAN material the Media Type card is set to POROUS_SATURATED, POROUS_UNSATURATED, or POROUS_TWO_PHASE. The other block is of type CONTINOUS.

Refer to the citations below where this boundary condition is discussed in more detail.

FAQs¶

Important troubleshooting note: Density, as specified in the material files for the continuous and porous phase, MUST be the same for this boundary condition to make sense.

References¶

GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk

GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk

GT-028.0: Liquid Drop Impact on a Porous Substrate: a level-set tutorial, August 15, 2005.

VN_POROUS¶

BC = VN_POROUS SS <bc_id> <integer_list> <float>

Description / Usage¶

(SIC/ROTATED MOMENTUM)

This boundary condition is used to calculate the normal component of gas phase velocity at the interface between a continuous gas phase and porous phase. The condition is basically the unsaturated equivalent to DARCY_CONTINUOUS, and hence is a condition on the normal component of fluid (gas) velocity on the continuous side of the interface (see below). The flux on the porous medium side includes Darcy flux and Fickian diffusive flux in the porous phase. The vapor flux into gas is used to determine gas velocity. The condition is similar to the solid-liquid interface conditions that apply to interfaces between a porous medium and an external gas (in which the energy equation is used to solve for solvent concentration in the gas phase). This boundary condition is still under development and has not been recently tested. Its last use was for evaporation from a porous unsaturated film in a sol-gel application (see references below).

There are three values to be supplied for the <integer_list>; definitions of the input parameters are as follows:

VN_POROUS	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer1>	Element block ID of solid, porous phase from the EXODUS II database.
<integer2>	Element block ID of gas phase from the EXODUS II database.
<integer3>	Set to zero for now, indicating that this condition pertains to the primary liquid solvent vapor. At some point this will be generalized to include all vapor components.
<float>	Density of pure solvent vapor.

Examples¶

The following is a sample input card:

BC = VN_POROUS SS 5   1 2 0 1.e-3

This condition applies to internal side set 5, which defines the interface between element block 1 (the solid porous phase which has Media Type of POROUS_PART_SAT or POROUS_TWO_PHASE) and element block 2 (the fluid phase which has Media Type CONTINUOUS). It is based on the flux of liquid solvent in the porous phase (denoted by the integer 0), the vapor form of which has a density of 1.e-3. The condition results in a blowing or sucking velocity at the interface in the fluid (gas) continuous phase.

Technical Discussion¶

The functional form of this boundary condition is

Here, the left hand side is the total flux of liquid solvent, in both gas and liquid phases. The first two terms are the Darcy pressure driven contributions, and the second two terms are the Fickian flux contributions.

This condition would be useful for predicting the gas-flow pattern above a drying porous matrix, in which the vapor flux being driven out of the porous skeleton were a mass source to drive flow in the surrounding gas. The condition has not been tested since 1995.

References¶

GTM-028.0: Modeling Drying of Dip-Coated Films with Strongly-Coupled Gas Phase Natural Convection, R. A. Cairncross, 1999.

CAPILLARY_SHEAR_VISC¶

BC = CAPILLARY_SHEAR_VISC SS <bc_id> <float_list> [integer]

Description / Usage¶

(WIC/VECTOR MOMENTUM)

This boundary condition card is used to apply additional capillary forces beyond surface tension and surface tension gradients (as applied with use of the CAPILLARY BC) to the momentum equation on a free-surface. These additional forces are caused by surface deformation (surface expansion/contraction/shear) in the presence of surface-active species. Microstructural layers of surfactants in a capillary free surface can lead to significant dissipation of mechanical energy due to an effective surface viscosity. These additional properties are specified as inputs to this boundary condition.

Definitions of the input parameters are as follows:

CAPILLARY_SHEAR_VISC	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	\(\mu_s\), surface shear viscosity.
<float2>	\(\kappa_s\) , surface extensional/dilatational viscosity.
[integer]	Optional integer value indicating the element block id from which to apply the boundary condition. This is used to force the capillary stresses to be applied from within a phase where the momentum equations are defined.

Examples¶

Following is a sample card:

BC = CAPILLARY SS 12   1.0 10.0 0.0

BC = CAPILLARY_SHEAR_VISC SS 12   0.001 0.01

These cards specifies that capillary forces be applied to the free surface on side set 12. If a surface tension material parameter value or model is supplied, this is the surface tension value used. If not, the surface tension value used is 1.0. An external isotropic pressure of 10.0 is applied from the surrounding environment. The second card adds a surface viscosity effect. Note that you must solve the shell equation EQ = n_dot_curl_v to pick up this term.

Technical Discussion¶

The functional form of this boundary condition is

where n is the outward normal to the surface, T is the fluid stress tensor, \(\P_{ex}\) is the external applied pressure described above, H is the surface curvature defined as, H = – \(\Delta_s\) ⋅ n ⁄ 2, \(\sigma\) is the surface tension, and \(\Delta_s\) is the surface divergence operator defined as \(\Delta_s\) f = (I – nn) ⋅ \(\Delta\) f .

The Boussinesq-Scriven surface rheological constitutive equation is as follows:

Here, \(\Delta_s\) = ( \(\underline{I}\) – \(\underline{nn}\) ) ⋅ \(\Delta\) is the surface gradient operator, \(I_s\) = (\(\underline{I}\) - (\(\underline{nn}\) ) unit tensor. \(\mu_s\) and \(\kappa_s\) is the surface are the surface shear viscosity and surface dilatational viscosity, respectively. The terms beyond the first three on the right are added by this boundary condition card. Note that the first three terms on the right are balance of the stress in the standard goma CAPILLARY condition, with surface tension gradients being accommodated through variable surface tension. The boundary condition CAPILLARY_SHEAR_VISC is used to set the additional terms of this constitutive equation. As of January 2006 only the 7th term on the right hand side is implemented, as it is the only nonzero term in a flat surface shear viscometer. The building blocks for the other terms are available through additional shell equations (specifically you must solve EQ = n_dot_curl_v equation on the same shell surface). . These remaining terms actually represent additional dissipation caused by surface active species microstructures flowing in the surface. The best source of discussion of this equation is a book by Edwards et al. (1991. Interfacial Transport Processes and Rheology. Butterworth-Heinemann, Boston).

VELO_THETA_COX¶

BC = VELO_THETA_COX NS <bc_id> <float_list> [integer]

Description / Usage¶

(PCC/R_MOM_TANG1)

This boundary condition card applies a dynamic contact angle dependent velocity condition in a similiar fashion to VELO_THETA_TPL, but the functional form of the velocity is different. The functional form stems from the hydrodynamic theory of wetting by Cox.

The <float_list> for this boundary condition has eight values; definitions of the input parameters are as follows:

VELO_THETA_COX	Name of the boundary condition.
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	\(\theta\), equilibrium (static) contact angle subtended by wall normal and free surface normal, in units of degrees.
<float2>	\(n_x\) , x-component of normal vector to the geometry boundary (see important note below regarding variable wall normals, viz. non-planar solid walls).
<float3>	\(n_y\) , y-component of normal vector to the geometry boundary. (see important note below regarding variable wall normals, viz. non-planar solid walls).
<float4>	\(n_z\) , z-component of normal vector to the geometry boundary. (see important note below regarding variable wall normals, viz. non-planar solid walls).
<float5>	\(\varepsilon_s\) is the dimensionless slip length, i.e. the ratio of the slip length to the characteristic length scale of the macroscopic flow.
<float6>	\(\sigma\) is the surface tension. This value is multiplied by the surface tension value stipulated by the surface tension material model.
<float7>	\(t_{relax}\) is a relaxation time which can be used to smooth the imposed contact point velocity for transient problems. Set to zero for no smoothing.
<float8>	\(V_{old}\) is an initial velocity used in velocity smoothing for transient problems. Set to zero when smoothing is not used.
[integer]	blk_id, an optional parameter that is the element block number in conjugate problems that identifies the material region to which the contact angle applies (usually the liquid element block in solid/liquid conjugate problems).

Examples¶

Following is a sample card:

BC = VELO_THETA_COX NS   100   {45}   0.   1.   0. 0.1   72.0   0   0   2

This condition applies a contact angle of 45 degrees between the free surface normal at the 100 nodeset and the vector (0,1,0). The surface tension is 72, the reciprocal of the slip coefficient is 0.1, and the dynamic contact angle is taken from element block 2. Normally, this latter vector is the normal to the solid surface in contact with the free surface at this point.

Technical Discussion¶

The constraint that is imposed at the nodeset node is as follows:

where \(v_{Cox}\) is computed from

where the Cox functions, f and g, are given by;

The parameters \(\lambda\), \(q_{inner}\), and \(q_{outer}\) are currently not accessible from the input card and are hard-set to zero. \(\lambda\) is the ratio of gas viscosity to liquid viscosity whereas \(q_{inner}\) and \(q_{outer}\) represent influences from the inner and outer flow regions

When smoothing is not used, i.e. \(t_{relax}\) = 0 , the imposed velocity is equal to that stipulated by the Hoffman correlation. Also see WETTING_SPEED_COX and SHARP_COX_VELOCITY for level-set versions.

For steady problems, the substrate velocity will be extracted from adjoining VELO_TANGENT, VELO_SLIP, or VELO_SLIP_ROT boundary conditions.
The Cox wetting velocity requires evaluation of integrals for the function g ( \(\theta\), \(\lambda\)) which is currently done numerically using 10-point Gaussian quadrature. As such the evaluation of the integrals is expected to become inaccurate as either \(\theta_eq\) tends toward zero or \(\theta\) tends toward 180 degrees. Note that the integrand becomes singular as \(\theta\) tends toward 0 or 180 degrees.
This condition was motivated by the Cox hydrodynamic theory of wetting (cf. Stephan F. Kistler, “Hydrodynamics of Wetting,” in Wettability edited by John Berg, 1993 ).

VELO_THETA_HOFFMAN¶

BC = VELO_THETA_HOFFMAN NS <bc_id> <float_list> [integer]

Description / Usage¶

(PCC/R_MOM_TANG1)

This boundary condition card applies a dynamic contact angle dependent velocity condition in a similiar fashion to VELO_THETA_TPL, but the functional form of the velocity is different. The functional form stems not from a theory of wetting, but instead, from a correlation of many empirical measurements.

The <float_list> for this boundary condition has eight values; definitions of the input parameters are as follows:

VELO_THETA_HOFFMAN	Name of the boundary condition.
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	\(\theta\), equilibrium (static) contact angle subtended by wall normal and free surface normal, in units of degrees.
<float2>	\(n_x\) , x-component of normal vector to the geometry boundary (see important note below regarding variable wall normals, viz. non-planar solid walls).
<float3>	\(n_y\) , y-component of normal vector to the geometry boundary. (see important note below regarding variable wall normals, viz. non-planar solid walls).
<float4>	\(n_z\) , z-component of normal vector to the geometry boundary. (see important note below regarding variable wall normals, viz. non-planar solid walls).
<float5>	currently not used.
<float6>	\(\sigma\) is the surface tension. This value is multiplied by the surface tension value stipulated by the surface tension material model.
<float7>	\(t_{relax}\) is a relaxation time which can be used to smooth the imposed contact point velocity for transient problems. Set to zero for no smoothing.
<float8>	\(V_{old}\) is an initial velocity used in velocity smoothing for transient problems. Set to zero when smoothing is not used.
[integer]	blk_id, an optional parameter that is the element block number in conjugate problems that identifies the material region to which the contact angle applies (usually the liquid element block in solid/liquid conjugate problems).

Examples¶

Following is a sample card:

BC = VELO_THETA_HOFFMAN NS   100   {45}   0.   1.   0.   0.   72.0   0   0   2

This condition applies a contact angle of 45 degrees between the free surface normal at the 100 nodeset and the vector (0,1,0). The surface tension is 72 and the dynamic contact angle is taken from element block 2. Normally, this latter vector is the normal to the solid surface in contact with the free surface at this point.

Technical Discussion¶

The constraint that is imposed at the nodeset node is as follows:

where \(v_{Hoffman}\) is computed from the implicit solution of the Hoffman correlation;

or

where the Hoffman functions, fHoff and gHoff, which are inverses of each other are given by;

When smoothing is not used, i.e. \(t_{relax}\) = 0 , the imposed velocity is equal to that stipulated by the Hoffman correlation. Also see WETTING_SPEED_HOFFMAN and SHARP_HOFFMAN_VELOCITY for level-set versions.

For steady problems, the substrate velocity will be extracted from adjoining VELO_TANGENT, VELO_SLIP, or VELO_SLIP_ROT boundary conditions.
Because the Hoffman functions are implicit, iteration is required in the determination of the wetting velocity. As a result, for very high capillary numbers, i.e. > \(10^6\), the iteration procedure in Goma may need to be modified.
This condition was motivated by the Hoffman empirical correlation (cf. Stephan F. Kistler, “Hydrodynamics of Wetting,” in Wettability edited by John Berg, 1993).

VELO_THETA_TPL¶

BC = VELO_THETA_TPL NS <bc_id> <float_list> [integer]

Description / Usage¶

(PCC/R_MOM_TANG1)

This boundary condition card applies a dynamic contact angle dependent velocity condition in place of one component of the fluid momentum equation (unlike CA_BC which applies a fixed contact angle condition ot the mesh equation). The functional form of this condition is given below and stems from the Blake-DeConinck psuedomolecular kinetics theory of wetting. It is recommended that this condition or other forms of it (cf. VELO_THETA_HOFFMAN or VELO_THETA_COX) be used for steady and transient ALE problems. If you are deploying level-set technology to track moving capillary surfaces and three-phase wetting lines then the counterpart to this condition is WETTING_SPEED_LINEAR. It is noteworthy that this condition is applied to the fluid momentum equation, so that the velocity of the wetting line and the cosine of the current measured contact angle difference with the specified static value are related in a linear way.

The <float_list> for this boundary condition has eight values; definitions of the input parameters are as follows:

VELO_THETA_TPL	Name of the boundary condition.
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	\(\theta\), equilibrium (static) contact angle subtended by wall normal and free surface normal, in units of degrees.
<float2>	\(n_x\) , x-component of normal vector to the geometry boundary (see important note below regarding variable wall normals, viz. non-planar solid walls).
<float3>	\(n_y\) , y-component of normal vector to the geometry boundary. (see important note below regarding variable wall normals, viz. non-planar solid walls).
<float4>	\(n_z\) , z-component of normal vector to the geometry boundary. (see important note below regarding variable wall normals, viz. non-planar solid walls).
<float5>	V_0 is a pre-exponential velocity factor (see functional form below)
<float6>	g is a thermally scaled surface tension, i.e. \(\sigma\) /2nkT. This value is multiplied by the surface tension value stipulated by the surface tension material model.
<float7>	\(t_{relax}\) is a relaxation time which can be used to smooth the imposed contact point velocity for transient problems. Set to zero for no smoothing.
<float8>	\(V_{old}\) is an initial velocity used in velocity smoothing for transient problems. Set to zero when smoothing is not used.
[integer]	blk_id, an optional parameter that is the element block number in conjugate problems that identifies the material region to which the contact angle applies (usually the liquid element block in solid/liquid conjugate problems). NOTE/ WARNING: As of 1/13/2013 this option seems not to work with TALE problems.

Examples¶

Following is a sample card:

BC = VELO_THETA_TPL NS   100   {45}   0.   1.  0.  1000.0   5.e-4   0   0

This condition applies a contact angle of 45 degrees between the free surface normal at the 100 nodeset and the vector (0,1,0). The velocity scale is 1000 and the sensitivity scale is 5.e-4. Normally, this latter vector is the normal to the solid surface in contact with the free surface at this point.

Technical Discussion¶

The constraint that is imposed at the nodeset node is as follows:

When smoothing is not used, i.e. \(t_{relax}\) = 0 , the imposed velocity is equal to that stipulated by the Blake-DeConinck equation. Also see WETTING_SPEED_LINEAR and WETTING_SPEED_BLAKE for level-set versions of this and VELO_THETA_HOFFMAN and VELO_THETA_COX for other functional forms.

We recommend use of this condition over CA_BC for all transient problems. In this case this condition displaces a momentum equation component, with the other component being used to enforce no substrate penetration. The kinematic condition is applied to the mesh motion a this node so as to conserve mass.
For steady problems, the substrate velocity will be extracted from adjoining VELO_TANGENT, VELO_SLIP, or VELO_SLIP_ROT boundary conditions.
Important: Variable Wall Normals. Situations for which the wall shape is nonplanar, meaning that the normal vector is not invariant as the contact line moves, there is an option to leave all of the normal-vector components zero. In this case Goma then seeks to determine the local wall normal vector from the geometry it is currently on, using the element facets. It is recommended that this option not be used unless the geometry is truly nonplanar, as the logic is complex and not 100% reliable. See documentation for CA_BC for an example.
This condition was motivated by T. D. Blake and is the so-called Blake- DeConinck condition (T. D. Blake, J. De Coninck 2002. “The influence of solidliquid interactions on dynamic wetting”, Advances in Colloid and Interface Science 96, 21-36. ). See this article for some options for the form of the preexponential velocity, V_0.
Important: Wall Normal convention. The wall normal vector on an external solid boundary is defined in goma as the inward facing normal to the mesh, and the free surface normal to the liquid (or wetting phase for two-liquid systems) is defined as the outward facing normal to the free surface. Put another way and referring to the picture below, the wall normal is directed from the “solid phase” to the “liquid phase”, and the free surface normal is directed from the “liquid phase” or “wetting phase” to the “vapor phase” or “Non-wetting phase”. Note that for zero contact angle the liquid is “perfectly wetting”. The air-entrainment limit (viz. the hydrodynamic theory interpretation) would occure at a 180 degree contact angle. Recall that the angle is specified in radians on this card.

SHEET_ENDSLOPE¶

BC = SHEET_ENDSLOPE NS <bc_id> <float_list>

Description / Usage¶

(SPECIAL/VECTOR MOMENTUM)

This boundary condition card is used to enforce a slope of a membrane surface (cf. to be used in conjuction with BC = TENSION_SHEET) at its enpoints. . There are two values to be input for the <float_list>; definitions of the input parameters are as follows:

SHEET_ENDFORCE	Name of the boundary condition (<bc_name>).
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	X-component of upstream idler point (see discussion below)
<float2>	Y-component of upstream idler point.

Examples¶

The following is a sample input card using several APREPRO variables:

BC = SHEET_ENDSLOPE NS 100   {sind(th2)}   {-cosd(th2)

This condition would enforce a slope equivalent to that defined between the coordinates of the node at NS 100 with the point [sind(th2), -cosd(th2)].

Technical Discussion¶

Only two dimensional applications, viz. the nodeset is a single-node nodeset.

This is a single point nodeset boundary condition. Its function is to set the slope of the web at the single point nodeset N. It does this by enforcing continuity of the slope of the TENSION_SHEET sideset with the straight line that connects the point (X,Y) with nodeset N. Thus, this boundary condition can be used to model the influence of an upstream idler roller located at the point (X,Y). Indeed, this boundary condition has an alternate name: IDLER_LOC.

This boundary condition exploits the natural boundary conditions associated with the TENSION_SHEET formulation so it really can only beused in conjunction with the latter boundary condition.

One caveat that must be mentioned is that the formulation of these two boundary conditions is not general and therefore they should only be applied to web geometries that are predominantly horizontal. That is, the x component of the normal vector to the web sideset should at each point be less than or equal to the y component.

TENSION_SHEET¶

BC = TENSION_SHEET SS <bc_id> <float>

Description / Usage¶

(SIC/VECTOR MOMENTUM)

This boundary condition card is used to apply a membrane force to the fluid momentum equation in order to model a membrane-like structure, viz. one with no bending stiffness but with significant tension much larger than the fluid viscous stresses. This boundary condition is basically the same mathematically as the capillary condition, with the tension here specified instead of a capillary surface tension. The only difference is the way in which it is applied: it is applied as a strong integrated condition instead of a weak form condition.

Definitions of the input parameters are as follows:

TENSION_SHEET	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	Τ, Tension of the membrane.

Examples¶

Following is a sample card:

BC = TENSION_SHEET SS 12

Technical Discussion¶

Usage notes:

Can only be applied in two dimensions.
One caveat that must be mentioned is that the formulation of these two boundary conditions is not general and therefore they should only be applied to web geometries that are predominantly horizontal. That is, the x component of the normal vector to the web sideset should at each point be less than or equal to the y component.
To set the slope of the membrane at an endpoint, see the BC = SHEET_ENDSLOPE card.
This boundary condition that can be used to model the interaction of fluid with a thin sheet under a constant tension load. The sideset to which it is applied must be fully “wetted” by a fluid. Note that this boundary condition arises as a simplification of the tensioned-web shell equations (cf. shell_tension and shell_curvature equations as described in GT-033.0 and GT-027.0) subject to two simplifying assumptions:
1. The sheet supports no bending moments. That is, it isn’t very rigid.
2. The tension in the sheet is significantly larger than the viscous stresses in the fluid.

Given these assumptions this boundary condition can be used to model tensioned web applications without having to resort to the shell equations. It is a strongly integrated, rotated boundary condition on the mesh equations. It can only be used in twodimensional applications.

References¶

GT-033.0 and GT-027.0.

Category 5: Energy Equations¶

The following conditions are applied as boundary conditions to the energy equation. These conditions include strong Dirichlet conditions, such as hard sets on temperature on a boundary as a constant or function of position, weak-form conditions, such as a specified heat flux from a convective heat transfer model or a constant flux, and a host of interfacial conditions for phase change (viz. latent heat effects), etc. The energy equation is of course a scalar equation. Some with a molten metal surface. These conditions will also apply in general to the porous energy equation (see Porous Energy). highly specialized equations are also available, such as a heat flux model for a laser interaction

T¶

BC = T NS <bc_id> <float1> [float2]

Description / Usage¶

(DC/ENERGY)

This Dirichlet boundary condition card is used to set constant temperature. Definitions of the input parameters are as follows:

T	Name of the boundary condition (<bc_name>).
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	Value of temperature.
[float2]	An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

The following is a sample input card:

BC = T NS 100 273.13

Technical Discussion¶

No Discussion.

T_USER¶

BC = T_USER SS <bc_id> <float_list>

Description / Usage¶

(PCC/ENERGY)

This boundary condition card is used to call a routine for a user-defined temperature. Specification is made via the function tuser in file “user_bc.c.” Definitions of the input parameters are as follows:

T_USER	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float_list>	A list of float values separated by spaces which will be passed to the user-defined subroutine so the user can vary the parameters of the boundary condition. This list of float values is passed as a one-dimensional double array to the appropriate C function in file user_bc.c.

Examples¶

The following is a sample input card with two parameters passed to function tuser:

BC = T_USER SS 100   273.13 100.0

Technical Discussion¶

No Discussion.

References¶

No References.

QCONV¶

BC = QCONV SS <bc_id> <float1> <float2>

Description / Usage¶

(WIC/ENERGY)

This boundary condition card specifies convective heat flux. Definitions of the input parameters are as follows:

QCONV	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	h, heat transfer coefficient.
<float2>	\(T_s\), sink temperature.

Examples¶

The following is a sample card:

BC = QCONV SS 100 10.0 293.0

Technical Discussion¶

The convective heat flux is defined as

where h and \(T_s\) are the convective heat transfer coefficient and the sink temperature, respectively.

QRAD¶

BC = QRAD SS <bc_id> <float_list>

Description / Usage¶

(WIC/ENERGY)

This boundary condition card specifies heat flux using both convective and radiative terms. The <float_list> has four parameters; definitions of the input parameters are as follows:

QRAD	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	h, convective heat transfer coefficient.
<float2>	\(T_s\), sink temperature.
<float3>	\(\varepsilon\), total hemispherical emissivity.
<float4>	\(\sigma\), Stefan-Boltzmann constant.

Examples¶

The following is a sample card:

BC = QRAD SS 100 10.0 273.0 0.3 5.6697e-8

Technical Discussion¶

The heat flux definition for this card is a combined convective and radiative formulation:

where h and \(T_s\) are the convective heat transfer coefficient and the sink temperature, and \(\varepsilon\) and \(\sigma\) are the total hemispherical emissivity and Stefan-Boltzmann constant, respectively. The latter constant has been made an input parameter rather than a code constant so that the user can specify its value in units that are consistent for the problem being modeled.

The QRAD boundary condition can be used in place of QCONV by simply setting the emissivity value to zero.

QSIDE¶

BC = QSIDE SS <bc_id> <float1>

Description / Usage¶

(WIC/ENERGY)

This boundary condition card is used to specify a constant heat flux. Definitions of the input parameters are as follows:

QSIDE	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	Value of heat flux. A positive value implies that energy is being added to system; a negative value implies energy is being taken from the system through the boundary.

Examples¶

The following is a sample card:

BC = QSIDE SS 22   1.50

Technical Discussion¶

The mathematical form of the boundary condition.

T_CONTACT_RESIS, T_CONTACT_RESIS_2¶

BC = T_CONTACT_RESIS SS <bc_id> <int1> <int2> <float1>

BC = T_CONTACT_RESIS_2 SS <bc_id> <int2> <int1> <float1>

Description / Usage¶

(WIC/ENERGY)

This boundary condition set is used to specify a thermal contact resistance at an interface between two mesh regions defined by a side set. Please see special usage notes below regarding proper side-set specification and the reasons that both BC cards are required for an internal interface. NOTE that the temperature field MUST be interpolated with the discontinous versions of Q1 or Q2, viz. Q1_D and Q2_D. Definitions of the input parameters are as follows:

T_CONTACT_RESIS	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database. Note this side set MUST contain elements on both sides of the interface.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<int1>	Material/region ID associated with first material.
<int2>	Material/region ID associated with second material. Note that these material IDs are reversed on the second BC.
<float1>	Value contact resistance in units of thermal conductivity divided by length.

Examples¶

The following is a sample card:

BC = T_CONTACT_RESIS SS 3 1 2 10.0

BC = T_CONTACT_RESIS_2 SS 3 2 1 10.0

Note that both boundary condition cards are required at an internal interface. In this case the interface divides mesh/material ID 1 and 2. Note also how these material IDs are reversed on the second card. These conditions apply a thermal contact resistance of 10. (units of thermal conductivity divided by length) at the interface defined by SS 3.

Technical Discussion¶

The mathematical form of the boundary condition.

The flux into the interface from material “a” is equivalent to that into material “b”, both equal to the temperature jump across the interface times the contact resistance \(R^{-1}\).

The side set to which this boundary condition is applied must contain elements on both sides of the interface. Look up any special commands in your mesh generator to make sure this occurs. In CUBIT, for example, you have to add “wrt volume 1 2” like qualifiers on the side set command. The reason for the “double application” of this condition is to pick up the all the terms from both sides of the interface with the proper sign. The nodes at the interface have two temperatures, one from each side, and so two weak form applications of this equation are required, one from each side.

QNOBC¶

BC = QNOBC SS <bc_id>

Description / Usage¶

(WIC/ENERGY)

This boundary condition card applies the open boundary condition equivalent on the energy equation (see momentum open BC FLOW_STRESSNOBC)

QNOBC	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.

Examples¶

Following is a sample card:

BC = QNOBC SS 3

Here the BC is applied to SS 3

Technical Discussion¶

The finite element formulation of the energy equation generates boundary integrals of the form:

\[\int_\Gamma \mathbf{n} \cdot \mathbf{q}\ dS\]

where \(\mathbf{q}\) is the heat flux.

This boundary condition adds this term back in at the boundary avoiding the natural boundary condition.

References¶

Griffiths, D.F., “The ‘no boundary condition’ outflow boundary condition,” IJNMF, 24, 393-411, (1997)

Sani, R.L., and P.M. Gresho, “Resume and remarks on the open boundary condition minisymposium,” IJNMF, 18, 983-1008, (1994).

QUSER¶

BC = QUSER SS <bc_id> <float_list>

Description / Usage¶

(WIC/ENERGY)

This boundary condition card is used to call a routine for a user-defined heat flux model. Definitions of the input parameters are as follows:

QUSER	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float_list>	A list of float values separated by spaces which will be passed to the user-defined subroutines so the user can vary the parameters of the boundary condition. This list of float values is passed as a one-dimensional double array to the quser_surf C function in file user_bc.c.

Examples¶

The following is a sample input card for a heat flux model requiring two parameters:

BC = QUSER SS 100   10.0 3.14159

Technical Discussion¶

No Discussion.

Q_VELO_SLIP¶

BC = Q_VELO_SLIP SS <bc_id>

Description / Usage¶

(WIC/ENERGY)

This boundary condition card is used to calculate the surface integral for viscous heating due to slip in the tangential velocity component on a surface. Definitions of the input parameters are as follows:

Q_VELO_SLIP	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.

Examples¶

The following is a sample input card:

BC = Q_VELO_SLIP_BC SS 10

Technical Discussion¶

Use of this boundary condition requires specification of the slip velocity components by using either the VELO_SLIP or VELO_SLIP_ROT boundary condition.

Q_LASER_WELD¶

BC = Q_LASER_WELD SS <bc_id> <float_list>

Description / Usage¶

(WIC/ENERGY)

This boundary condition card specifies the thermal boundary conditions for laser welding. The <float_list> requires twenty-seven values be specified; definitions of the input parameters are as follows:

Q_LASER_WELD	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	Nominal power of laser.
<float2>	Power of laser at base state (simmer).
<float3>	Base value of surface absorptivity.
<float4>	Switch to allow tracking of normal component of liquid surface relative to laser beam axis for surface absorption (0 = OFF, 1 = ON)
<float5>	Cutoff time for laser power.
<float6>	Time at which laser power drops to 1/e.
<float7>	For pulse weld, the laser power overshoot (%) of peak power at time to reach peak laser power.
<float8>	Radius of laser beam.
<float9>	For pulse weld, the time for laser pulse to reach peak power.
<float10>	For pulse weld, the time for laser pulse to reach steady state in power.
<float11>	Switch to either activate laser power distribution from beam center based on absolute distance (0) or based on radial distance in 2D plane (1).
<float12>	Location of laser beam center (x-coordinate).
<float13>	Location of laser beam center (y-coordinate).
<float14>	Location of laser beam center (z-coordinate).
<float15>	Laser beam orientation, normal to x-coordinate of body.
<float16>	Laser beam orientation, normal to y-coordinate of body.
<float17>	Laser beam orientation, normal to z-coordinate of body.
<float18>	For pulse weld, spot frequency.
<float19>	For pulse weld, total number of spots to simulate.
<float20>	Switch to set type of weld simulation. (0=pulse weld, 1=linear continuous weld, -1=pseudo pulse weld, 2=sinusoidal continous weld)
<float21>	For pulse weld, spacing of spots.
<float22>	For radial traverse continuous weld, radius of beam travel.
<float23>	Switch to activate beam shadowing for lap weld (0=OFF, 1=ON). Currently only active for ALE simulations.
<float24>	Not active, should be set to zero.
<float25>	For continuous weld, laser beam travel speed in xdirection (u velocity).
<float26>	For continuous weld, laser beam travel speed in ydirection (v velocity).
<float27>	For continuous weld, laser beam travel speed in zdirection (w velocity).

Examples¶

The following is a sample input card:

BC = Q_LASER_WELD SS 10 4.774648293 0 0.4 1 1 1.01 4.774648293 0.2
0.01 0.01 1 0.005 0 -0.198 -1 0 0 0.025 1 1 0.2032 -1000 0 0 0 0 0.0254

Technical Discussion¶

Several required pieces of information to use this boundary condition are not in final form, and the user can expect future changes and improvements. Below is a listing of some of these parameters:

This boundary condition requires that node sets 1001 is defined in the EXODUS II file. NS 1001 should include the point at the center of the keyhole on the surface closest to the beam.
Currently the laser flux distribution is set as a fixed exponential distribution. Plans are to include more options including a user-defined exponential and a TABLE option.
Correlations are used to specify the evaporation energy loss. Currently only iron and ice correlations exist; the appropriate correlation is selected based on the value set for the Solidus Temperature (in Thermal Properties portion of the material file).

Q_VAPOR_BC¶

BC = Q_VAPOR SS <bc_id> <float_list>

Description / Usage¶

(WIC/ENERGY)

This boundary condition card is used to specify heat loss due to evaporation. It is typically used in conjunction with Q_LASER_WELD.

Q_VAPOR	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	Temperature scale.
<float2>	Energy unit scale.

Examples¶

The following is a sample input card:

BC = Q_VAPOR SS 10 100. 10.

Technical Discussion¶

This condition is turned on above the boiling point, which is story in the melting point solidus temperature.

VP_EQUIL¶

BC = VP_EQUIL SS <bc_id> <integer_list> <float>

Description / Usage¶

(SIC/ENERGY)

This boundary condition card is used to equate solvent partial pressure in the gas between the porous medium and the external phase. The condition is similar to the solid-liquid interface conditions that apply to interfaces between a porous medium and an external gas phase (in which the energy equation is used to solve for solvent concentration in the gas phase). This boundary condition is still under development.

There are three values to be specified for the <integer_list>; definitions of the input parameters are as follows:

VP_EQUIL	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer1>	Element block ID of solid, porous phase from the EXODUS II database.
<integer2>	Element block ID of gas phase from the EXODUS II database.
<integer3>	Species number of liquid phase in porous medium.
<float>	Ambient pressure in external gas phase.

Examples¶

The following is a sample input card:

BC = VP_EQUIL SS 100   1 2 0 0.0

where the solid/porous phase is present in element block 1 and the gas phase is present in element block 2. The external gas phase pressure has been set to 0.0.

Technical Discussion¶

No Discussion.

LATENT_HEAT¶

BC = LATENT_HEAT SS <bc_id> <integer> <float_list>

Description / Usage¶

(WIC/ENERGY)

This boundary condition card is used for latent heat release/adsorption at an external interface. The flux quantity is specified on a per mass basis so the heat and mass transfer coefficients are in units of L/t.

The <float_list> has three values to be specified; definitions of the input parameters are as follows:

LATENT_HEAT	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer>	Species number.
<float1>	Latent Heat for the pure w+1 species component.
<float2>	Mass transfer coefficient for the w+1 species component.
<float3>	Sink concentration for the w+1 species component.

The float values on this card apply to the bulk species (i.e., the w+1 component) in a multi-species problem and in the case of a pure fluid. Important usage comments are contained in the Technical Discussion below.

Examples¶

The following is a sample input card:

BC = LATENT_HEAT SS 3 0   540. 0.1   0.

Two more detailed examples are contained in the Technical Discussion section.

Technical Discussion¶

The LATENT_HEAT boundary condition has the form

where \(\underline{n}\) is the outward normal to the surface, \(\underline{q}\) is the heat flux vector, \(\Delta\) \(H_\nu\) is the heat of vaporization, \(\rho\) is density, \(h_i\) is the heat-transfer coefficient for species i, and \(y^0_i\) is the reference concentration of species i at locations remote from the boundary; the summation is over the number of species in the material block. The manner of usage of this boundary condition depends on the set of conditions characterizing the problem; example conditions are described below.

This card is used for external surfaces for which heat transfer and mass transfer beyond it’s surfaces are governed by heat and mass transfer coefficients. The LATENT_HEAT BC is applied to the energy equation so a heat flux can be specified for thermal problems alone. The mass transfer portion of the vaporization phenomenon is handled by the KIN_LEAK and YFLUX BC cards; these boundary conditions are applied to the mesh equations. The LATENT_HEAT_INTERNAL card should be used for internal surfaces, or interfaces, at which transfer is governed by actual physics being modeled as a part of the problem.

When vaporization of a pure liquid is being modeled, there is only a ’single species’, the bulk volatile liquid. In the single species case, the Species Properties of the corresponding material file (which includes the Heat of Vaporization card) is not even read so the actual value of the latent heat of vaporization must be entered on the*LATENT_HEAT* card (<float1>). If multiple species are present, the latent heat value for each species is entered in the material file and the LATENT_HEAT card does for the energy equation the same thing the KIN_LEAK card does for the mesh equation (i.e., collects the flux conditions that apply for each species).

For mass transfer in the single species/pure liquid case, the mass transfer coefficient is specified on the KIN_LEAK card. When multiple species are present, the mass transfer coefficient and driving concentration on the KIN_LEAK card are set to zero and the appropriate coefficient and driving concentration are set for each species on the YFLUX card, one for each species. The KIN_LEAK card (or the LATENT HEAT for energy flux) must be present to signal Goma to look for multiple YFLUX cards.

The latent heat quantity is specified on a per mass basis and the transfer coefficients are in units of L/t. Some examples of LATENT_HEAT application follow:

Pure Liquid Case

BC = LATENT HEAT   SS 3 0   540.   0.1   0.

BC = KIN_LEAK   SS 3   0.1   0.

Two-Species Case

BC = LATENT HEAT   SS 3 0   0.   0.1   0.

BC = KIN_LEAK   SS 3   0.   0.

BC = YFLUX SS 3 0   0.12   0.

BC = YFLUX   SS 3 1   0.05   0.

plus, in the corresponding material file:

---Species Properties
Diffusion Constitutive Equation= FICKIAN
Diffusivity = CONSTANT   0   1.e-8
Latent Heat Vaporization = CONSTANT   0   540.
Latent Heat Fusion = CONSTANT   0   0.
Vapor Pressure = CONSTANT   0   0.
Species Volume Expansion = CONSTANT   0   1.
Reference Concentration = CONSTANT   0   0.
Diffusivity = CONSTANT   1   1.e-6
Latent Heat Vaporization = CONSTANT   1   125.
Latent Heat Fusion = CONSTANT   1   0.
Vapor Pressure = CONSTANT   1   0.
Species Volume Expansion = CONSTANT   1   1.
Reference Concentration = CONSTANT   1   0.

References¶

No References.

LATENT_HEAT_INTERNAL¶

BC = LATENT_HEAT_INTERNAL SS {char_string} <integer_list> <float>

Description / Usage¶

(WIC/ENERGY)

This boundary condition card is used for latent heat release/adsorption at an internal interface. See usage comments in the Technical Discussion.

The <integer_list> requires two values be specified; definitions of the input parameters are as follows:

LATENT_HEAT_INTERNAL	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
{char_string}	Variable name with the following permissible values: LIQUID_VAPOR SOLID_LIQUID
<integer1>	NOT ACTIVE. Any integer will do.
<integer2>	NOT ACTIVE. Any integer will do.
<float3>	Value of latent heat of vaporization/fusion for a pure material case, in units of Energy/mass.

Examples¶

The following is a sample input card:

BC = LATENT_HEAT_INTERNAL SS 40 SOLID_LIQUID 1 2 2.6e5

Technical Discussion¶

The LATENT_HEAT_INTERNAL card should be used for internal surfaces, or interfaces, at which transfer is governed by actual physics being modeled as a part of the problem. See LATENT_HEAT card for further information.

Category 6: Mass Equations¶

The collection of boundary conditions in this category are applied to the mass balance equations, specifically the species component balance equations. Most boundary conditions are weakly integrated conditions defining fluxes at internal or external surfaces, although strongly integrated and Dirichlet conditions are also available to control known values of dependent variables or integrated quantities. Boundary conditions are available for chemical species as well as charged species, suspensions and liquid metals. An important capability in Goma is represented by the discontinuous variable boundary conditions, for which users are referred to Schunk and Rao (1994) and Moffat (2001). Care must be taken if the species concentration is high enough to be outside of the dilute species assumption, in which case transport of species through boundaries will affect the volume of the bounding fluids. In these cases, users are referred to the VNORM_LEAK condition for the fluid momentum equations and to KIN_LEAK for the solid momentum (mesh) equations. And finally, users are cautioned about different bases for concentration (volume, mass, molar) and several discussions on or references to units.

Y¶

BC = Y NS <bc_id> <integer> <float1> [float2] [integer2]

Description / Usage¶

(DC/MASS)

This card is used to set the Dirichlet boundary condition of constant concentration for a given species. Definitions of the input parameters are as follows:

Y	Name of the boundary condition (<bc_name>).
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<integer1>	Species number of concentration.
<float1>	Value of concentration, in user’s choice of units, e.g. moles/ \(cm^3\).
[float2]	An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.
[integer2]	Element block ID; only applicable to node sets, this optional parameter specifies the element block on which to impose the boundary condition, if there is a choice, as occurs at discontinuous variable interfaces where there may be more that one unknown corresponding to species 0 at a single node. This parameter allows the user to specify which unknown to set the boundary condition on, and allows for a jump discontinuity in species value across a discontinuous variables interface.

Examples¶

The following is a sample card with no Dirichlet flag:

BC = Y NS 3   0   0.00126

Technical Discussion¶

No Discussion.

YUSER¶

BC = YUSER SS <bc_id> <integer> <float_list>

Description / Usage¶

(SIC/MASS)

This is a user-defined mass concentration boundary. The user must supply the relationship in function yuser_surf within user_bc.c.

YUSER	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<integer>	Species number.
<float_list>	A list of float values separated by spaces which will be passed to the user-defined subroutines so the user can vary the parameters of the boundary condition. This list of float values is passed as a one-dimensional double array to the appropriate C function.

Examples¶

The following sample input card applies a user flux condition to side set 100 for species 0 that requires two input parameters:

BC = YUSER SS 100 0 .5 .5

Technical Discussion¶

No Discussion.

References¶

No References.

Y_DISCONTINUOUS¶

BC = Y_DISCONTINUOUS NS <bc_id> <integer1> <float1> [float2 integer2]

Description / Usage¶

(DC/MASS)

This card is used to set a constant valued Dirichlet boundary condition for the species unknown. The condition only applies to interphase mass, heat, and momentum transfer problems applied to discontinuous (or multivalued) species unknown variables at an interface, and it must be invoked on fields that employ the Q1_D or Q2_D interpolation functions to “tie” together or constrain the extra degrees of freedom at the interface in question.

Definitions of the input parameters are as follows:

Y_DISCONTINUOUS	Name of the boundary condition (<bc_name>).
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<integer1>	Species subvariable number.
<float1>	Value of the species unknown on the boundary. Note, the units depend on the specification of the type of the species unknown.
[float2]	An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.
[integer2]	Element block ID; only applicable to node sets, this optional parameter specifies the element block on which to impose the boundary condition, if there is a choice, as occurs at discontinuous variable interfaces where there may be more that one unknown corresponding to species 0 at a single node. This parameter allows the user to specify which unknown to set the boundary condition on, and allows for a jump discontinuity in species value across a discontinuous variables interface.

Examples¶

The following is a sample input card with no Dirichlet flag:

BC = Y_DISCONTINUOUS SS 3   0   0.00126

Technical Discussion¶

Typically, this boundary condition may be used to set the species unknown variable on one side of a discontinuous variables interface, while the species unknown variable on the other side of the interface is solved for via a KINEMATIC_SPECIES boundary condition. Note, this boundary condition is not covered by the test suite, and thus, may or may not work.

YFLUX¶

BC = YFLUX SS <bc_id> <integer1> <float1> <float2>

Description / Usage¶

(WIC/MASS)

This boundary condition card is used to specify the mass flux of a given species normal to the boundary (or interface) using a mass transfer coefficient. When used in conjunction with the KIN_LEAK card, the YFLUX card also enables the determination of velocity normal to the moving boundary at which the YFLUX boundary condition is applied.

Definitions of the input parameters are as follows:

YFLUX	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer>	i, species number of concentration.
<float1>	\(k_i\), value of mass transfer coefficient of species i.
<float2>	\(c_i^\infty\) value of reference concentration of species i.

Examples¶

Following are two sample cards:

BC = YFLUX SS   3 0   0.12   0.

BC = YFLUX SS   3 1   0.05   0.

Technical Discussion¶

Specifically, the species mass flux is given by

where n is the unit vector normal to the boundary, \(J_i\) is mass flux of species i, v is the fluid velocity, \(v_m\) is the mesh displacement velocity, \(k_i\) is mass transfer coefficient of species i, \(c_i\) is concentration of species i at the boundary surface, \(c_i^\infty\) and is reference concentration of species i. The units of \(J_i\), \(k_i\), \(c_i\) and \(c_i^\infty\) depend on the user’s choice. For example, if \(c_i\) and \(c_i^\infty\) are chosen to have units of moles/ \(cm^3\), then \(k_i\) has the unit of cm/ s, and \(J_i\) has the units of moles/ \(cm^2\) /s.

For the KIN_LEAK and VNORM_LEAK cards, the information from YFLUX boundary conditions corresponding to each species is needed. Goma automatically searches for these boundary conditions and uses an extra variable in the BC data storage to record the boundary condition number of the next YFLUX condition in a linked list; when the extra storage value is -1, there are no more YFLUX conditions at this boundary.

FAQs¶

A question was raised regarding the use of volume flux in Goma; the following portion of the question and response elucidate this topic and the subject of units. Note the references in the response are to the Version 2.0 Goma User’s Manual.

Question: … I know what you are calling volume flux is mass flux divided by density. The point I am trying to make is that the conservation equations in the books I am familiar with talk about mass, energy, momentum, and heat fluxes. Why do you not write your conservation equations in their naturally occurring form? If density just so happens to be common in all of the terms, then it will be obvious to the user that the problem does not depend on density. You get the same answer no matter whether you input rho=1.0 or rho=6.9834, provided of course this does not impact iterative convergence. This way, you write fluxes in terms of gradients with the transport properties (viscosity, thermal conductivity, diffusion coefficient, etc.) being in familiar units.

Answer: First let me state the only error in the manual that exists with regard to the convection-diffusion equation is the following:

\(J_t\) in the nomenclature table … should be described as a volume flux with units of L/t, i.e., \(D ⋅ \Delta_yi\) , where D is in \(L^2\) ⁄ t units.

Now, … this is actually stated correctly, as it states the \(J_i\) is a diffusion flux (without being specific); to be more specific here, we should say it is a “volume flux of species i.” So, in this case D is in L ⋅ L ⁄ t units, \(y_i\) is dimensionless and it is immaterial that (the mass conservation equation) is multiplied by density or not, as long as density is constant.

Now, in Goma we actually code it up EXACTLY as in the … (mass conservation equation), i.e., there are no densities anywhere for the FICKIAN diffusion model. For the HYDRO diffusion model, we actually compute a \(J_i\) ⁄ ρ in the code, and handle variable density changes through that p . In that case \(J_i\) as computed in Goma is a mass flux vector, not a volume flux vector, but by dividing it by p and sending it back up to the mass conservation equation it changes back into a volume flux. i. e., everything is the same.

Concerning the units of the mass transfer coefficient on the YFLUX boundary condition, the above discussion now sets those. Goma clearly needs the flux in the following form:

and dimensionally for the left hand side

where D is in units \(L^2\) /t , the gradient operator has units of 1/L so K HAS to be in units of L/t (period!) because \(y_i\) is a fraction.

So, if you want a formulation as follows:

then K’s units will have to accommodate for the relationship between \(p_i\) and \(y_i\) in the liquid, hopefully a linear one as in Raoult’s law, i.e. if \(p_i\) = \(P_V\)\(y_i\) where \(P_v\) is the vapor pressure, then

and so K on the YFLUX command has to be \(KP_v\) ….and so on.

Finally, you will note, since we do not multiply through by density, you will have to take care of that, i. e., in the Price paper he gives K in units of t/L. So, that must be converted as follows:

This checks out!

References¶

Price, P. E., Jr., S. Wang, I. H. Romdhane, 1997. “Extracting Effective Diffusion Parameters from Drying Experiments”, AIChE Journal, 43, 8, 1925-1934.

YFLUX_CONST¶

BC = YFLUX_CONST SS <bc_id> <integer> <float>

Description / Usage¶

(WIC/MASS)

This boundary condition card is used to specify a constant diffusive mass flux of a given species. This flux quantity can be specified on a per mass basis (e.g. with units of g/ \(cm^2\) /s) or on a per mole basis (e.g. with units of moles/ \(cm^2\) /s), depending on the user’s choice of units in the species unknown.

Definitions of the input parameters are as follows:

YFLUX_CONST	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer>	Species number.
<float>	Value of diffusive mass flux; the units of this quantity depends on the user’s choice of units for species concentration.

Examples¶

Following is a sample card:

BC = YFLUX_CONST SS 1 0 10000.2

Technical Discussion¶

No Discussion.

References¶

No References.

YFLUX_EQUIL¶

BC = YFLUX_EQUIL SS <bc_id> {char_string} <integer> <float_list>

Description / Usage¶

(WIC/MASS)

This boundary card is used when equilibrium-based mass transfer is occurring at an vapor-liquid external boundary; i.e.,

This is different from an internal boundary since only one phase is represented in the computational domain. This boundary condition then describes the rate of mass entering or leaving the boundary via vapor-liquid equilibria. The \(w_i^v\) is the mass fraction of component i in \(\underline{vapor}\) that is in equilibrium with the liquid phase. The \(w_i^{v \infty}\) is the bulk concentration of component i in vapor.

The <float_list> requires three input values; definitions of the input parameters are as follows:

YFLUX_EQUIL	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
{char_string}	This refers to the equilibrium model for mass transfer; the options are either FLORY or RAOULT.
<integer1>	Species id.
<float1>	Total system pressure.
<float2>	Mass transfer coefficient.
<float3>	Bulk concentration in vapor ( \(w_i^{v \infty}\) )

Examples¶

The following is a sample input card:

BC = YFLUX_EQUIL SS 1   FLORY 0   1. 5.4e-3   0.

Technical Discussion¶

This boundary condition is very similar to VL_EQUIL and VL_POLY except that it is only applied at an external boundary where vapor phase is not modeled in the problem.

References¶

GTM-007.1: New Multicomponent Vapor-Liquid Equilibrium Capabilities in GOMA, December 10, 1998, A. C. Sun

YFLUX_SULFIDATION¶

BC = YFLUX_SULFIDATION SS <bc_id> {char_string} <integer> <float_list>

Description / Usage¶

(WIC/MASS)

The YFLUX_SULFIDATION card enables computation of the molar flux of the diffusing species (e.g. copper vacancy) using copper-sulfidation kinetics at the specified boundary (gas/ \(Cu^2S\) or Cu/ \(Cu^2S\) interface). When used in conjunction with the KIN_LEAK card, it also enables the determination of velocity normal to the moving gas/ \(Cu^2S\) interface.

The <float_list> contains ten values to be defined; these and all input parameter definitions are as follows:

YFLUX_SULFIDATION	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
{char_string}	Name of sulfidation kinetic models. Allowable names are: SOLID_DIFFUSION_SIMPLIFIED SOLID_DIFFUSION SOLID_DIFFUSION_ELECTRONEUTRALITY SOLID_DIFFUSION_ELECTRONEUTRALITY_LINEAR GAS_DIFFUSION FULL ANNIHILATION ANNIHILATION_ELECTRONEUTRALITY Detailed description of kinetic models with these name key words are presented in the Technical Discussion section below.
<integer>	Species number of concentration.
<float1>	Stoichiometric coefficient.
<float2>	Rate constant for forward copper sulfidation reaction.
<float3>	Activation energy for forward copper sulfidation reaction.
<float4>	Rate constant for backward copper sulfidation reaction.
<float5>	Activation energy for backward copper sulfidation reaction.
<float6>	Temperature.
<float7>	Bulk concentration of \(H^2S\)
<float8>	Bulk concentration of \(O^2\)
<float9>	Molecular weight of copper sulfide ( \(Cu_2S\) )

Examples¶

Examples of this input card follow:

BC = YFLUX_SULFIDATION SS 3 SOLID_DIFFUSION_ELECTRONEUTRALITY 0 -2.0
1.46e+7 6300.0 1.2e+14 6300.0 303.0 1.61e-11 8.4e-6 159.14 5.6

BC = YFLUX_SULFIDATION SS 1 ANNIHILATION_ELECTRONEUTRALITY 0 1.0   10.0
0.0   0.0   0.0   303.0 1.61e-11 8.4e-6 159.14 5.6

BC = YFLUX_SULFIDATION SS 3 SOLID_DIFFUSION 1 -2.0 1.46e7 6300.0 1.2e+14
6300.0 303.0 1.61e-11 8.4e-6 159.14 5.6

BC = YFLUX_SULFIDATION SS 1 ANNIHILATION 1 1.0 10.0   0.0   0.0   0.0
303.0 1.61e-11 8.4e-6 159.14 5.6

Technical Discussion¶

Key word SOLID_DIFFUSION_SIMPLIFIED refers to the following simplified kinetic model of copper sulfidation in which gas-phase diffusion is neglected and Cu is taken to be the diffusing species:

where r is molar rate of formation of sulfidation-corrosion product, \(Cu^2S\), per unit area, \(^cH_2S\) is the molar concentration of \(H_2S\) taken to be fixed at its bulk value, \(^cCu\) is the molar concentration of Cu at the sulfidation surface ( \(Cu_2S\) /gas interface), k is the rate constant, E is the activation energy, R is the universal gas constant, and T is the temperature.

Key word SOLID_DIFFUSION refers to the following kinetic model of copper sulfidation in which gas-phase diffusion is neglected and Cu vacancies and electron holes are taken as the diffusing species:

where r is molar rate of formation of \(Cu_2S\) per unit area, \(^cH_2S\) and \(^cO_2\) are the molar concentrations of \(H_2S\) and \(O_2\), respectively, taken to be fixed at their bulk values, \(^c_V\) and \(^c_h\) are the molar concentrations of Cu vacancies and electron holes, respectively, at the sulfidation surface, \(k_1\) and \(k_{-1}\) are rate constants, respectively, for the forward and backward sulfidation reactions, \(E_1\) and \(E_{-1}\) are activation energies, respectively, for the forward and the backward sulfidation reactions.

Key word SOLID_DIFFUSION_ELECTRONEUTRALITY refers to the following kinetic model of copper sulfidation in which Cu vacancies and electron holes are taken as the diffusing species and the electroneutrality approximation is applied such that concentrations of Cu vacancies and electron holes are equal to each other:

Key word SOLID_DIFFUSION_ELECTRONEUTRALITY_LINEAR refers to the following kinetic model of copper sulfidation:

Key word GAS_DIFFUSION refers to the following simplified kinetic model of copper sulfidation in which solid-phase diffusion is neglected, and \(H_2S\) and \(O_2\) are taken to be the diffusing species:

Key word FULL refers to the following kinetic model in which diffusion in both the gas phase and the solid phase are important, and \(H_2S\), \(O_2\), Cu vacancies, and electron holes are taken as the diffusing species:

where \(^cH_2S\) and \(^cO_2\) are the time-dependent molar concentrations of \(H_2S\) and \(O_2\), respectively, at the sulfidation surface.

Key word ANNIHILATION refers to the following kinetic model in which diffusion in both the gas phase and the solid phase are important, and \(H_2S\), \(O_2\), Cu vacancies, and electron holes are taken as the diffusing species:

where \(k_2\) are \(E_2\) are the rate constant and activation energy, respectively, for the annihilation reaction.

Key word ANNIHILATION_ELECTRONEUTRALITY is similar to ANNIHILATION except that, here, the electroneutrality approximation is applied and concentrations of Cu vacancies and electron holes are taken to be equal to each other:

YFLUX_SUS¶

BC = YFLUX_SUS SS <bc_id> <integer>

Description / Usage¶

(WIC/MASS)

This boundary defines a flux of suspension particles at an interface. Definitions of the input parameters are as follows:

YFLUX_SUS	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer>	Species id; the species number for suspension particles.

Examples¶

The following is a sample input card:

BC = YFLUX_SUS SS 1   0

Technical Discussion¶

This condition is only used in conjunction with the SUSPENSION liquid constitutive models, HYDRODYNAMIC diffusivity model, and SUSPENSION or SUSPENSION_PM density models. A theoretical outflux condition associated with suspension particles leaving the domain is tied to the Phillips diffusive-flux model. Please refer to discussions on HYDRODYNAMIC diffusivity to gain more understanding of the suspension flux model.

YFLUX_BV¶

BC = YFLUX_BV SS <bc_id> <integer1> <floatlist>

Description / Usage¶

(WIC/MASS)

The YFLUX_BV card enables computation of the molar flux of the specified species using Butler-Volmer kinetics at the specified boundary (namely, the electrode surface). When used in conjunction with the KIN_LEAK card, it also enables the determination of velocity normal to the moving solid-electrode surface.

The <floatlist> consists of nine values; definitions of the input parameters are as follows:

YFLUX_BV	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer1>	Species number of concentration.
<float1>	Stoichiometric coefficient.
<float2>	Kinetic rate constant.
<float3>	Reaction order.
<float4>	Anodic direction transfer coefficient.
<float5>	Cathodic direction transfer coefficient.
<float6>	Electrode potential or applied voltage.
<float7>	Theoretical open-circuit potential.
<float8>	Molecular weight of solid deposit.
<float9>	Density of solid deposit.

Examples¶

The following is a sample input card:

BC = YFLUX_BV SS 1 0 -1. 0.00001 1. 0.21 0.21 -0.8 -0.22 58.71 8.9

Technical Discussion¶

No Discussion.

YFLUX_HOR¶

BC = YFLUX_HOR SS <bc_id> <integer> <floatlist>

Description / Usage¶

(WIC/MASS)

The YFLUX_HOR card enables computation of the molar flux of the specified species at the specified boundary (i.e., at the electrode surface) using the linearized Butler- Volmer kinetics such as that for the hydrogen-oxidation reaction in polymerelectrolyte- membrane fuel cells.

The <floatlist> consists of 10 values; definitions of the input parameters are as follows:

YFLUX_HOR	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer>	Species number of concentration.
<float1>	Product of interfacial area per unit volume by exchange current density, \(ai_0\), in units of \(A/cm^3\).
<float2>	Catalyst layer or catalyzed electrode thickness, H, in unit of cm.
<float3>	Reference concentration, \(c_{ref}\), in units of moles/ \(cm^3\).
<float4>	Anodic direction transfer coefficient, \(\alpha_a\).
<float5>	Cathodic direction transfer coefficient, \(\alpha_c\).
<float6>	Temperature, T, in unit of K.
<float7>	Theoretical open-circuit potential, \(U_0\), in unit of V.
<float8>	Reaction order, \(\beta\).
<float9>	Number of electrons involved in the reaction, n.
<float10>	Electrode potential, V, in unit of V.

Examples¶

The following is a sample input card:

BC = YFLUX_HOR SS 14 0 1000. 0.001 4.e-5 1. 1. 353. 0. 0.5 2. 0.

Technical Discussion¶

For electrochemical reactions such as the hydrogen-oxidation reaction (HOR), surface overpotential is relatively small such that the Butler-Volmer kinetic model can be linearized to yield:

where r is the surface reaction rate in units of moles/ \(cm^2-s\); \(ai_0\) denotes the product of interfacial area per unit volume by exchange current density, which has units of \(A/cm^3\); H is the catalyst layer or catalyzed electrode thickness in unit of cm; n is the number of electrons involved in the electrochemical reaction; R is the universal gas constant ( \(\equiv\) 8.314 J/mole-K); T is temperature in unit of K; c and \(c_{ref}\) are, respectively, species and reference molar concentrations in units of moles/ \(cm^3\); \(\beta\) is reaction order; \(\alpha_a\) and \(\alpha_c\) are, respetively, the anodic and cathodic transfer coefficients; V and \(\phi\) are, respectively, the electrode and electrolyte potentials in unit of V; \(U_0\) and is the opencircuit potential in unit of V.

References¶

Newman, Electrochemical Systems, 2nd Edition, Prentice-Hall, NJ (1991).

K. S. Chen and M. A. Hickner, “Modeling PEM fuel cell performance using the finiteelement method and a fully-coupled implicit solution scheme via Newton’s technique”, in ASME Proceedings of FUELCELL2006-97032 (2006).

YFLUX_ORR¶

BC = YFLUX_ORR SS <bc_id> <integer> <floatlist>

Description / Usage¶

(WIC/MASS)

The YFLUX_ORR card enables computation of the molar flux of the specified species at the specified boundary (i.e., at the electrode surface) using the Tafel kinetics such as that for the oxygen-reduction reaction in polymer-electrolyte-membrane fuel cells.

The <floatlist> consists of 9 values; definitions of the input parameters are as follows:

YFLUX_ORR	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer>	Species number of concentration.
<float1>	Product of interfacial area per unit volume by exchange current density, \(ai_0\), in units of \(A/cm^3\).
<float2>	Catalyst layer or catalyzed electrode thickness, H, in unit of cm.
<float3>	Reference concentration, \(c_{ref}\), in units of moles/ \(cm^3\).
<float4>	Cathodic direction transfer coefficient, \(\alpha_c\).
<float5>	Temperature, T, in unit of K.
<float6>	Electrode potential, V, in unit of V.
<float7>	Theoretical open-circuit potential, \(U_0\), in unit of V.
<float8>	Reaction order, \(\beta\).
<float9>	Number of electrons involved in the reaction, n.

Examples¶

The following is a sample input card:

BC = YFLUX_ORR SS 15 1 0.01 0.001 4.e-5 1. 353. 0.7 1.18 1. 4.

Technical Discussion¶

For electrochemical reactions such as the hydrogen-oxidation reaction (HOR), surface overpotential is relatively small such that the Butler-Volmer kinetic model can be linearized to yield:

where r is the surface reaction rate in units of moles/ \(cm^2-s\); \(ai_0\) denotes the product of interfacial area per unit volume by exchange current density, which has units of A/ \(cm^3\); H is the catalyst layer or catalyzed electrode thickness in unit of cm; n is the number of electrons involved in the electrochemical reaction; F is the Faraday’s constant ( \(\equiv\) 96487 C/mole); c and \(c_{ref}\) are, respectively, species and reference molar concentrations in units of moles/ \(cm^3\); \(\beta\) is reaction order; \(\alpha_c\) is the anodic and cathodic transfer coefficient; R is the universal gas constant ( \(\equiv\) 8.314 J/mole-K); T is temperature in unit of K; V and \(\phi\) are, respectively, the electrode and electrolyte potentials in unit of V; \(U_0\) and is the open-circuit potential in unit of V.

References¶

Newman, Electrochemical Systems, 2nd Edition, Prentice-Hall, NJ (1991).

K. S. Chen and M. A. Hickner, “Modeling PEM fuel cell performance using the finiteelement method and a fully-coupled implicit solution scheme via Newton’s technique”, in ASME Proceedings of FUELCELL2006-97032 (2006).

YFLUX_USER¶

BC = YFLUX_USER SS <bc_id> <integer> <float_list>

Description / Usage¶

(WIC/MASS)

This boundary condition card is used to set mass flux to a user-prescribed function and integrate by parts again. The user should provide detailed flux conditions in the mass_flux_user_surf routine in user_bc.c. The flux quantity is specified on a per mass basis so the heat and mass transfer coefficients are in units of L/t.

Definitions of the input parameters are as follows:

YFLUX_USER	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer>	Species number of concentration.
<float_list>	A list of float values separated by spaces which will be passed to the user-defined subroutines so the user can vary the parameters of the boundary condition. This list of float values is passed as a one-dimensional double array to the appropriate C function.

Examples¶

The following is a sample input card:

BC = YFLUX_USER SS 2   0 .5 .5

Technical Discussion¶

No Discussion.

References¶

No References.

YFLUX_ALLOY¶

BC = YFLUX_ALLOY SS <bc_id> <integer1> <float_list>

Description / Usage¶

(WIC/MASS)

This boundary condition card calculates the surface integral for a mass flux transfer model for the evaporation rate of molten metal.

The <float_list> requires six values; definitions of the input parameters are as follows:

YFLUX_ALLOY	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer1>	Species number.
<float1>	Liquidus temperature of metal alloy, \(T_m\).
<float2>	Base Concentration, \(y^\infty\).
<float3>	Coefficient \(c_0\).
<float4>	Coefficient \(c_1\).
<float5>	Coefficient \(c_2\).
<float6>	Coefficient \(c_3\).

Examples¶

The following is a sample input card:

BC = YFLUX_ALLOY SS 10 0 1623.0 0.5 0.01 -1e-3 1e-4 -1e-5

Technical Discussion¶

Basically the difference between this model and the simple convective mass transfer coefficient (say \(k_i\) for YFLUX) is that the transfer coefficient here (the exponential term) has a cubic dependence on temperature.

YTOTALFLUX_CONST¶

BC = YTOTALFLUX_CONST SS <bc_id> <integer> <float>

Description / Usage¶

(WIC/MASS)

This boundary condition card is used to specify a constant total mass flux (including contribution from diffusion, migration, and convection) of a given species. This card enables the treatment of the situation in which diffusion, migration and convection fluxes cancel each other such that the total flux vanishes (e.g. is equal to zero). This flux quantity can be specified on a per mass basis (i.e., with units of g/ \(cm^2\)/s) or on a per mole basis (e.g. with units of moles/\(cm^2\)/s), depending on the user’s choice of units in the species concentration unknown.

Definitions of the input parameters are as follows:

YTOTALFLUX_CONST	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer>	Species number of concentration.
<float>	Value of total mass flux - the units of this quantity depends on the user’s choice of units for species concentration.

Examples¶

Following is a sample card:

BC = YTOTALFLUX_CONST SS 5   0   0.0

Technical Discussion¶

No Discussion.

VL_EQUIL¶

BC = VL_EQUIL SS <bc_id> <integer_list> <float_list>

Description / Usage¶

(SIC/MASS)

This boundary condition card enforces vapor-liquid equilibrium between a gas phase and a liquid phase using Raoult’s law. The condition only applies to interphase mass, heat, and momentum transfer problems with discontinuous (or multivalued) variables at an interface, and it must be invoked on fields that employ the Q1_D or Q2_D interpolation functions to “tie” together or constrain the extra degrees of freedom at the interface in question.

The <integer_list> has three values and the <float_list> has five values; definitions of the input parameters are as follows:

VL_EQUIL	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer1>	Species number.
<integer2>	Element block ID of liquid phase.
<integer3>	Element block ID of gas phase.
<float1>	Base ambient pressure in gas phase.
<float2>	Molecular weight of first volatile species.
<float3>	Molecular weight of second volatile species.
<float4>	Molecular weight of condensed phase.
<float5>	Molecular weight of insoluble gas phase.

This boundary condition is applied to ternary, two-phase flows that have rapid mass exchange between phases, rapid enough to induce a diffusion velocity at the interface, and to thermal contact resistance type problems. The best example of this is rapid evaporation of a liquid component into a gas. In the current discontinuous mass transfer model, we must require the same number of components on either side of interface. In this particular boundary, two of three components are considered volatile, so they participate in both vapor and liquid phases. The third component is considered either non-volatile or non-condensable, so it remains in a single phase.

Examples¶

A sample input card follows for this boundary condition:

BC = VL_EQUIL SS 4 0 1 2 1.e+06 28. 18. 1800. 18.

The above card demonstrates these characteristics: species number is “0”; liquid phase block id is 1; gas phase block id is 2; ambient pressure is 1.e6 Pa; the molecular weights of the volatile species are 28 and 18; of the condensed phase and insoluble portion of the gas phase, 1800 and 18, respectively.

Technical Discussion¶

One of the simplest forms of the equilibrium relation is the Raoult’s law, where the mole fraction of a species is equal to its mole fraction in the liquid multiplied by the ratio of its pure component vapor pressure to the total pressure in the system.

where \(y_i\) are the mole fraction of species i in the gas phase and \(x_i\) is the mole fraction in the liquid phase. The molecular weights required in this boundary card are used for converting mass fractions to mole fractions. The temperature dependency in the equilibrium expression comes from a temperature-dependent vapor pressure model. Either Riedel or Antoine temperature-dependent vapor pressure model can be specified in the VAPOR PRESSURE material card in order to link temperature to Raoult’s law.

References¶

GTM-007.1: New Multicomponent Vapor-Liquid Equilibrium Capabilities in GOMA, December 10, 1998, A. C. Sun

Schunk, P.R. and Rao, R.R. 1994. “Finite element analysis of multicomponent twophase flows with interphase mass and momentum transport,” IJNMF, 18, 821-842.

VL_POLY¶

BC = VL_POLY SS <bc_id> {char_string} <integer_list> <float>

Description / Usage¶

(SIC/MASS)

This boundary condition card enforces vapor-liquid equilibrium between a gas phase and a liquid phase using Flory-Huggins activity expression to describe polymer-solvent mixtures. The condition only applies to interphase mass, heat, and momentum transfer problems with discontinuous (or multivalued) variables at an interface, and it must be invoked on fields that employ the Q1_D or Q2_D interpolation functions to “tie” together or constrain the extra degrees of freedom at the interface in question.

There are three input values in the <integer_list>; definitions of the input parameters are as follows:

VL_POLY	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
{char_string}	the concentration basis; two options exist: MASS - the concentration variable in Goma is equivalent to mass fractions. VOLUME - the concentration variable in Goma is based on volume fractions for all species.
<integer1>	Species number of concentration.
<integer2>	Element block id that identifies the liquid phase.
<integer3>	Element block id that identifies the vapor phase.
<float>	Total pressure of the system.

Examples¶

This is a sample input card for this boundary condition:

BC = VL_POLY SS 7 MASS 0 1 2 1.e+05

Technical Discussion¶

One of the simplest forms of the equilibrium relation is the Raoult’s law, where the mole fraction of a species is equal to its mole fraction in the liquid multiplied by the ratio of its pure component vapor pressure to the total pressure in the system.

\(\gamma_i\) is defined as the activity coefficient of species i and is considered a departure function from the Raoult’s law. The fugacity in the liquid is reformulated in terms of volume fraction \(\phi_i\) for polymer mixtures to avoid referencing the molecular weight of polymer (Patterson, et. al., 1971).

Based on an energetic analysis of excluded volume imposed by the polymer, the activity coefficient model of Flory-Huggins is widely used for polymer-solvent mixtures (Flory, 1953). The general form of the Flory-Huggins model for multicomponent mixtures is a summation of binary interactions terms; i.e.,

\(v_i\) is the molar volume of component i (or the average-number molar volume if i is a polymer). \(\zeta_{ki}\) is the Dirac delta. \(\chi_{jk}\) is known as the Flory-Huggins interaction parameter between components j and k, and is obtainable by fitting the solubility data to the above model. For a simple binary pair (solvent (1)-polymer (2)) and assuming \(v_2\) » \(v_1\), the above model reduces to a simpler form.

References¶

Flory, P., Principles of Polymer Chemistry, Cornell University Press, New York (1953)

Patterson, D., Y.B. Tewari, H.P. Schreiber, and J.E. Guillet, “Application of Gas-Liquid Chromatography to the Thermodynamics of Polymer Solutions,”Macromolecules, 4, 3, 356-358 (1971)

GTM-007.1: New Multicomponent Vapor-Liquid Equilibrium Capabilities in GOMA, December 10, 1998, A. C. Sun

VL_EQUIL_PSEUDORXN¶

BC = VL_EQUIL_PSEUDORXN SS <bc_id> <integer_list> <float>

Description / Usage¶

(WIC/MASS)

This boundary condition card enforces vapor-liquid equilibrium between a gas phase and a liquid phase species component using Raoult’s law expressed via a finite-rate kinetics formalism. The condition only applies to problems containing internal interfaces with discontinuous (or multilevel) species unknown variables. The species unknown variable must employ the Q1_D or Q2_D interpolation functions in both adjacent element blocks. This boundary condition constrains the species equations on both sides of the interface (i.e., supplies a boundary condition) by specifying the interfacial mass flux on both sides.

Definitions of the input parameters are as follows:

VL_EQUIL_PSEUDORXN	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer1>	Species number.
<integer2>	Element Block ID of the liquid phase.
<integer3>	Element Block ID of the gas phase.
<float>	Rate constant for the forward reaction in units of length divided by time.

This boundary condition is typically applied to multicomponent two-phase flows that have rapid mass exchange between phases. The best example of this is rapid evaporation of a liquid component into a gas.

Examples¶

The following sample input card

BC = VL_EQUIL_PSEUDORXN SS 4 0 1 2 100.

demonstrates the following characteristics: species number is “0”; liquid phase element block id is “1”; gas phase element block id is “2”; a forward rate constant of 100.0 cm \(s^{-1}\).

Technical Discussion¶

The VL_EQUIL_PSEUDORXN boundary condition uses the following equations representing a kinetic approach to equilibrium expressed by Raoult’s law, relating species k on the liquid side to species k on the gas side.

where

and where

The usage of the same index, k, on either side of the interface is deliberate and represents a stoichiometric limitation to this type of boundary condition. \(Y_k^l\) and \(Y_k^g\) are the mass fraction of species k on the liquid and gas sides of the interface, respectively. \(W_k^l\) is the molecular weight of species k. \(S_k^l\) is the source term for creation of species k in the liquid phase at the interface (mol \(cm^{-2}\) \(s^{-1}\) ). is the pseudo reaction rate ( \(cm s^{-1}\) ) input from the boundary condition card. \(K_k^c\) is the concentration equilibrium constant, which for the restricted stoichiometry cases covered by this boundary condition, is unitless. \(p_k^v\) is the vapor pressure of gas species k above a liquid entirely consisting of liquid species k. It is a function of temperature. \(\tilde{C}_l\) is the average concentration in the liquid (mol \(cm^{-3}\)). \(C_k^l\) and \(C_k^g\) are the liquid and gas concentrations of species k (mol \(cm^{-3}\)).

The choice for the independent variable is arbitrary, although it does change the actual equation formulation for the residual and Jacobian terms arising from the boundary condition. The internal variable Species_Var_Type in the Uniform_Problem_Description structure may be queried to determine what the actual species independent variable is. Also note, if mole fractions or molar concentration are chosen as the independent variable in the problem, the convention has been to formulate terms of the residuals in units of moles, cm, and seconds. Therefore, division of the equilibrium equations by \(W_k\) would occur before their inclusion into the residual. \(j_k^l\) and \(j_k^g\) are the diffusive flux of species k (gm \(cm^{-2}\) \(s^{-1}\) ) relative to the mass averaged velocity. \(u_s\) is the velocity of the interface. A typical value of \(k^f\) that would lead to good numerical behavior would be 100 cm \(s^{-1}\), equivalent to a reaction with a reactive sticking coefficient of 0.01 at 1 atm and 300 K for a molecule whose molecular weight is near to \(N_2\) or \(H_2S\).

IS_EQUIL_PSEUDORXN¶

BC = IS_EQUIL_PSEUDORXN SS <bc_id> <integer_list> <float>

Description / Usage¶

(WIC/MASS)

This boundary condition card enforces equilibrium between a species component in two ideal solution phases via a finite-rate kinetics formalism. The condition only applies to problems containing internal interfaces with discontinuous (or multilevel) species unknown variables. The species unknown variable must employ the Q1_D or Q2_D interpolation functions in both adjacent element blocks. This boundary condition constrains the species equations on both sides of the interface (i.e., supplies a boundary condition) by specifying the interfacial mass flux on both sides.

IS_EQUIL_PSEUDORXN is equivalent to the VL_EQUIL_PSEUDORXN except for the fact that we do not assume that one side of the interface is a gas and the other is a liquid. Instead, we assume that both materials on either side of the interface are ideal solutions, then proceed to formulate an equilibrium expression consistent with that.

The <integer_list> requires three values; definitions of the input parameters are as follows:

IS_EQUIL_PSEUDORXN	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer1>	Species number.
<integer2>	Element Block ID of the first phase, the “+” phase.
<integer3>	Element Block ID of the second phase, the “-” phase.
<float>	Rate constant for the forward reaction in units of length divided by time.

Examples¶

The sample card:

BC = IS_EQUIL_PSEUDORXN SS 4 0 1 2 100.

demonstrates the following characteristics: species number is “0”; the “+” phase element block id is “1”; the “-” phase element block id is “2”; a forward rate constant of 100. cm \(s^{-1}\).

Technical Discussion¶

The IS_EQUIL_PSEUDORXN boundary condition uses the following equations representing a kinetic approach to equilibrium expressed by an ideal solution model for thermodynamics on either side of the interface. Initially, we relate species k on the + side to species k on the - side of the interface via a kinetic formulation, whose rate constant is fast enough to ensure equilibrium in practice. However, later we may extend the capability to more complicated stoichiometric formulations for equilibrium, since the formulation for the equilibrium expression is readily extensible, unlike Goma’s previous treatment.

where

The “-” phase is defined as the reactants, while the “+” phase is defined to be the products. The expression for the concentration equilibrium constant, \(K_k^c\) , is based on the ideal solution expression for the chemical potentials for species k in the two phases [Denbigh, p. 249],

where \(\mu_k^{+*}\) (T,P) is defined as the chemical potential of species k in its pure state (or a hypothetical pure state if a real pure state doesn’t exist) at temperature T and pressure P. \(\mu_k^{+*}\) (T,P) is related to the standard state of species k in phase +, \(\mu_k^+\), \(\underline{o}\) + (T) , which is independent of pressure, through specification of the pressure dependence of the pure species k. Two pressure dependencies are initially supported:

With these definitions, \(K_k^c\) can be seen to be equal to

where

The chemical potential for a species in a phase will be calculated either from CHEMKIN or from the Chemical Potential, Pure Species Chemical Potential, and Standard State Chemical Potential cards in the materials database file.

The choice for the independent variable for the species unknown is relatively arbitrary,although it does change the actual equation formulation for the residual and Jacobian terms arising from the boundary condition. The internal variable Species_Var_Type in the Uniform_Problem_Description structure is queried to determine what the actual species independent variable is. A choice of SPECIES_UNDEFINED_FORM is unacceptable. If either mole fractions or molar concentration is chosen as the independent variable in the problem, the convention has been to formulate terms of the residuals in units of moles, cm, and seconds. Therefore, division of the equilibrium equations \(W_k\) by occurs before their inclusion into the residual. \(J^l_k\) and \(J^g_k\) are the diffusive flux of species k ( gm \(cm^{-2}\) \(s^{-1}\) ) relative to the mass-averaged velocity. \(u^s\) is the velocity of the interface. A typical value of \(k^f\) that would lead to good numerical behavior would be 100 cm \(s^{-1}\), equivalent to a reaction with a reactive sticking coefficient of 0.01 at 1 atm and 300 K for a molecule whose molecular weight is near to \(N_2\) or \(H_2 S\).

References¶

Denbigh, K., The Principles of Chemical Equilibrium, Cambridge University Press, Cambridge, 1981

SURFACE_CHARGE¶

BC = SURFACE_CHARGE SS <bc_id> <integer> <float>

Description / Usage¶

(SIC/MASS)

The SURFACE_CHARGE card specifies the electrostatic nature of a surface: electrically neutral, positively charged or negatively charged.

Definitions of the input parameters are as follows:

SURFACE_CHARGE	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer>	Index of species to which surface charge condition applies.
<float>	z, value of surface charge.
	0	electroneutrality
	positive z	positively charged surface
	negative z	negatively charged surface

Examples¶

The following input card indicates that on side set 1 species 1 is electrically neutral:

BC = SURFACE_CHARGE SS 1   1   0.0

Category 7: Continuity Equation¶

The continuity equation rarely requires a boundary condition as it represents an overall mass balance constraint on the velocity field for the fluid, viz. normally it is used to enforce incompressibility. Boundary conditions for pressure are most often put on the fluid-momentum equations as a part of the stress condition at an inflow or outflow plane (see for example boundary condition cards FLOW_PRESSURE, FLOW_HYDROSTATIC, etc. ). On occasion, however, we can use a pressure condition as a pressure datum, as the Dirichlet pressure condition below allows, though the user must keep in mind that it is a condition on continuity and not momentum. When using pressure stabilization, viz. PSPG techniques, then also there is an occasional need for a boundary condition on this equation.

P¶

BC = P NS <bc_id> <float1> [float2]

Description / Usage¶

(DC/CONTINUITY)

This Dirichlet boundary condition specification is used to set a constant pressure on a node set. It is generally used for specifying a pressure datum on a single-node node set. The pressure datum is useful for setting the absolute value of the pressure, which, for many problems, is indeterminate to a constant. Pressure datums are especially important for closed flow problems, such as the lid driven cavity, where there is no inflow or outflow. Mass conservation problems can arise if this card is used to specify the pressure along a group of nodes, since this equation replaces the continuity equation. To specify pressure for a group of nodes, it is preferable to use the flow pressure boundary condition, which is applied in a weak sense to the momentum equation and does not cause mass conservation problems. Definitions of the input parameters are as follows:

P	One-character boundary condition name (<bc_name>) that defines the pressure.
NS	Type of boundary condition (<bc_type>), where NS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	Value of pressure.
[float2]	An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

The following are sample cards for specifying a pressure Dirichlet card:

BC = P NS 7   0.

BC = P NS 7   0. 1.0

where the second form is an example using the “residual” method for applying the same Dirichlet condition.

Technical Discussion¶

See the technical discussion for the UVW velocity for a discussion of the two ways of applying Dirichlet boundary conditions.

PSPG¶

BC = PSPG SS <bc_id>

Description / Usage¶

(WIC/CONTINUITY)

This special type of boundary condition exists for pressure-stabilized incompressible flow simulations only. This card should be used only if the value of the Pressure Stabilization card has been set to yes. In conjunction with this feature, equal-order interpolation should be used for the velocity and pressure. If PSPG is used, a boundary integral will be added to the continuity equation to represent the gradients of velocity in the momentum residual, which has been added onto the continuity equation for stabilization. This term is only needed on inflow and outflow boundaries; in the rest of the domain, it cancels out. For more details about the derivation of this term, see the paper by Droux and Hughes (1994).

This boundary condition card requires no integer or floating point constants. Definitions of the input parameters are as follows:

PSPG	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.

Examples¶

The following is an example of using this card on both the inflow and outflow planes of the domain.

BC = PSPG   SS   40

BC = PSPG   SS   20

Technical Discussion¶

Please see Rao (1996) memo for a more detailed discussion of pressure stabilization and its implementation in Goma.

References¶

GTM-001.0: Pressure Stabilization in Goma using Galerkin Least Squares, July 17, 1996, R. R. Rao

Droux, J. J. and T. J. R. Hughes, “A Boundary Integral Modification of the Galerkin Least Squares Formulation for the Stokes Problem, ” Comput. Methods Appl. Mech. Engrg., 113 (1994) 173-182.

PRESSURE DATUM¶

PRESSURE DATUM = <integer> <float>

Description / Usage¶

This card is used to set a hydrodynamic pressure datum on fluid mechanics problems that contain no implicit or explicit boundary conditions on stress or pressure. Definitions of the input parameters are as follows:

<integer>	Element number on which the datum is set. This number should correspond to that shown when viewing the mesh, less one, as the numbering convention in the C language starts at zero rather than at one.
<float>	Value of the hydrodynamic pressure datum.

Noteworthy is that this card is optional, and if used, is placed outside the BC section and just below it.

Examples¶

Following is a sample card:

PRESSURE DATUM = 10 1.

Technical Discussion¶

No Discussion.

Category 8: Porous Equations¶

The following conditions are applied as boundary conditions to the porous-flow equations. These conditions include strong Dirichlet conditions, such as hard sets on porous phase pressure on a boundary as a constant or function of position, weak-form conditions, such as a specified phase flux from a convective mass transfer model or a constant flux, and a host of interfacial conditions for impregnation, etc. The porous flow equations are actually scalar equations that represent component mass balances. Specifically, there is one component mass balance for the liquid phase, one for the gas phase, and one for the solid phase. The corresponding three dependent variables in these balances are the liquid phase pressure, the gas phase pressure, and the porosity, respectively. These variables are related to the flow through a boundary by their normal gradients (Darcy’s law formulation) and to the local inventory of liquid and gas through the saturation function. These implicit terms can often lead to some confusion in setting the boundary conditions so it is recommended that the user consult the supplementary documentation referenced in the following porous boundary condition cards.

POROUS_LIQ_PRESSURE¶

BC = POROUS_LIQ_PRESSURE NS <bc_id> <float1> [float2]

Description / Usage¶

(DC/POR_LIQ_PRES)

This Dirichlet boundary condition is used to set the liquid phase pore pressure at a noden set. It can be applied to a node set on a boundary of a POROUS_SATURATED, POROUS_UNSATURATED or POROUS_TWO_PHASE medium type (see Media Type card).

POROUS_LIQ_PRESSURE	Boundary condition name (bc_name).
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	Value of liquid phase pressure.
[float2]	An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

The boundary condition card

BC = POROUS_LIQ_PRESSURE NS 101 {pcmin}

sets the porous liquid pressure at the boundary denoted by node set 101 to the value represented by the APREPRO variable {pcmin}.

Technical Discussion¶

Setting the porous liquid pressure to a value cannot be done independently of the saturation as the two are related through the vapor pressure curve for simulations in partially saturated media (see Saturation model card). Keep in mind that when using this card in these situations, you are setting also the saturation level based on the capillary pressure, defined as \(p_{gas}\) - \(p_{liq}\) = \(p_c\) . The convention in Goma is that when the capillary pressure \(p_c\) is greater than zero, the saturation level is less than unity, viz. the medium is partially saturated. When \(p_c\) is less than zero, i.e., when the liquid phase pressure is greater than the gas phase pressure, then the medium is saturated (in this case the capillary pressure is poorly defined, though). Also, for Media Type options of POROUS_UNSATURATED, the ambient gas pressure is constant within the pore space and is set by the Porous Gas Constants card in the material file. This boundary condition, when setting the liquid phase pressure, must be used with consideration of these definitions.

For saturated media (viz. Media Type of POROUS_SATURATED), this discussion is not relevant. In this case, one must only consider the pressure level as it may effect the isotropic stress in poroelastic problems.

References¶

GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk

GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk

POROUS_LIQ_FLUX_CONST¶

BC = POROUS_LIQ_FLUX_CONST SS <bc_id> <float1> [float2]

Description / Usage¶

(WIC/POR_LIQ_PRES)

This boundary condition sets the flux of liquid-phase solvent to a constant value in the Galerkin finite element weak sense. Specifically, this flux is applied to a side set as a weak-integrated constant and will set the net flux of liquid phase solvent component (in both gas and liquid phases) to a specified value. It can be applied to material regions of Media Type POROUS_SATURATED, POROUS_UNSATURATED, and POROUS_TWO_PHASE (see Technical Discussion below).

Definitions of the input parameters are as follows:

POROUS_LIQ_FLUX_CONST	Name of boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	Value of the liquid-solvent total flux, in M/ \(L^2\) -t.
[float2]	This optional parameter is not applicable to this boundary condition type, even though it is parsed if present. This parameter is used for boundary conditions of the Dirichlet type.

Examples¶

The input card

BC = POROUS_LIQ_FLUX_CONST SS 102 200.0

sets the total liquid-solvent mass flux, in both gas and liquid phases, to 200.0 along the side set 102.

Technical Discussion¶

This boundary condition is of the mathematical form:

where \(v_s\) is the user supplied convection velocity of the stress-free state as defined on the Convective Lagrangian Velocity card (this is usually zero except in advanced cases), \(p_l^T\) is the total bulk density of liquid phase solvent (in both gas and liquid phase, and hence depends on the local saturation), \(p_l\) is the pure liquid density, \(\phi\) is the porosity, \(p_l\) is the liquid phase pressure, and the other quantities on the second term help define the Darcy velocity. The const quantity is the input parameter identified above (<float1>). Note that this sets the flux relative to the boundary motion to the const value, but by virtue of the Galerkin weak form this condition is automatically applied with const =0 if no boundary condition is applied at the boundary. In a saturated case, viz. POROUS_SATURATED media type, this condition is applied as

References¶

GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk

GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk

POROUS_GAS_PRESSURE¶

BC = POROUS_GAS_PRESSURE NS <bc_id> <float1> [float2]

Description / Usage¶

(DC/POR_GAS_PRES)

This Dirichlet boundary condition is used to set the gas-phase pore pressure at the boundary of a POROUS_TWO_PHASE medium type (see Media Type card). This condition makes no sense on other POROUS Media Types; the gas pressure in those cases is constant and set using the Porous Gas Constants card (Microstructure Properties).

POROUS_GAS_PRESSURE	Boundary condition name (<bc_name>).
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float>	Value of gas phase pressure.
[float2]	An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

The boundary condition card

BC = POROUS_GAS_PRESSURE NS 101 {pgas}

sets the porous gas pressure at the boundary denoted by node set 101 to the value represented by the APREPRO variable {pgas}.

Technical Discussion¶

Setting the porous liquid pressure to a value cannot be done independently of the saturation as the two are related through the vapor pressure curve for simulations in partially saturated media (see Saturation model card). Keep in mind that when using this card in these situations, you are setting also the saturation level based on the capillary pressure, defined as \(p_{gas}\) - \(p_{liq}\) = \(p_c\) . The convention in Goma is that when the capillary pressure \(p_c\) is greater than zero, the saturation level is less than unity, viz.the medium is partially saturated. When \(p_c\) is less than zero, i.e., when the liquid phase pressure is greater than the gas phase pressure, then the medium is saturated (in this case the capillary pressure is poorly defined, though). Also, this pressure sets the datum of pressure for deformable porous media and must be set in a manner compatible with the solid-stress values on the boundaries of the porous matrix.

References¶

GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk

GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk

POROUS_GAS¶

BC = POROUS_GAS SS <bc_id> <integer_list> <float_list>

Description / Usage¶

(SIC/POR_LIQ_PRES)

This boundary condition card is used to equate flux of solvent in the porous medium and external gas. The condition is similar to the solid-liquid interface conditions that apply to interfaces between a porous medium and an external gas (in which the energy equation is used to solve for solvent concentration in the gas phase). This boundary condition is still in development.

There are three values in the <integer_list> and two values in the <float_list> for which to supply values; definitions of the input parameters are as follows:

POROUS_GAS	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer1>	Element block ID of solid, porous phase from the EXODUS II database.
<integer2>	Element block ID of gas phase from the EXODUS II database.
<integer3>	Species number of liquid phase in porous medium.
<float1>	Vapor density.
<float2>	Factor to allow normal velocity in gas.

Examples¶

Users are referred to the Cairncross (1999) reference for the best example of card usage.

Technical Discussion¶

This highly specialized boundary condition is best explained in a paper by Cairncross (1999).

References¶

GTM-028.0: Modeling Drying of Dip-Coated Films with Strongly-Coupled Gas Phase Natural Convection, R. A. Cairncross, 1999.

POROUS_GAS_FLUX_CONST¶

BC = POROUS_GAS_FLUX_CONST SS <bc_id> <float1> [float2]

Description / Usage¶

(WIC/POR_GAS_PRES)

This boundary condition card is used to set the flux of gas-phase solvent to a constant value in the Galerkin finite element weak sense. Specifically, this flux is applied to a side set as a weak-integrated constant and will set the net flux of gas phase solvent component (in both gas and liquid phases, but because the gas solvent is assumed insoluble in the liquid phase, the liquid phase portion vanishes) to a specified value. This boundary condition can be applied to material regions of Media Type POROUS_TWO_PHASE only, as only this type contains a field of gas-phase solvent flux. (See technical discussion below).

Definitions of the input parameters are as follows:

POROUS_GAS_FLUX_CONST	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	Value of the gas-solvent total flux, in M/ \(L^2\) -t.
[float2]	This optional parameter is not applicable to this boundary condition type, even though it is parsed if present. This parameter is used for boundary conditions of the Dirichlet type.

Examples¶

The input card

BC = POROUS_LIQ_FLUX_CONST SS 102 200.0

sets the total gas-solvent mass flux, in the gas phase only, to 200.0 along the side set 102.

Technical Discussion¶

This boundary condition is of the mathematical form:

where \(v_s\) is the user supplied convection velocity of the stress-free state as defined on the Convective Lagrangian Velocity card (this is usually zero except in advanced cases), \(p_g^T\) is the total bulk density of gas phase solvent (in both gas and liquid phase, and hence depends on the local saturation), \(p_g\) is the pure gas density, \(\phi\) is the porosity, \(p_g\) is the gas-phase pressure, and the other quantities on the second term help define the Darcy velocity. The const quantity is the input parameter described above (<float1>). Note that this sets the flux relative to the boundary motion to the const value, but by virtue of the Galerkin weak form this condition is automatically applied with const = 0 if no boundary condition is applied at the boundary.

POROUS_CONV¶

BC = POROUS_CONV SS <bc_id> <integer>

Description / Usage¶

(WIC/POR_LIQ_PRES)

This boundary condition is used to set the total flux of the liquid phase solvent (in both the gas and liquid phase) at the surface of a POROUS_UNSATURATED or POROUS_TWO_PHASE medium to the net convection of solvent due to a superimposed convective Lagrangian velocity (see Media Type card and Convective Lagrangian Velocity card). The only input is an integer indicating which component of the liquid phase solvent is to be set (as of 11/2/01 this component selectability option is not available and as indicated below should be set to zero; this card has not been tested).

Definitions of the input parameters are as follows:

POROUS_CONV	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer>	Species number of transported species. (currently only used for multicomponent species in the phases, which as of 11/2/01 is not active, so set to zero).

Examples¶

Following is a sample card:

BC = POROUS_CONV SS 12 0

that applies a convective flux to side set 12 for porous liquid phase species 0. This species number is currently not used and ignored.

Technical Discussion¶

This boundary condition has the following form

where the left hand side is the total flux of the solvent i in the medium, which includes, in order, the flux due to Darcy flow of gas vapor, the Darcy flow of liquid solvent, the diffusive flux of gas vapor in the pore space and the diffusive flux of liquid solvent in the liquid phase. \(v_s\) is the user supplied convection velocity of the stress-free state as defined on the Convective Lagrangian Velocity card. As of now (11/2/01), this condition is used for a single component liquid solvent and has not been furbished for a single component of that solvent. Also, as of 11/02/01 the condition has not been tested.

References¶

GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk

GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk

POROUS_FLUX¶

BC = POROUS_FLUX SS <bc_id> <integer> <float_list>

Description / Usage¶

(WIC/POR_LIQ_PRES)

This boundary condition is used to set the total flux of the liquid phase solvent (in both the gas and liquid phase) at the surface of a POROUS_UNSATURATED or POROUS_TWO_PHASE medium to mass transfer coefficient times driving force (see Media Type card). The flux quantity is specified on a per mass basis so the mass transfer coefficient is in units of L/t, and the sink density is in units of M/ \(L^3\).

The <float_list> for this boundary condition has four values; the definitions of the input parameters are as follows:

POROUS_FLUX	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer>	Species number of transported species (currently only used for multicomponent species in the phases, which as of 11/2/01 is not active; so set to zero).
<float1>	Value of mass transfer coefficient, \(h_1\) in units of L/t, consistent with gas phase concentration driving force.
<float2>	Driving force concentration in external phase, i.e., sink density, \(p_{gt}^0\) in units of M/ \(L^3\).
<float3>	Value of pressure-driven mass transfer coefficient, \(h_2\) in units of 1/L, for a liquid exiting a partially saturated domain.
<float4>	Driving force concentration in external phase, i.e., sink pressure for liquid extraction, \(p_{liq}^0\) in units of M/L/t.

Examples¶

Following is a sample card:

BC = POROUS_FLUX SS 12 0 0.03 0. 0. 0. 0.

This card applies the lumped mass transfer model for the liquid phase solvent with a mass transfer coefficient of 0.03 and a sink density of 0.0 for the total flux. The boundary condition is applied to side set 12 and to the species number 0. This species number is currently not used and ignored.

Technical Discussion¶

The mathematical form for this boundary condition is as follows

where the left hand side is the total flux of the liquid solvent i in the medium, which includes, in order, the flux due to Darcy flow of gas vapor, the Darcy flow of liquid solvent, the diffusive flux of gas vapor in the pore space and the diffusive flux of liquid solvent in the liquid phase. The parameters are \(h_1\), \(p_g^0\) , \(h_2\) , \(p{liq}^0\) and as defined on the input card. \(v_s\) is the user supplied convection velocity of the stress-free state as defined on the Convective Lagrangian Velocity card.

At the present time (11/2/01), this condition is only used for single component liquid phases and has not been furbished for multicomponent capability yet. Note that usually the second term on the right is turned off, as in the example above, unless the liquid pressure at the surface of the sample is greater than the external pressure. This term was added for applications in which liquid is being squeezed out of a medium and then drips off or disappears, as liquid is not allowed to be sucked back in (Heaviside function, H), although the condition could be furbished for this.

References¶

GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk

GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk

POROUS_PRESSURE¶

BC = POROUS_PRESSURE SS <bc_id> <integer1> <integer2>

Description / Usage¶

(PCC/POR_LIQ_PRES)

This condition enforces a continuous fluid-phase pressure between material types, and is applied to a side set between two materials, one of type POROUS_SATURATED, POROUS_UNSATURATED, or POROUS_TWO_PHASE, and the other of type CONTINUOUS (see material card Media Type). Basically it sets the continuity of hydrodynamic pressure in the continuous fluid to the liquid Darcy pressure in the porous medium, at the interface. The input data is as follows:

POROUS_PRESSURE	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where NS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<integer1>	Element block ID of the porous phase medium.
<integer2>	Element block ID of the continuous fluid phase medium.

Examples¶

An example input card for this boundary condition follows:

BC = POROUS_PRESSURE NS 101   1   2

This card sets the Darcy liquid phase pressure (p_liq in the output EXODUS II file) in element block 1 equal to the continuous phase hydrodynamic pressure (P in the output EXODUS II file) in element block 2.

Technical Discussion¶

The mathematical form for this boundary condition is as follows

but its implementation is not; a memo describing the details of this boundary condition and how it is applied is cited below. This continuity of pressure is critical for the sensitivity of pressurizing the continuos phase to the penetration rate of the porous phase. Interestingly, it forces one to set the pore-phase pressure datum to the same datum in the continuous phase, and that effects the level of the Saturation versus capillary pressure curve (see Saturation material card).

References¶

GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk

GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk

P_LIQ_USER¶

BC = P_LIQ_USER SS <bc_id> <float_list>

Description / Usage¶

(PCC/R_POR_LIQ_PRES)

This boundary condition card is used to call a routine for a user-defined liquid-phase pressure for porous flow problems at an external boundary of a material of one of the following media types: POROUS_SATURATED, POROUS_UNSATURATED, POROUS_TWO_PHASE.. Specification is made via the function p_liq_user_surf in file “user_bc.c.” Definitions of the input parameters are as follows:

P_LIQ_USER	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float_list>	A list of float values separated by spaces which will be passed to the user-defined subroutine so the user can vary the parameters of the boundary condition. This list of float values is passed as a one-dimensional double array to the appropriate C function in file user_bc.c.

Examples¶

The following is a sample input card with two parameters passed to function tuser:

BC =P_LIQ_USER SS 100   273.13 100.0

Technical Discussion¶

No Discussion.

References¶

No References.

POROUS_TEMPERATURE¶

BC = POROUS_TEMPERATURE NS <bc_id> <float1> [float2]

Description / Usage¶

(DC/POR_TEMP)

This Dirichlet boundary condition is used to set the temperature for a nonisothermal porous media problem at a node set. It can be applied to a node set on a boundary of a POROUS_SATURATED, POROUS_UNSATURATED or POROUS_TWO_PHASE medium type (see Media Type card).

POROUS_TEMPERATURE	Boundary condition name (bc_name).
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	Value of temperature at the NS in the porous medium.
[float2]	An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

An example input card for this boundary condition follows:

BC = POROUS_TEMPERATURE NS 101   1.0   1.0

This card sets the temperature(p_temp in the output EXODUS II file) in element block 1 at the nodes defined by nodeset 101. Also, the second 1.0 float is to instruct goma to apply this condition in a residual form.

Technical Discussion¶

This condition is used to set a temperature boundary condition for nonisothermal porous media problems, viz. problems that use the R_POR_ENERGY equation (called EQ = porous_energy). This energy equation is written in multiphase enthalpy form and hence requires a different equatioin that for continuous media.

References¶

GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk

GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk

Category 9: Stress Equations¶

The following conditions provide a means to set boundary conditions for the hyperbolic viscoelastic stress equations

S11¶

BC = {bc_name} NS <bc_id> <float1> [float2]

Description / Usage¶

(DC/STRESS11)

This Dirichlet boundary condition specification is used to set a constant xx-stress for any given mode of the stress tensor. Each such specification is made on a separate input card. Definitions of the input parameters are as follows:

{S11 \| S11_1 \| S11_2 \| S11_3 \| S11_4 \| S11_5 \| S11_6 \| S11_7}	Boundary condition name (<bc_name>) that defines the xx-stress for a given mode, where:
	S11	xx-component of stress tensor for mode 1
	S11_1	xx-component of stress tensor for mode 2
	S11_2	xx-component of stress tensor for mode 3
	S11_3	xx-component of stress tensor for mode 4
	S11_4	xx-component of stress tensor for mode 5
	S11_5	xx-component of stress tensor for mode 6
	S11_6	xx-component of stress tensor for mode 7
	S11_7	xx-component of stress tensor for mode 8
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	Value of xx-stress.
[float2]	An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

Following are sample cards for applying a Dirichlet condition on the xx-stress component for mode 2 on node set 7:

BC = S11_1 NS 7   4.0

BC = S11_1 NS 7   4.0   1.0

where the second example uses the “residual” method for applying the same Dirichlet condition.

Technical Discussion¶

See the technical discussion for the UVW velocity boundary condition for a discussion of the two ways of applying Dirichlet boundary conditions.

For details of the stress tensor and its use for solving viscoelastic flow problems, please see the viscoelastic flow tutorial (Rao, 2000).

References¶

GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao

S12¶

BC = {bc_name} NS <bc_id> <float1> [float2]

Description / Usage¶

(DC/STRESS12)

This Dirichlet boundary condition specification is used to set a constant xy-stress (also known as the shear stress) for any given mode of the stress tensor. Each such specification is made on a separate input card. Definitions of the input parameters are as follows:

{S12 \| S12_1 \| S12_2 \| S12_3 \| S12_4 \| S12_5 \| S12_6 \| S12_7}	Boundary condition name (<bc_name>) that defines the xy-stress for a given mode, where:
	S12	xy-component of stress tensor for mode 1
	S12_1	xy-component of stress tensor for mode 2
	S12_2	xy-component of stress tensor for mode 3
	S12_3	xy-component of stress tensor for mode 4
	S12_4	xy-component of stress tensor for mode 5
	S12_5	xy-component of stress tensor for mode 6
	S12_6	xy-component of stress tensor for mode 7
	S12_7	xy-component of stress tensor for mode 8
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	Value of xy-stress.
[float2]	An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

Following are sample cards for applying a Dirichlet condition on the xy-stress component for mode 5 on node set 10:

BC = S12_4 NS 10   1.25

BC = S12_4 NS 10  1.25   1.0

where the second example uses the “residual” method for applying the same Dirichlet condition.

Technical Discussion¶

See the technical discussion for the UVW velocity boundary condition for a discussion of the two ways of applying Dirichlet boundary conditions.

For details of the stress tensor and its use for solving viscoelastic flow problems, please see the viscoelastic flow tutorial (Rao, 2000).

References¶

GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao

S13¶

BC = {bc_name} NS <bc_id> <float1> [float2]

Description / Usage¶

(DC/STRESS13)

This Dirichlet boundary condition specification is used to set a constant xz-stress for any given mode of the stress tensor. Each such specification is made on a separate input card. Definitions of the input parameters are as follows:

{S13 \| S13_1 \| S13_2 \| S13_3 \| S13_4 \| S13_5 \| S13_6 \| S13_7}	Boundary condition name (<bc_name>) that defines the xz-stress for a given mode, where:
	S13	xz-component of stress tensor for mode 1
	S13_1	xz-component of stress tensor for mode 2
	S13_2	xz-component of stress tensor for mode 3
	S13_3	xz-component of stress tensor for mode 4
	S13_4	xz-component of stress tensor for mode 5
	S13_5	xz-component of stress tensor for mode 6
	S13_6	xz-component of stress tensor for mode 7
	S13_7	xz-component of stress tensor for mode 8
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	Value of xz-stress.
[float2]	An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

Following is a sample card for applying a Dirichlet condition for the xz-stress component for mode 5 on node set 10:

BC = S13_4 NS 10   1.3

BC = S13_4 NS 10   1.3   1.0

where the second example uses the “residual” method for applying the same Dirichlet condition.

Technical Discussion¶

See the technical discussion for the UVW velocity boundary condition for a discussion of the two ways of applying Dirichlet boundary conditions.

For details of the stress tensor and its use for solving viscoelastic flow problems, please see the viscoelastic flow tutorial (Rao, 2000).

References¶

GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao

S22¶

BC = {bc_name} NS <bc_id> <float1> [float2]

Description / Usage¶

(DC/STRESS22)

This Dirichlet boundary condition specification is used to set a constant yy-stress (also known as the shear stress) for any given mode of the stress tensor. Each such specification is made on a separate input card. Definitions of the input parameters are as follows:

{S22 \| S22_1 \| S22_2 \| S22_3 \| S22_4 \| S22_5 \| S22_6 \| S22_7}	Boundary condition name (<bc_name>) that defines the yy-stress for a given mode, where:
	S22	yy-component of stress tensor for mode 1
	S22_1	yy-component of stress tensor for mode 2
	S22_2	yy-component of stress tensor for mode 3
	S22_3	yy-component of stress tensor for mode 4
	S22_4	yy-component of stress tensor for mode 5
	S22_5	yy-component of stress tensor for mode 6
	S22_6	yy-component of stress tensor for mode 7
	S22_7	yy-component of stress tensor for mode 8
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	Value of yy-stress.
[float2]	An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

Following are sample cards for applying a Dirichlet condition on the yy-stress component for mode 8 on node set 20:

BC = S22_7 NS 20   5.0

BC = S22_7 NS 20   5.0   1.0

where the second example uses the “residual” method for applying the same Dirichlet condition.

Technical Discussion¶

See the technical discussion for the UVW velocity boundary condition for a discussion of the two ways of applying Dirichlet boundary conditions.

For details of the stress tensor and its use for solving viscoelastic flow problems, please see the viscoelastic flow tutorial (Rao, 2000).

References¶

GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao

S23¶

BC = {bc_name} NS <bc_id> <float1> [float2]

Description / Usage¶

(DC/STRESS23)

This Dirichlet boundary condition specification is used to set a constant yz-stress for any given mode of the stress tensor. Each such specification is made on a separate input card. Definitions of the input parameters are as follows:

{S23 \| S23_1 \| S23_2 \| S23_3 \| S23_4 \| S23_5 \| S23_6 \| S23_7}	Boundary condition name (<bc_name>) that defines the yz-stress for a given mode, where:
	S23	yz-component of stress tensor for mode 1
	S23_1	yz-component of stress tensor for mode 2
	S23_2	yz-component of stress tensor for mode 3
	S23_3	yz-component of stress tensor for mode 4
	S23_4	yz-component of stress tensor for mode 5
	S23_5	yz-component of stress tensor for mode 6
	S23_6	yz-component of stress tensor for mode 7
	S23_7	yz-component of stress tensor for mode 8
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	Value of yz-stress.
[float2]	An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

Following are sample cards for applying a Dirichlet condition on the yz-stress component for mode 8 on node set 20:

BC = S23_7 NS 20   5.0

BC = S23_7 NS 20   5.0   1.0

where the second example uses the “residual” method for applying the same Dirichlet condition.

Technical Discussion¶

See the technical discussion for the UVW velocity boundary condition for a discussion of the two ways of applying Dirichlet boundary conditions.

For details of the stress tensor and its use for solving viscoelastic flow problems, please see the viscoelastic flow tutorial (Rao, 2000).

References¶

GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao

S33¶

BC = {bc_name} NS <bc_id> <float1> [float2]

Description / Usage¶

(DC/STRESS33)

This Dirichlet boundary condition specification is used to set a constant zz-stress for any given mode of the stress tensor. Each such specification is made on a separate input card. Definitions of the input parameters are as follows:

{S33 \| S33_1 \| S33_2 \| S33_3 \| S33_4 \| S33_5 \| S33_6 \| S33_7}	Boundary condition name (<bc_name>) that defines the zz-stress for a given mode, where:
	S33	zz-component of stress tensor for mode 1
	S33_1	zz-component of stress tensor for mode 2
	S33_2	zz-component of stress tensor for mode 3
	S33_3	zz-component of stress tensor for mode 4
	S33_4	zz-component of stress tensor for mode 5
	S33_5	zz-component of stress tensor for mode 6
	S33_6	zz-component of stress tensor for mode 7
	S33_7	zz-component of stress tensor for mode 8
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	Value of zz-stress.
[float2]	An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

Following are sample cards for applying a Dirichlet condition on the zz-stress component for mode 1 on node set 100:

BC = S33 NS 100   5.0

BC = S33 NS 100   5.0   1.0

where the second example uses the “residual” method for applying the same Dirichlet condition.

Technical Discussion¶

See the technical discussion for the UVW velocity boundary condition for a discussion of the two ways of applying Dirichlet boundary conditions.

For details of the stress tensor and its use for solving viscoelastic flow problems, please see the viscoelastic flow tutorial (Rao, 2000).

References¶

GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao

Category 10: Gradient Equations¶

As companion equations to the viscoelastic stress equations, a continuous velocity gradient is determined through the so-called Velocity Gradient Equations. These boundary conditions are of the Dirichlet type and can be used to put conditions on this class of equations.

G11¶

BC = G11 NS <bc_id> <float1> [float2]

Description / Usage¶

(DC/GRADIENT11)

This Dirichlet boundary condition specification is used to set a constant xx-velocity gradient component of the velocity gradient tensor. Definitions of the input parameters are as follows:

G11	Boundary condition name (<bc_name>) that defines the xx-velocity gradient.
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	Value of xx-velocity gradient.
[float2]	An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

The following is a sample card for applying a Dirichlet condition on the xx-velocity gradient component on node set 100:

BC = G11 NS 100   5.0

BC = G11 NS 100   5.0   1.0

where the second example uses the “residual” method for applying the same Dirichlet condition.

Technical Discussion¶

We solve a simple least squares equation to determine the continuous velocity gradient G from the velocity field. This is done so that we may have a differentiable field to get estimates of the second derivative of the velocity field for applications in complex rheology. The velocity gradient equation is:

Note, that boundary conditions are almost never set on the velocity gradient equation since it is just a least squares interpolation of the discontinuous velocity gradient derived from the velocity field.

See the Technical Discussion for the UVW velocity boundary condition for a discussion of the two ways of applying Dirichlet boundary conditions. For details of the velocity gradient tensor and its use for solving viscoelastic flow problems, please see Rao (2000).

References¶

GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao

G12¶

BC = G12 NS <bc_id> <float1> [float2]

Description / Usage¶

(DC/GRADIENT12)

This Dirichlet boundary condition specification is used to set a constant xy-velocity gradient component of the velocity gradient tensor. Definitions of the input parameters are as follows:

G12	Boundary condition name (<bc_name>) that defines the xy-velocity gradient.
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	Value of xy-velocity gradient.
[float2]	An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

Following is a sample card for applying a Dirichlet condition on the xy-velocity gradient component on node set 100:

BC = G12 NS 100   5.0

BC = G12 NS 100   5.0   1.0

where the second example uses the “residual” method for applying the same Dirichlet condition.

Technical Discussion¶

We solve a simple least squares equation to determine the continuous velocity gradient G from the velocity field. This is done so that we may have a differentiable field to get estimates of the second derivative of the velocity field for applications in complex rheology. The velocity gradient equation is:

Note, that boundary conditions are almost never set on the velocity gradient equation since it is just a least squares interpolation of the discontinuous velocity gradient derived from the velocity field.

See the Technical Discussion for the UVW velocity boundary condition for a discussion of the two ways of applying Dirichlet boundary conditions. For details of the velocity gradient tensor and its use for solving viscoelastic flow problems, please see Rao (2000).

References¶

GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao

G13¶

BC = G13 NS <bc_id> <float1> [float2]

Description / Usage¶

(DC/GRADIENT13)

This Dirichlet boundary condition specification is used to set a constant xz-velocity gradient component of the velocity gradient tensor. Definitions of the input parameters are as follows:

G13	Boundary condition name (<bc_name>) that defines the xz-velocity gradient.
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	Value of xz-velocity gradient.
[float2]	An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

The following is a sample card for applying a Dirichlet condition on the xz-velocity gradient component on node set 100:

BC = G13 NS 100   5.0

BC = G13 NS 100   5.0   1.0

where the second example uses the “residual” method for applying the same Dirichlet condition.

Technical Discussion¶

We solve a simple least squares equation to determine the continuous velocity gradient G from the velocity field. This is done so that we may have a differentiable field to get estimates of the second derivative of the velocity field for applications in complex rheology. The velocity gradient equation is:

Note, that boundary conditions are almost never set on the velocity gradient equation since it is just a least squares interpolation of the discontinuous velocity gradient derived from the velocity field.

See the Technical Discussion for the UVW velocity boundary condition for a discussion of the two ways of applying Dirichlet boundary conditions. For details of the velocity gradient tensor and its use for solving viscoelastic flow problems, please see Rao (2000).

References¶

GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao

G21¶

BC = G21 NS <bc_id> <float1> [float2]

Description / Usage¶

(DC/GRADIENT21)

This Dirichlet boundary condition specification is used to set a constant yx-velocity gradient component of the velocity gradient tensor. Definitions of the input parameters are as follows:

G21	Boundary condition name (<bc_name>) that defines the yx-velocity gradient.
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	Value of yx-velocity gradient.
[float2]	An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

The following is a sample card for applying a Dirichlet condition on the yx-velocity gradient component on node set 100:

BC = G21 NS 100   5.0

BC = G21 NS 100   5.0   1.0

where the second example uses the “residual” method for applying the same Dirichlet condition.

Technical Discussion¶

We solve a simple least squares equation to determine the continuous velocity gradient G from the velocity field. This is done so that we may have a differentiable field to get estimates of the second derivative of the velocity field for applications in complex rheology. The velocity gradient equation is:

Note, that boundary conditions are almost never set on the velocity gradient equation since it is just a least squares interpolation of the discontinuous velocity gradient derived from the velocity field.

See the Technical Discussion for the UVW velocity boundary condition for a discussion of the two ways of applying Dirichlet boundary conditions. For details of the velocity gradient tensor and its use for solving viscoelastic flow problems, please see Rao (2000).

References¶

GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao

G22¶

BC = G22 NS <bc_id> <float1> [float2]

Description / Usage¶

(DC/GRADIENT22)

This Dirichlet boundary condition specification is used to set a constant yy-velocity gradient component of the velocity gradient tensor. Definitions of the input parameters are as follows:

G22	Boundary condition name (<bc_name>) that defines the yy-velocity gradient.
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	Value of yy-velocity gradient.
[float2]	An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

The following is a sample card for applying a Dirichlet condition on the yy-velocity gradient component on node set 100:

BC = G22 NS 100   5.0

BC = G22 NS 100   5.0   1.0

where the second example uses the “residual” method for applying the same Dirichlet condition.

Technical Discussion¶

We solve a simple least squares equation to determine the continuous velocity gradient G from the velocity field. This is done so that we may have a differentiable field to get estimates of the second derivative of the velocity field for applications in complex rheology. The velocity gradient equation is:

Note, that boundary conditions are almost never set on the velocity gradient equation since it is just a least squares interpolation of the discontinuous velocity gradient derived from the velocity field.

See the Technical Discussion for the UVW velocity boundary condition for a discussion of the two ways of applying Dirichlet boundary conditions. For details of the velocity gradient tensor and its use for solving viscoelastic flow problems, please see Rao (2000).

References¶

GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao

G23¶

BC = G23 NS <bc_id> <float1> [float2]

Description / Usage¶

(DC/GRADIENT23)

This Dirichlet boundary condition specification is used to set a constant yz-velocity gradient component of the velocity gradient tensor. Definitions of the input parameters are as follows:

G23	Boundary condition name (<bc_name>) that defines the yz-velocity gradient.
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	Value of yz-velocity gradient.
[float2]	An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

The following is a sample card for applying a Dirichlet condition on the yz-velocity gradient component on node set 100:

BC = G23 NS 100   5.0

BC = G23 NS 100   5.0   1.0

where the second example uses the “residual” method for applying the same Dirichlet condition.

Technical Discussion¶

We solve a simple least squares equation to determine the continuous velocity gradient G from the velocity field. This is done so that we may have a differentiable field to get estimates of the second derivative of the velocity field for applications in complex rheology. The velocity gradient equation is:

Note, that boundary conditions are almost never set on the velocity gradient equation since it is just a least squares interpolation of the discontinuous velocity gradient derived from the velocity field.

See the Technical Discussion for the UVW velocity boundary condition for a discussion of the two ways of applying Dirichlet boundary conditions. For details of the velocity gradient tensor and its use for solving viscoelastic flow problems, please see Rao (2000).

References¶

GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao

G31¶

BC = G31 NS <bc_id> <float1> [float2]

Description / Usage¶

(DC/GRADIENT31)

This Dirichlet boundary condition specification is used to set a constant zx-velocity gradient component of the velocity gradient tensor. Definitions of the input parameters are as follows:

G31	Boundary condition name (<bc_name>) that defines the zx-velocity gradient.
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	Value of zx-velocity gradient.
[float2]	An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

The following is a sample card for applying a Dirichlet condition on the zx-velocity gradient component on node set 100:

BC = G31 NS 100   5.0

BC = G31 NS 100   5.0   1.0

where the second example uses the “residual” method for applying the same Dirichlet condition.

Technical Discussion¶

We solve a simple least squares equation to determine the continuous velocity gradient G from the velocity field. This is done so that we may have a differentiable field to get estimates of the second derivative of the velocity field for applications in complex rheology. The velocity gradient equation is:

Note, that boundary conditions are almost never set on the velocity gradient equation since it is just a least squares interpolation of the discontinuous velocity gradient derived from the velocity field.

See the Technical Discussion for the UVW velocity boundary condition for a discussion of the two ways of applying Dirichlet boundary conditions. For details of the velocity gradient tensor and its use for solving viscoelastic flow problems, please see Rao (2000).

References¶

GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao

G32¶

BC = G32 NS <bc_id> <float1> [float2]

Description / Usage¶

(DC/GRADIENT32)

This Dirichlet boundary condition specification is used to set a constant zy-velocity gradient component of the velocity gradient tensor. Definitions of the input parameters are as follows:

G32	Boundary condition name (<bc_name>) that defines the zy-velocity gradient.
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	Value of zy-velocity gradient.
[float2]	An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

The following is a sample card for applying a Dirichlet condition on the zy-velocity gradient component on node set 100:

BC = G32 NS 100   5.0

BC = G32 NS 100   5.0   1.0

where the second example uses the “residual” method for applying the same Dirichlet condition.

Technical Discussion¶

We solve a simple least squares equation to determine the continuous velocity gradient G from the velocity field. This is done so that we may have a differentiable field to get estimates of the second derivative of the velocity field for applications in complex rheology. The velocity gradient equation is:

Note, that boundary conditions are almost never set on the velocity gradient equation since it is just a least squares interpolation of the discontinuous velocity gradient derived from the velocity field.

See the Technical Discussion for the UVW velocity boundary condition for a discussion of the two ways of applying Dirichlet boundary conditions. For details of the velocity gradient tensor and its use for solving viscoelastic flow problems, please see Rao (2000).

References¶

GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao

G33¶

BC = G33 NS <bc_id> <float1> [float2]

Description / Usage¶

(DC/GRADIENT33)

This Dirichlet boundary condition specification is used to set a constant zz-velocity gradient component of the velocity gradient tensor. Definitions of the input parameters are as follows:

G33	Boundary condition name (<bc_name>) that defines the zz-velocity gradient.
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	Value of zz-velocity gradient.
[float2]	An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

The following is a sample card for applying a Dirichlet condition on the zz-velocity gradient component on node set 100:

BC = G33 NS 100   5.0

BC = G33 NS 100   5.0   1.0

where the second example uses the “residual” method for applying the same Dirichlet condition.

Technical Discussion¶

We solve a simple least squares equation to determine the continuous velocity gradient G from the velocity field. This is done so that we may have a differentiable field to get estimates of the second derivative of the velocity field for applications in complex rheology. The velocity gradient equation is:

Note, that boundary conditions are almost never set on the velocity gradient equation since it is just a least squares interpolation of the discontinuous velocity gradient derived from the velocity field.

See the Technical Discussion for the UVW velocity boundary condition for a discussion of the two ways of applying Dirichlet boundary conditions. For details of the velocity gradient tensor and its use for solving viscoelastic flow problems, please see Rao (2000).

References¶

GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao

Category 11: Shear Rate Equation¶

The single boundary condition in this category is used to set a Dirichlet condition for the scalar shear rate equation. This differential equation is employed by the Phillips model for a suspension constitutive equation.

SH¶

BC = SH NS <bc_id> <float1> [float2]

Description / Usage¶

(DC/SHEAR_RATE)

This boundary condition is used to set a Dirichlet condition for the scalar shear rate unknown field.

Description of the input parameters is as follows:

SH	Name of the boundary condition (<bc_name>).
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	Value at which the scalar shear rate unknown will be fixed on node set <bc_id>.
[float2]	An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

An example of its used:

BC = SH NS 10 0.5

This boundary condition sets the scalar shear rate unknown to 0.5 on nodeset 10.

Technical Discussion¶

The scalar shear rate unknown field is otherwise known as the second invariant of the rate of deformation tensor.

Category 12: Fill Equation¶

The so-called Fill equation is used by the volume-of-fluid and level-set Eulerian interface tracking in Goma. Basically it is a statement of Lagrangian invariance and is hence a hyperbolic statement of the so-called kinematic equation. Given a velocity field, this equation advances the fill function as a set of material points; hence material surfaces remain ostensibly intact. The boundary conditions in this section are used to specify the level-of-fill at a boundary at which a fluid of a specific phase is flowing into the problem domain.

F¶

BC = F NS <bc_id> <float1> [float2]

Description / Usage¶

(DC/FILL)

This Dirichlet boundary condition specifies a value of the fill or level set unknown field on a node set.

A description of the input parameters is as follows:

F	Name of the boundary condition (<bc_name>).
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	Value at which the fill or level set unknown will be fixed on this node set.
[float2]	An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

An example:

BC = F NS 100 1.0

Technical Discussion¶

This boundary condition finds most of its use in the VOF/FILL interface tracking algorithm where it is used to fix the value of the color function at an inlet or outlet boundary. In the level set formulation, it is used less but is still useful in defining the absolute fixed location of an interface by setting the value assigned to 0 on a node set.

FILL_INLET¶

BC = FILL_INLET SS <bc_id> <float1>

Description / Usage¶

(SPECIAL/FILL)

This boundary condition allows the user to specify a value on a inlet boundary from VOF problems employing discontinuous interpolation of the color function, F.

Description of the input parameters is as follows:

FILL_INLET	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	The value of the fill function, F, as it flows across <bc_id> into the domain.

Examples¶

An example:

BC = FILL_INLET SS 10 1.0

Technical Discussion¶

This boundary condition is useful only in problems involving VOF interface tracking in which the fill function is interpolated discontinuously. In this formulation, communication of the fill function value can only be made by finding the value of the fill function in the element upstream of the current position. While this is a stable formulation for the advective VOF method, it does introduce the complexity of determining which element is actually upstream.
When there is no element upstream, as in the case of an inlet boundary, this boundary condition must be present to establish the value of the fill function that is flowing across the inlet boundary into the domain. Consequently, this boundary condition should be present on all inlet boundaries of the problem. It sometimes is also useful to have it on outflow boundaries as well, just in case a backflow situation arises.

Category 13: Potential Equation¶

The Potential equation is a Laplace equation for the voltage (potential) given a charge distribution in a dielectric medium or a voltage or current boundary condition in an electrically conductive medium. The following boundary conditions allow the current or voltage to be set on a boundary.

CURRENT¶

BC = CURRENT SS <bc_id> <float>

Description / Usage¶

(WIC/POTENTIAL)

This card specifies the electrical current density at a given boundary.

Definitions of the input parameters are as follows:

CURRENT	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float>	Value of current density (in A/ \(m^2\) or A/ \(cm^2\), depending on units of length scale used in the problem).

Examples¶

An example input card:

BC = CURRENT SS 1   -0.05

Technical Discussion¶

No Discussion.

CURRENT_USER¶

BC = CURRENT_USER SS <bc_id> <float_list>

Description / Usage¶

(WIC/POTENTIAL)

This boundary condition card is used to define a routine for a user-defined electrical current density model. Definitions of the input parameters are as follows:

CURRENT_USER	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float_list>	A list of float values separated by spaces which will be passed to the user-defined subroutines so the user can vary the parameters of the boundary condition. This list of float values is passed as a one-dimensional double array to the appropriate C function.

Examples¶

The following is a sample input card:

BC = CURRENT_USER SS 100   10.0 3.14159

Technical Discussion¶

No Discussion.

VOLT¶

BC = VOLT NS <bc_id> <float1> [float2]

Description / Usage¶

(DC/POTENTIAL)

This Dirichlet boundary condition card is used to set a constant voltage. Definitions of the input parameters are as follows:

VOLT	Name of the boundary condition (<bc_name>).
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	Value of voltage.
[float2]	An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

Following is a sample card:

BC = VOLT NS 3   -0.22

Technical Discussion¶

No Discussion.

CURRENT_BV¶

BC = CURRENT_BV SS <bc_id> <integer> <floatlist>

Description / Usage¶

(WIC/POTENTIAL)

The CURRENT_BV card enables the specification of variable electrical current density as given by Butler-Volmer kinetics and the Faraday’s law at the specified boundary (namely, an electrode surface).

The <floatlist> has seven parameters for this boundary condition; definitions of the input parameters are as follows:

CURRENT_BV	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer>	Species number of concentration.
<float1>	Stoichiometric coefficient.
<float2>	Kinetic rate constant.
<float3>	Reaction order.
<float4>	Anodic direction transfer coefficient.
<float5>	Cathodic direction transfer coefficient.
<float6>	Electrode potential or applied voltage.
<float7>	Theoretical open-circuit potential.

Examples¶

An example input card:

BC = CURRENT_BV SS 1 0   -1.0 0.000002 1.0 0.21 0.21 -0.65   -0.22

Technical Discussion¶

Users are referred to Chen (2000) for details of the Butler-Volmer model and also Newman (1991), particularly Equations 8.6 and 8.10 and Chapter 8, pp. 188-189 in the latter.

References¶

GTM-025.0: Modeling diffusion and migration transport of charged species in dilute electrolyte solutions: GOMA implementation and sample computed predictions from a case study of electroplating, K. S. Chen, September 21, 2000

1. Newman, “Electrochemical Systems”, Second Edition, Prentice-Hall, Inc. (1991).

CURRENT_HOR¶

BC = CURRENT_HOR SS <bc_id> <integer> <floatlist>

Description / Usage¶

(WIC/POTENTIAL)

The CURRENT_HOR card enables the specification of the variable current density as given by linearized Butler-Volmer kinetics (such as that for the hydrogen-oxidation reaction in polymer-electrolyte-membrane fuel cells) at the specified boundary (i.e., at the electrode surface).

The <floatlist> consists of 9 values; definitions of the input parameters are as follows:

CURRENT_HOR	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer>	Species number of concentration.
<float1>	Product of interfacial area per unit volume by exchange current density, \(ai_0\), in units of A/ \(cm^3\).
<float2>	Catalyst layer or catalyzed electrode thickness, H, in unit of cm.
<float3>	Reference concentration, \(c_{ref}\), in units of moles/ \(cm^3\).
<float4>	Anodic direction transfer coefficient, \(\alpha_a\).
<float5>	Cathodic direction transfer coefficient, \(\alpha_c\).
<float6>	Temperature, T, in unit of K.
<float7>	Theoretical open-circuit potential, \(U_0\), in unit of V.
<float8>	Reaction order, \(\beta\).
<float9>	Electrode potential, V, in unit of V.

Examples¶

The following is a sample input card:

BC = CURRENT_HOR SS 14 0 1000. 0.001 4.e-5 1. 1. 353. 0. 0.5 0.

Technical Discussion¶

For electrochemical reactions such as the hydrogen-oxidation reaction (HOR), surface overpotential is relatively small such that the Butler-Volmer kinetic model can be linearized to yield a simplified equation for computing current density:

where j is current density in units of A/ \(cm^2\); \(ai_0\) denotes the product of interfacial area per unit volume by exchange current density, which has units of A/ \(cm^3\); H is the catalyst layer or catalyzed electrode thickness in unit of cm; c and \(c_{ref}\) are, respectively, species and reference molar concentrations in units of moles/ \(cm^3\); \(\beta\) is reaction order; \(\alpha_a\) and \(\alpha_c\) are, respetively, the anodic and cathodic transfer coefficients; F is the Faraday’s constant ( 96487 C/mole); R is the universal gasl constant ( 8.314 J/mole-K); T is temperature in unit of K; V and \(\phi\) are, respectively, the electrode and electrolyte potentials in unit of V; \(U_0\) and is the open-circuit potential in unit of V.

References¶

Newman, Electrochemical Systems, 2nd Edition, Prentice-Hall, NJ (1991).

K. S. Chen and M. A. Hickner, “Modeling PEM fuel cell performance using the finiteelement method and a fully-coupled implicit solution scheme via Newton’s technique”, in ASME Proceedings of FUELCELL2006-97032 (2006).

CURRENT_ORR¶

BC = CURRENT_ORR SS <bc_id> <integer> <floatlist>

Description / Usage¶

(WIC/POTENTIAL)

The CURRENT_ORR card enables the specification of the variable current density as given by the Tafel kinetics (such as that for the oxygen-reduction reaction in polymerelectrolyte- membrane fuel cells) at the specified boundary (i.e., at the electrode surface).

The <floatlist> consists of 8 values; definitions of the input parameters are as follows:

CURRENT_ORR	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<integer>	Species number of concentration.
<float1>	Product of interfacial area per unit volume by exchange current density, \(ai_0\), in units of A/ \(cm^3\).
<float2>	Catalyst layer or catalyzed electrode thickness, H, in unit of cm.
<float3>	Reference concentration, \(c_{ref}\), in units of moles/ \(cm^3\).
<float4>	Cathodic direction transfer coefficient, \(\alpha_c\).
<float5>	Temperature, T, in unit of K.
<float6>	Electrode potential, V, in unit of V.
<float7>	Theoretical open-circuit potential, \(U_0\), in unit of V.
<float8>	Reaction order, \(\beta\).

Examples¶

The following is a sample input card:

BC = CURRENT_ORR SS 15 1 0.01 0.001 4.e-5 1. 353. 0.7 1.18 1.

Technical Discussion¶

For electrochemical reactions such as the oxygen-reduction reaction (ORR), surface overpotential is large and negative such that the first exponential term in the Butler- Volmer kinetic model is much smaller than the second term and thus can be dropped to yield the Tafel kinetic model for computing current density:

here j is current density in units of A/ \(cm^2\); \(ai_0\) denotes the product of interfacial area per unit volume by exchange current density, which has units of A/ \(cm^3\); H is the catalyst layer or catalyzed electrode thickness in unit of cm; c and \(c_{ref}\) are, respectively, species and reference molar concentrations in units of moles/ \(cm^3\); \(\beta\) is reaction order; \(\alpha_c\) is the anodic and cathodic transfer coefficient; F is the Faraday’s constant ( 96487 C/mole); R is the universal gasl constant ( 8.314 J/mole-K); T is temperature in unit of K; V and \(\phi\) are, respectively, the electrode and electrolyte potentials in unit of V; and \(U_0\) is the open-circuit potential in unit of V.

References¶

Newman, Electrochemical Systems, 2nd Edition, Prentice-Hall, NJ (1991).

K. S. Chen and M. A. Hickner, “Modeling PEM fuel cell performance using the finiteelement method and a fully-coupled implicit solution scheme via Newton’s technique”, in ASME Proceedings of FUELCELL2006-97032 (2006).

VOLT_USER¶

BC = VOLT_USER SS <bc_id> <float_list>

Description / Usage¶

(WIC/POTENTIAL)

This boundary condition card is used to specify a voltage or potential computed via a user-defined function. Definitions of the input parameters are as follows:

VOLT_USER	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float_list>	A list of float values separated by spaces which will be passed to the user-defined subroutines so the user can vary the parameters of the boundary condition. This list of float values is passed as a one-dimensional double array to the appropriate C function.

Examples¶

The following is a sample input card:

BC = VOLT_USER SS 14 0.33 1000. 0.001 4e-5 1. 1. 353. 0.

Technical Discussion¶

In the VOLT_USER model currently implemented in GOMA, the electrolyte potential is given by the linearized Butler-Volmer kinetic model as in the hydrogen-oxidation reaction of a hydrogen-fueled polymer-electrolyte-membrane fuel cell. See the user_bc.c routine for details.

References¶

No References.

Category 14: Fluid-Solid Interaction¶

This is a special group of boundary conditions for problems in which there are two distinct material phases (fluid and solid) with relative motion between them. These BC’s provide a means to apply conditions to a moving boundary with sensitivities to variables in both phases. These problems are formulated in Goma as overset-grid or phase function problems.

LAGRANGE_NO_SLIP¶

BC = LAGRANGE_NO_SLIP SS <bc_id> <integer1> <integer2>

Description / Usage¶

(CONTACT_SURF/R_LAGR_MULT1)

This boundary condition is used to apply a kinematic Lagrange multiplier constraint to a solid/fluid boundary while using Goma’s overset grid capability. The condition is used when the complete fluid-structure interaction problem is being solved, viz. stresses between fluid and solid are both accommodated as is the dynamics of the structure and fluid. In contrast, Goma allows for a structure to be moved through a fluid under prescribed kinematics, and in that case a different Lagrange multiplier constraint is advocated (see LS_NO_SLIP, for example). Two integer inputs together with a sideset ID integer are required for this boundary condition:

LAGRANGE_NO_SLIP	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<integer1>	Element block ID of solid phase from the EXODUS II database.
<integer2>	Element block ID of liquid phase from the EXODUS II database.

Examples¶

Following is a sample card:

BC = LAGRANGE_NO_SLIP SS 2 1 2

In this case the kinematic condition (viz. a velocity match of fluid and solid at the interface) is applied to the interface imprinted by sideset 2. That side set is imprinted on the background fluid mesh. The solid material block ID is 1 in this case and the background fluid material ID is 2.

Technical Discussion¶

In this work, the governing equations consist of a fluid momentum balance:

a mass balance:

and a solid momentum balance:

The kinematic constraint at the fluid-solid interface is:

and the level set function is evaluated at each fluid mesh node by:

The first four equations are written in a Galerkin/Finite form, with \(\phi_i\) representing the weighting functions at node i. The first three equations are enforced at all nodes i that contain the appropriate degrees of freedom (viz. solid or fluid dofs). The fourth equation applies at the solid-liquid interface. \(\rho_f\) and \(\rho_s\) are the fluid and solid material densities, respectively, \(\underline{v}\) is the fluid velocity, \(\underline{F}\) represents any body forces such as gravity, \(\tau\) is the fluid stress tensor, \(\underline{\gamma}\) is the Lagrange multiplier vector unknown, \(\underline{\chi}\) is the solid displacement vector unknown, \(\sigma\) is the solid stress tensor, f is the level set unknown, \(\Theta\) is a step function which is -1 for points within the region occupied by the solid and +1 outside this region, \(\underline{x_i}\) and \(\underline{x_s}\) are the position vectors of a fluid node and of the closest point to it on the solid boundary, respectively, V is the fluid volume domain, S is the solid volume domain, and \(\Gamma\) is the solid boundary (interface) surface domain.

Noteworthy is that this boundary condition applies the second-to-last “kinematic” constraint.

References¶

GT-026.3: Goma’s Overset Mesh Capability. Randy Schunk.

OVERSET_FLUID_SOLID/BAAIJENS_FLUID_SOLID¶

BC = BAAIJENS_FLUID_SOLID PF <pf_id> <integer1> <integer2>

Description / Usage¶

(EMBEDDED_SURF/R_MOMENTUM1)

This boundary condition is used to apply a traction to the fluid that comes from a solid while using Goma’s overset grid capability. The condition is used when the complete fluid-structure interaction problem is being solved, viz. stresses between fluid and solid are both accommodated as is the dynamics of the structure and fluid. The condition is applied to the fluid phase along a zero-level-set contour, hence the PF BC ID type. In another mode of usage, Goma allows for a structure to be moved through a fluid under prescribed kinematics, and in that case this condition is still applied as a solid traction to the fluid. The value of that traction is dictated by the Lagrange multiplier kinematic constraint (cf. LANGRANGE_NO_SLIP BC and LS_NO_SLIP BC). Note that the condition is applied to a boundary in the fluid defined by a phase-field function (see phase1 equation type). . Two integer inputs together with a sideset ID integer are required for this boundary condition:

BAAIJENS_FLUID_SOLD	Name of the boundary condition.
PF	Type of boundary condition (<bc_type>), where PF denotes a surface defined by a phase function (level-set).
<pf_id>	The boundary flag identifier basically sets the number of the phase field function to which this condition applies. For now you must set this to 1, as this phase-field is hardwired to handle the imprinted fluid solid boundary.
<integer1>	Element block ID of solid phase from the EXODUS II database.
<integer2>	Element block ID of liquid phase from the EXODUS II database.

The peculiar name was derived from a paper by Frank Baaijens, from which Goma’s formulation was generated. We are in the process of changing that name to OVERSET_FLUID_SOLID.

Examples¶

Following is a sample card:

BC = BAAIJENS_FLUID_SOLID PF 1 1 2

BC = LS_NO_SLIP PF 1 1 2

This condition set applies a fluid traction condition to a surface defined by phase field 1, which is slaved to a side set that is set in the phase function slave surface capability. (see Phase Function Initialization Method).

Technical Discussion¶

See discussion on LANGRANGE_NO_SLIP. This condition applies the fluid traction boundary term on the fluid momentum equation.

References¶

GT-026.3

OVERSET_SOLID_FLUID/BAAIJENS_SOLID_FLUID¶

BC = OVERSET_SOLID_FLUID SS <bc_id> <float_list>

Description / Usage¶

(CONTACT_SURF/ MESH)

This boundary condition is used to apply a traction to a solid that comes from the fluid while using Goma’s overset grid capability. The condition is used when the complete fluid-structure interaction problem is being solved, viz. stresses between fluid and solid are both accommodated as is the dynamics of the structure and fluid. The condition is applied to the solid phase along a side set that defines the fluid/solid interface. Two integer inputs together with a sideset ID integer are required for this boundary condition:

BAAIJENS_SOLID_FLUID	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<ss_id>	The boundary flag identifier that sets the side set number.
<integer1>	Element block ID of solid phase from the EXODUS II database.
<integer2>	Element block ID of liquid phase from the EXODUS II database.

The peculiar name was derived from a paper by Frank Baaijens, from which Goma’s formulation was generated. We are in the process of changing that name to OVERSET_SOLID_FLUID.

Examples¶

Following is a sample card set:

BC = BAAIJENS_SOLID_FLUID SS 1 2 1

BC = BAAIJENS_FLUID_SOLID PF 1 2 1

BC = LAGRANGE_NO_SLIP SS 1 2 1

Here, the BAAIJENS_SOLID_FLUID cared applies a boundary fluid traction to a solid phase defined by side set 1. In this case the solid phase material ID is 2 and the fluid phase 1.

Technical Discussion¶

See discussion on LAGRANGE_NO_SLIP. Basically, this condition results in a boundary traction set by the Lagrange multiplier constraint to be applied to the solid momentum equation (note the weak term that appears on that equation).

References¶

GT-026.3

F1 F2 F3 F4 F5¶

BC = {F1 | F2 | F3 | F4 | F5} NS <bc_id> <float1> [float2]

Description / Usage¶

(DC/R_PHASE)

This boundary condition format is used to set a constant phase function field values at node sets. Please see “phase#” equation types for a description of the variables. Each such specification (for each field being used) is made on a separate input card. These boundary conditions must be applied to node sets. Definitions of the input parameters are as follows:

{F1 \| F2 \| F3 \| F4 \| F5 }	Two-character boundary condition name (<bc_name>) that defines which phase field variable is being set. There are a maximum of five addtional level-set/phase fields.
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	Value at which the phase field unknown will be fixed on this node set.
[float2]	An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

Following is a sample card which applies an phase field boundary condition to the nodes in node set 100, specifically an phase field-3 value of 1.0.

BC = F3 NS 100 1.0

Technical Discussion¶

This boundary condition finds most of its use in the Phase Function interface tracking algorithm where it is used to fix the value of the color function at an inlet or outlet boundary. The phase function fields were put in to supplement Goma’s base level set capability to provide the ability to model multiple (more than two) materials. We don’t anticipate that these boundary conditions will be used much. Nonetheless, this condition allows Dirichlet conditions to be applied to each of the five additional level set fields.

References¶

GT-026.3

PF_CAPILLARY¶

BC = PF_CAPILLARY LS <integer> <float1> <float2> <float3>

Description / Usage¶

(EMB/VECTOR MOMENTUM)

This boundary condition applies an “embedded” surface tension source term when solving capillary hydrodynamics problems with phase function level set interface tracking. Note that its counterpart for the base level set field is LS_CAPILLARY, and this boundary condition is applied the same way to other level-set fields defined by the Phase Function cards. It can be used with only subgrid integration. The surface tension value used in this boundary condition is obtained from the Surface Tension material parameter defined in the mat file. Note that each phase-function field requires a separate PF_CAPILLARY boundary condition.

A description of the input parameters follows:

PF_CAPILLARY	Name of the boundary condition.
PF	This string is used to indicated that this is a “boundary” condition is applied at an internal phase boundary defined by the zero contour of the level set function.
<integer>	An integer parameter that is used to specify to which phase function field that the boundary condition is to be applied.
<float1>	Not currently used.
<float2>	Not currently used.
<float3>	Not currently used.

Examples¶

An example:

BC = PF_CAPILLARY PF 1

Technical Discussion¶

Surface tension forces at a level set (phase function) representation of an interfacial boundary are applied solely via this boundary condition. An additional divergence of stress tensor term \(\Delta\) ⋅ \(T_{cap}\) is added to the fluid momentum equation. The form of this tensor is

where s is the (isotropic) surface tension, I is the identity tensor, n is the vector normal to the interface and \(\zeta_a\) ( \(\phi\) ) is the smoothed Dirac delta function. The surface tension value used in this expression is obtained from the Surface Tension card found in the material file.

The actual implementation in Goma integrates the divergence term by parts so the expression that is added to the weak form of the momentum equation is:

This fact introduces the issue of integration error into the problem. As obvious above, this source term involves the non-linear Dirac delta function factor. Conventional numerical integration methods often do not offer adequate accuracy in evaluating this integral, especially if if the interface width is a fraction of the average element size. This has led to introduction the level-set-specific integration methods: subelement integration and subgrid integration. In the latter case, more integration points are clustered around the interface (in essence) to improve accuracy. The integer parameter on the card should be set to zero to signify that the surface tension forces are distributed in equal measure on both sides of the interfacial curve.

In the subelement integration case, however, an actual subelement mesh is place on each of the interface-containing elements which is made to conform to the interface curve. That is, the interface curve itself is covered by these subelement boundaries. This allows the volume integral to be collapsed into a line integral and the line integral evaluated along the subelement boundaries. This, however, introduces the problem of identifying which side of the element the surface tension forces should actually be applied to. Applying them to both simultaneously while either result in a cancellation or a doubling of the surface tension effect. For these cases, the integer parameter on this card is set to a -1 or a +1 to signify that the surface tension forces are applied to the negative or positive side of the interface curve, respectively.

References¶

No References.

Category 15: Level Set Interfaces¶

These boundary conditions are designed to apply conditions in materials along surfaces whose position is monitored using Level Set Interface Tracking.

LS_ADC¶

BC = LS_ADC SS <bc_id> <float1> <float2> <float3>

Description / Usage¶

(Special/LEVEL SET)

This boundary condition is used exclusively with level set interface tracking. It is used to simulate contact and dewetting events. It employs a probabilistic model applied to elements on a boundary that contain an interface to determine whether contact or dewetting occurs there. It then uses a direct, brute force algortihm to manipulate the level set field to enforce contact or dewetting.

A description of the input parameters follows:

LS_ADC	Name of the boundary condition.
SS	This string indicates that this boundary is applied to a sideset.
<bc_id>	This is a sideset id where contact or dewetting processes are anticipated. Only elements that border this sideset will be considered as possibilities for ADC events.
<float1>	\(\theta_c\), the capture angle in degrees.
<float2>	\(\alpha_c\), the capture distance (L)
<float3>	\(N_c\), the capture rate ( 1/ \(L^2\) -T)

Examples¶

An example:

BC = LS_ADC SS 10 15.0   0.2   100.0

Technical Discussion¶

It has been found that level set interface tracking problems that involve contact or dewetting of the interfacial representation pose special problems for our numerical method. To a certain extent, we can model this type of event by making special modifications to the slipping properties of the boundary in question, however, this does not always work, especially in the case of dewetting events.

What seems to be the trouble is that we are attempting to use continuum-based models to simulate phenomena that essentially are due to molecular forces being expressed over non-molecular length scales. These length scales, while big with respect to molecules, are small with respect to our problem size. Hence, they are difficult to include in the context of reasonable mesh spacing.

The approach this boundary condition takes to inclusion of contact and dewetting phenomena is not attempt to model the finer details, but to simply note that they are due to “molecular weirdness” and thus take place outside of ordinary continuum mechanics. Therefore, there is some justification for, very briefly and in a localized area, dispensing with continuum mechanics assumption and simply imposing a contact or dewetting event. We refer to these as ADC events and will describe them in more detail later.

The parameters supplied with the card are used to determine where and when such an ADC event occurs. We have chosen to introduce a probabalistic model for this purpose. The reasoning for this comes from reflecting on the dewetting problem. If one imagines a thin sheet of fluid on a wetting substrate, it is clear that dewetting will occur eventually at some point on that sheet. Where that event occurs is somewhat random for a detached perspective. Introduction of a probability model for ADC events attempts to capture this.

Whether an ADC event occurs at an element on the sideset is determined by the following requirements:

The interface surface passes through the element.
There isn’t a contact line in the element.
The angle between the interface normal and the sideset surface normal is less than or equal to the capture angle, \(\theta_c\).
A random number in the range (0,1) determined by the standard C rand() function is less than a probability, P, given by

where d is the average distance of the interface to the sideset in that element, Dt is the time step size, and h is the side length of the element (Note for 2D problems \(h^2\) is replaced by h where the other dimension is assumed unity in the z direction).

Interpretation of this probability relation might take the following course. Given that the fluid interface lies within \(\alpha)c\) of the surface, the length of time necessary before and ADC event is certain to occur is given by 1/ \(N_ch^2\) . Hence, the bigger the capture rate parameter the faster this is likely to occur. The functional form for the case of d > \(\alpha_c\) is included merely to ensure that the probability drops smoothly to zero as quickly as possible. One might point out that the probability at a specific element tends towards zero as the element size decreases. Of course, in that context, the number of elements should increase in number so that the overall probability of an ADC event should not be a function of the degree of mesh refinement. A second point is that this boundary condition can be made to function as means to initiate contact without delay by simply choosing a capture rate that is large enought with respect to the current time step.

Application of an ADC event in a element that meets the preceding criteria is illustrated in the cartoon below:

It is a simple manipulation of the level set values in that element so that the interface will follow the path indicated by the dashed curve in the lower figure. No effort is made in preservation of volume when this is done. The assumption is that these events will occur infrequently enough that this is not a significant problem. However, the user should be aware of this assumption and be careful that these events do not occur on a regular basis as then the mass loss might be more significant.

References¶

No References.

LS_CA_H¶

BC = LS_CA_H SS <bc_id> <float>

Description / Usage¶

(WIC/SCALAR CURVATURE)

This boundary condition is used only in conjunction with level set interface tracking and the LS_CAP_CURVE embedded surface tension source term. Its function is impose a contact angle condition on that boundary.

A description of the input parameters follows:

LS_CA_H	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float>	A float value that is the imposed contact angle in degrees.

Examples¶

An example:

BC = LS_CA_H SS 10 45.0

Technical Discussion¶

The projection equation operator for solving for the curvature degree of freedom from a level set field is a Laplacian. It is standard to integrate these operators by parts but in the process one always generates a boundary integral. In this case the integral takes the form:

where \(n_w\) is the wall surface normal and \(n_{fs}\) is the normal to free surface (zero contour of the level set function ). This is a convenient event because it allows us to impose a contact angle condition on a sideset using this boundary integral by making the assignment

where \(\theta\) is the contact angle specified on the card.

The effect of this boundary condition is impose a disturbance in the curvature field near the boundary that has the effect of accelerating or decelerating the fluid near the wall in response to whether the actual contact angle is greater or less than the imposed value. Thus, over time, given no other outside influences, the contact angle should evolve from its initial value (that presumably is different than the imposed value) to the value imposed on this card. The user should expect that the contact angle will instantaneously jumped to the imposed value.

References¶

No References.

LS_CAPILLARY¶

BC = LS_CAPILLARY LS <integer>

Description / Usage¶

(EMB/VECTOR MOMENTUM)

This boundary condition applies an “embedded” surface tension source term when solving capillary hydrodynamics problems with level set interface tracking. It can be used both when subgrid or subelement integration is being used. The surface tension value used in this boundary condition is obtained from the Surface Tension material parameter defined in the mat file.

A description of the input parameters follows:

LS_CAPILLARY	Name of the boundary condition.
LS	This string is used to indicated that this is a “boundary” condition is applied at an internal phase boundary defined by the zero contour of the level set function.
<integer>	An integer parameter than is permitted to take one of three values -1, 0, or 1. Depending upon the choice of this parameter the surface tension forces are applied to the negative phase, both phase, or the positive phase, respectively. Details are given below.

Examples¶

An example:

BC = LS_CAPILLARY LS 0

Technical Discussion¶

First, a warning: If subelement integration is off, make sure there is a nonzero levelset length scale or no surface forces term will be applied.

Surface tension forces at a level set representation of an interfacial boundary are applied solely via this boundary condition. An additional divergence of stress tensor term \(\Delta\) ⋅ \(T_{cap}\) is added to the fluid momentum equation. Following Jacqmin the form of this tensor is

where s is the (isotropic) surface tension, I is the identity tensor, n is the vector normal to the interface and \(\zeta_a\) ( \(\phi\) ) is the smoothed Dirac delta function. The surface tension value used in this expression is obtained from the Surface Tension card found in the material file.

The actual implementation in Goma integrates the divergence term by parts so the expression that is added to the weak form of the momentum equation is:

This fact introduces the issue of integration error into the problem. As obvious above, this source term involves the non-linear Dirac delta function factor. Conventional numerical integration methods often do not offer adequate accuracy in evaluating this integral, especially if if the interface width is a fraction of the average element size. This has led to introduction the level-set-specific integration methods: subelement integration and subgrid integration. In the latter case, more integration points are clustered around the interface (in essence) to improve accuracy. The integer parameter on the card should be set to zero to signify that the surface tension forces are distributed in equal measure on both sides of the interfacial curve.

In the subelement integration case, however, an actual subelement mesh is place on each of the interface-containing elements which is made to conform to the interface curve. That is, the interface curve itself is covered by these subelement boundaries. This allows the volume integral to be collapsed into a line integral and the line integral evaluated along the subelement boundaries. This, however, introduces the problem of identifying which side of the element the surface tension forces should actually be applied to. Applying them to both simultaneously while either result in a cancellation or a doubling of the surface tension effect. For these cases, the integer parameter on this card is set to a -1 or a +1 to signify that the surface tension forces are applied to the negative or positive side of the interface curve, respectively.

References¶

No References.

LS_FLOW_PRESSURE¶

BC = LS_FLOW_PRESSURE LS <integer> <float1>

Description / Usage¶

(EMB/VECTOR MOMENTUM)

This boundary condition applies a scalar pressure value as an “embedded” source term on the fluid momentum equation at the zero level set contour. It can be used both when subgrid or subelement integration is being used.

A description of the input parameters follows:

LS_FLOW_PRESSURE	Name of the boundary condition.
LS	This string is used to indicated that this is a “boundary” condition is applied at an internal phase boundary defined by the zero contour of the level set function.
<integer>	An integer parameter than is permitted to take one of three values -1, 0, or 1. Depending upon the choice of this parameter the pressure value is applied to the negative phase, both phase, or the positive phase, respectively. Details are given below.
<float1>	P, The constant value of pressure to be applied at the zero level set contour.

Examples¶

An example:

BC = LS_FLOW_PRESSURE LS 0 1013250.0

Technical Discussion¶

This boundary condition is somewhat analogous to the FLOW_PRESSURE boundary condition used quite often in ALE problems. It applies a scalar pressure at the interfacial curve as an embedded boundary condtion. It can be used in by subgrid and subelement methods. In the case of the former, a distributed volume integral of the form:

where \(\vec{n}_{fs}\) is the normal to the level set contour \(\delta_\alpha\) (\(\phi\)) and is the familiar smoothed Dirac delta function with width parameter \(\alpha\). When subelement integration is used this width parameter goes to zero and the volume integral becomes a surface integral along the zero level set contour (Note: as of Oct 2005 subelement integration is not supported for three dimensional problems).

When using this boundary condition concurrent with subgrid integration, the integer parameter that appears on the card should be consistently set to zero. This ensures the volume source will be applied symmetrically. However, when using subelement integration this integer parameter must be entire a +1 or a -1 so that the pressure force will be applied to only on side of the interface and not both which would result in cancellation. This is much the same as was seen for the LS_CAPILLARY boundary condition and the reader is referred to that card for a more detailed discussion.

References¶

No References.

LS_FLUID_SOLID_CONTACT¶

BC = LS_FLUID_SOLID_CONTACT LS <integer> <integer1>

Description / Usage¶

(EMB/MOMENTUM)

This boundary condition applies a fluid-solid stress balance at a level set interface that is slaved to an overset mesh (see GT-026.3). It is applied as an “embedded” source term on the fluid momentum equations at the zero level set contour. NOTE: This boundary condition has been deprecated in favor of the BAAIJENS_SOLID_FLUID and BAAIJENS_FLUID_SOLID boundary conditions, as described in the memo.

A description of the input parameters follows:

LS_FLUID_SOLID_CONTACT	Name of the boundary condition.
LS	This string is used to indicated that this is a “boundary” condition is applied at an internal phase boundary defined by the zero contour of the level set function.
<integer>	An integer parameter than is permitted to take one of three values -1, 0, or 1. Depending upon the choice of this parameter the mass flux value is applied to the negative phase, both phase, or the positive phase, respectively. Details are given below.
<integer1>	Not used. Set to zero.

Technical Discussion¶

We discourage use of this experimental boundary condition.

References¶

No References.

LS_INLET¶

BC = LS_INLET SS <bc_id>

Description / Usage¶

(PCC/LEVEL SET)

This boundary condition is used to set the values of the level set function on a sideset. Most of this is done on an inlet or outlet boundary to elminate the potential for oscillations in the level set field at those points from introducing spurious interfacial (zero contours) .

A description of the input parameters follows:

LS_INLET	Name of the boundary condition.
SS	This string indicates what this boundary is applied to.
<bc_id>	An integer parameter than is permitted to take one of three values -1, 0, or 1. Depending upon the choice of this parameter the surface tension forces are applied to the negative phase, both phase, or the positive phase, respectively. Details are given below.

Examples¶

An example:

BC = LS_INLET SS 10

Technical Discussion¶

Surface tension forces at a level set representation of an interfacial boundary are applied solely via this boundary condition. An additional divergence of stress tensor term \(\Delta\) ⋅ \(T_{cap}\) is added to the fluid momentum equation. Following Jacqmin the form of this tensor is

where s is the (isotropic) surface tension, I is the identity tensor, n is the vector normal to the interface and \(\delta_\alpha\) (\(\phi\)) is the smoothed Dirac delta function. The surface tension value used in this expression is obtained from the Surface Tension card found in the material file.

The actual implementation in Goma integrates the divergence term by parts so the expression that is added to the weak form of the momentum equation is:

This fact introduces the issue of integration error into the problem. As obvious above, this source term involves the non-linear Dirac delta function factor. Conventional numerical integration methods often do not offer adequate accuracy in evaluating this integral, especially if if the interface width is a fraction of the average element size. This has led to introduction the level-set-specific integration methods: subelement integration and subgrid integration. In the latter case, more integration points are clustered around the interface (in essence) to improve accuracy. The integer parameter on the card should be set to zero to signify that the surface tension forces are distributed in equal measure on both sides of the interfacial curve.

In the subelement integration case, however, an actual subelement mesh is place on each of the interface-containing elements which is made to conform to the interface curve. That is, the interface curve itself is covered by these subelement boundaries. This allows the volume integral to be collapsed into a line integral and the line integral evaluated along the subelement boundaries. This, however, introduces the problem of identifying which side of the element the surface tension forces should actually be applied to. Applying them to both simultaneously while either result in a cancellation or a doubling of the surface tension effect. For these cases, the integer parameter on this card is set to a -1 or a +1 to signify that the surface tension forces are applied to the negative or positive side of the interface curve, respectively.

References¶

No References.

LS_NO_SLIP¶

BC = LS_NO_SLIP PF <integer>

Description / Usage¶

(EMB/VECTOR MOMENTUM)

This boundary condition is used to enforce the fluid/solid kinematic constraint for 1) overset grid applications in which 2) the solid material is assumed rigid and therefore has no internal stresses. It requires 3) a slaved phase function be defined along with 4) a vector field of Lagrange multipliers.

A description of the input parameters follows:

LS_NO_SLIP	Name of the boundary condition.
PF	This string indicates that this boundary condition is going to be applied along the zero contour of an embedded phase function (PF) field.
<integer>	This integer identifies the specific phase function field that is defining the contour. At the present time this integer should always be one.

Examples¶

An example:

BC = LS_NO_SLIP PF 1

Technical Discussion¶

This boundary condition is used in the context of Goma’s overset grid capability. A thorough treatment of this method is provided in the Goma document (GT-026.3) and the user is directed there. However, a brief discussion of the nature of this boundary condition is in order at this point.

The overset grid capability is used in problems in which a solid material is passing through a fluid material. The solid and fluid materials both have there own meshes. In the general problem, stresses and velocities must be transferred between each phase and therefore there is two-coupling of the respective momentum and continuity equations. This boundary condition, however, is used in the restricted case in which the solid material is assumed to be rigid and having a prescribed motion. Therefore, the coupling only proceeds in one direction : solid to fluid.

This boundary condition concerns itself with enforcing the kinematic constraint:

between the solid material with prescribed motion, \(\underline {\dot{x}}\) , and the fluid whose velocity is, \(\gamma\). This kinematic constraint represents a new set of equations in the model for which unknowns must be associated. In this case, we introduce a Lagrange multiplier vector field, \(\underline{\gamma}\) , at each node in the mesh. For fluid elements that do not intersect the fluid/ solid interface, these Lagrange multipliers are identically zero. They are non zero only for those fluid elements that are crossed by the fluid/solid boundary. These Lagrange multiplier fields couple the influence of the solid material on the fluid through body force terms in the fluid momentum equations of the form:

When applying this boundary condition it is necessary to include Lagrange multiplier equations equal to the number of dimensions in the problem. These are specified in the equation section of the input deck. The shape and weight functions for these fields are generally simple P0 functions. If one were to vector plot the components of the Lagrange multiplier components, you get a general picture of the force interaction field between the liquid and solid. This is sometimes informative.

A slaved phase function field is used to imprint the contour of the solid material on the liquid mesh. The zero contour of this function is then used to evaluate the above line integral. This phase function field is slaved to the solid material and is not evolved in the conventional sense. Nonetheless, a single phase function field equation must be included with the set of equations solved. In the phase function parameters section of the input deck, the user must indicate that this phase function is slaved and also must identify the sideset number of the boundary on the solid material which is the fluid/ solid interface.

References¶

No References.

LS_Q¶

BC = LS_Q LS <integer> <float1>

Description / Usage¶

(EMB/ENERGY)

This boundary condition applies a scalar heat flux value as an “embedded” source term on the heat conservation equation at the zero level set contour. It can be used both when subgrid or subelement integration is being used.

A description of the input parameters follows:

LS_Q	Name of the boundary condition.
LS	This string is used to indicated that this is a “boundary” condition is applied at an internal phase boundary defined by the zero contour of the level set function.
<integer>	An integer parameter than is permitted to take one of three values -1, 0, or 1. Depending upon the choice of this parameter the heat flux value is applied to the negative phase, both phase, or the positive phase, respectively. Details are given below.
<float1>	q, The constant value of heat flux to be applied at the zero level set contour.

Examples¶

An example:

BC = LS_Q LS 0 -1.1e-3

Technical Discussion¶

This boundary condition is somewhat analogous to the QSIDE boundary condition used quite often in non-level set problems. It applies a scalar heat flux at the interfacial curve as an embedded boundary condtion. It can be used in by subgrid and subelement methods. In the case of the former, a distributed volume integral of the form:

where \(\Delta\) ⋅ \(T_{cap}\) is the familiar smoothed Dirac delta function with width parameter \(\alpha\). When subelement integration is used this width parameter goes to zero and the volume integral becomes a surface integral along the zero level set contour (Note: as of Oct 2005 subelement integration is not supported for three dimensional problems).

When using this boundary condition concurrent with subgrid integration, the integer parameter that appears on the card should be consistently set to zero. This ensures the volume source will be applied symmetrically. However, when using subelement integration this integer parameter must be entire a +1 or a -1 so that the heat flux will be applied only on side of the interface and not both which would result in cancellation. This is much the same as was seen for the LS_CAPILLARY boundary condition and the reader is referred to that card for a more detailed discussion.

References¶

No References.

LS_QRAD¶

BC = LS_QRAD LS <integer> <float1> <float2> <float3> <float4>

Description / Usage¶

(EMB/ENERGY)

This boundary condition card specifies heat flux using both convective and radiative terms. This heat flux value is applied as an “embedded” source term on the heat conservation equation at the zero level set contour (cf. BC = QRAD for ALE surfaces). It can be used both when subgrid or subelement integration is being used. The <float_list> has four parameters; definitions of the input parameters are as follows:

A description of the input parameters follows:

LS_QRAD	Name of the boundary condition.
LS	This string is used to indicated that this is a “boundary” condition is applied at an internal phase boundary defined by the zero contour of the level set function.
<integer>	An integer parameter than is permitted to take one of three values -1, 0, or 1. Depending upon the choice of this parameter the heat flux value is applied to the negative phase, both phase, or the positive phase, respectively. Details are given below.
<float1>	h, convective heat transfer coefficient.
<float2>	\(T_s\), sink temperature.
<float3>	\(\varepsilon\), total hemispherical emissivity.
<float4>	\(\sigma\), Stefan-Boltzmann constant.

Examples¶

An example:

BC = LS_QRAD LS 0 10.0 273.0 0.3 5.6697e-8

Technical Discussion¶

This is the level-set counterpart to BC = QRAD which is the same boundary condition applied to a parameterized mesh surface. Please see the discussion of that input record for the functional form of this boundary condition.

References¶

No References.

LS_QLASER¶

BC = LS_QLASER LS <integer> <float1> <float2> <float3> <float4>

Description / Usage¶

(EMB/ENERGY)

This boundary condition card specifies heat flux model derived from a laser welding application. This heat flux value is applied as an “embedded” source term on the heat conservation equation at the zero level set contour (cf. BC = Q_LASER_WELD for ALE surfaces). It can be used both when subgrid or subelement integration is being used. The <float_list> has twenty-seven parameters; definitions of the input parameters are as follows:

A description of the input parameters follows:

LS_QLASER	Name of the boundary condition.
LS	This string is used to indicated that this is a “boundary” condition is applied at an internal phase boundary defined by the zero contour of the level set function.
<integer>	An integer parameter than is permitted to take one of three values -1, 0, or 1. Depending upon the choice of this parameter the heat flux value is applied to the negative phase, both phase, or the positive phase, respectively. Details are given below.
<float 1>	Nominal power of laser.
<float 2>	Power of laser at base state (simmer).
<float 3>	Base value of surface absorptivity.
<float 4>	Switch to allow tracking of normal component of liquid surface relative to laser beam axis for surface absorption (0 = OFF, 1 = ON)
<float 5>	Cutoff time for laser power.
<float 6>	Time at which laser power drops to 1/e.
<float 7>	For pulse weld, the laser power overshoot (%) of peak power at time to reach peak laser power.
<float 8>	Radius of laser beam.
<float 9>	For pulse weld, the time for laser pulse to reach peak power.
<float 10>	For pulse weld, the time for laser pulse to reach steady state in power.
<float 11>	Switch to either activate laser power distribution from beam center based on absolute distance (0) or based on radial distance in 2D plane (1).
<float 12>	Location of laser beam center (x-coordinate).
<float 13>	Location of laser beam center (y-coordinate).
<float 14>	Location of laser beam center (z-coordinate).
<float 15>	Laser beam orientation, normal to x-coordinate of body.
<float 16>	Laser beam orientation, normal to y-coordinate of body.
<float 17>	Laser beam orientation, normal to z-coordinate of body.
<float 18>	For pulse weld, spot frequency.
<float 19>	For pulse weld, total number of spots to simulate.
<float 20>	Switch to set type of weld simulation. (0=pulse weld, 1=linear continuous weld, -1=pseudo pulse weld, 2=sinusoidal continous weld)
<float 21>	For pulse weld, spacing of spots.
<float 22>	For radial traverse continuous weld, radius of beam travel.
<float 23>	Switch to activate beam shadowing for lap weld (0=OFF, 1=ON). Currently only active for ALE simulations.
<float 24>	Not active, should be set to zero.
<float 25>	For continuous weld, laser beam travel speed in xdirection (u velocity).
<float 26>	For continuous weld, laser beam travel speed in ydirection (v velocity).
<float 27>	For continuous weld, laser beam travel speed in zdirection (w velocity).

Examples¶

An example:

BC = LS_QLASER LS -1 4.774648293 0 0.4 1 1 1.01 4.774648293 0.2
0.01 0.01 1 0.005 0 -0.198 -1 0 0 0.025 1 1 0.2032 -1000 0 0 0 0
0.0254

Technical Discussion¶

This is the level-set counterpart to BC = Q_LASER which is the same boundary condition applied to a parameterized mesh surface. Please see the discussion of that input record for the functional form of this boundary condition.

References¶

No References.

LS_RECOIL_PRESSURE¶

BC = LS_RECOIL_PRESSURE LS <integer> <float1> <float2> <float3> <float4>

Description / Usage¶

(EMB/VECTOR MOMENTUM)

This boundary condition card specifies heat flux model derived from a laser welding application.. This heat flux value is applied as an “embedded” source term on the heat conservation equation at the zero level set contour (cf. BC = CAP_RECOIL_PRESS for ALE surfaces). It can be used both when subgrid or subelement integration is being used. The <float_list> has seven parameters; definitions of the input parameters are as follows:

A description of the input parameters follows:

LS_RECOIL_PRESSURE	Name of the boundary condition.
LS	This string is used to indicated that this is a “boundary” condition is applied at an internal phase boundary defined by the zero contour of the level set function.
<integer>	An integer parameter than is permitted to take one of three values -1, 0, or 1. Depending upon the choice of this parameter the heat flux value is applied to the negative phase, both phase, or the positive phase, respectively. Details are given below.
<float1>	This float is currently disabled.
<float2>	This float is currently disabled.
<float3>	This float is currently disabled.
<float4>	Disabled. The boiling temperature is set to the melting point of the solidus. Use the material property “Solidus Temperature” card for this.
<float5>	This float is currently disabled.
<float6>	Conversion scale for pressure.
<float7>	Conversion scale for temperature.

Examples¶

Technical Discussion¶

Currently this boundary condition has coefficients for only iron and water. Several required pieces of information to use this boundary condition are not in final form, and the user can expect future changes and improvements. This boundary condition is designed for use with LS_QLASER.

References¶

No References.

LS_VAPOR/LS_QVAPOR¶

BC = LS_VAPOR LS <integer> <float1> <float2> <float3> <float4>

Description / Usage¶

(EMB/ENERGY)

This boundary condition card specifies heat flux model derived from a laser welding application. This particular contribution accounts for the energy lost by vapor flux. This heat flux value is applied as an “embedded” source term on the heat conservation equation at the zero level set contour (cf. BC = Q_LASER_WELD for ALE surfaces). It can be used both when subgrid or subelement integration is being used. The <float_list> has four parameters; definitions of the input parameters are as follows:

A description of the input parameters follows:

LS_VAPOR	Name of the boundary condition.
LS	This string is used to indicated that this is a “boundary” condition is applied at an internal phase boundary defined by the zero contour of the level set function.
<integer>	An integer parameter than is permitted to take one of three values -1, 0, or 1. Depending upon the choice of this parameter the heat flux value is applied to the negative phase, both phase, or the positive phase, respectively. Details are given below.
<float1>	T_scale. Temperature scaling.
<float2>	q_scale. Heat flux scaling.

Examples¶

An example:

BC = LS_VAPOR LS 0 273. 1.

Technical Discussion¶

Currently this BC is hardwired to parameters (viz. heat capacitance, etc.) for iron. The melting point temperature is taken from the material property “Liquidus Temperature”. This boundary condition is still in the developmental stage. In using it is advisable to be working with the Sandia Goma code team.

References¶

No References.

LS_YFLUX¶

BC = LS_YFLUX LS <integer> <integer1> <float1> <float2>

Description / Usage¶

(EMB/ENERGY)

This boundary condition applies a scalar mass flux value as an “embedded” source term on a species conservation equation at the zero level set contour. It can be used both when subgrid or subelement integration is being used.

A description of the input parameters follows:

LS_YFLUX	Name of the boundary condition.
LS	This string is used to indicated that this is a “boundary” condition is applied at an internal phase boundary defined by the zero contour of the level set function.
<integer>	An integer parameter than is permitted to take one of three values -1, 0, or 1. Depending upon the choice of this parameter the mass flux value is applied to the negative phase, both phase, or the positive phase, respectively. Details are given below.
<integer1>	w, This the species equation index to which this boundary condition is applied.
<float1>	\(h_c\), a constant value for the mass transfer coefficient at the interface.
<float2>	\(Y_c\), the “bulk” concentration of species used in conjunction with the mass transfer coefficient to compute the mass flux.

Examples¶

An example:

BC = LS_YFLUX LS 0 0 1.e-2 0.75

Technical Discussion¶

This boundary condition is somewhat analogous to the YFLUX boundary condition used quite often in non-level set problems to apply a scalar species flux at a at boundary defined by a side set. It applies a scalar mass transfer flux at the interfacial curve as an embedded boundary condtion. It can be used in by subgrid and subelement methods. In the case of the former, a distributed volume integral of the form:

where \(\delta_\alpha\) (\(\phi\)) is the familiar smoothed Dirac delta function with width parameter \(\alpha\) and the mass flux , J, is given by the typical relation:

When subelement integration is used this width parameter goes to zero and the volume integral becomes a surface integral along the zero level set contour (Note: as of Oct 2005 subelement integration is not supported for three dimensional problems).

When using this boundary condition concurrent with subgrid integration, the integer parameter that appears on the card should be consistently set to zero. This ensures the volume source will be applied symmetrically. However, when using subelement integration this integer parameter must be entire a +1 or a -1 so that the mass flux will be applied only on side of the interface and not both which would result in cancellation. This is much the same as was seen for the LS_CAPILLARY boundary condition and the reader is referred to that card for a more detailed discussion.

References¶

No References.

SHARP_BLAKE_VELOCITY¶

BC = SHARP_BLAKE_VELOCITY SS <bc_id> <floatlist

Description / Usage¶

(WIC/VECTOR MOMENTUM)

This boundary condition is used to induce fluid velocity at a wetting line when using Level Set Interface Tracking. Its formulation is identical to the WETTING_SPEED_BLAKE boundary condition, but it is applied as a single point source on the boundary instead of a distributed stress.

This boundary condition can only be used for two-dimensional problems.

A description of the input parameters follows:

SHARP_BLAKE_VELOCITY	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	\(\theta_s\), the static contact angle in degress.
<float2>	V_0 is a pre-exponential velocity factor (see functional form below).
<float3>	g is a thermally scaled surface tension, i.e. \(\sigma\) /2nkT.
<float4>	\(\beta\), slip coefficient.
<float5>	\(t_{relax}\) is a relaxation time which can be used to smooth the imposed contact point velocity for transient problems. Set to zero for no smoothing.
<float6>	\(V_{old}\) is an initial velocity used in velocity smoothing for transient problems. Set to zero when smoothing is not used.

Examples¶

An example:

BC = SHARP_BLAKE_VELOCITY SS 10 30.0 0.1 8. 0.001 0   0

Technical Discussion¶

The implementation for this wetting condition is identical to that of SHARP_WETLIN_VELOCITY, but the wetting velocity dependence is different. Because the wetting stress is not applied at a point, it is most appropriate for use when using subelement integration which similarly collapses the surface tension sources associated with the interface onto the interfacial curve.

Note also that this boundary condition is strictly for use with two-dimensional problems. Attempting to apply it to a three dimensional problem will result in an error message.

Theory¶

Derivation of the force condition for this boundary condition starts with a simple relation for wetting line velocity

Note that the convention for contact angles in this relation is that values of θ near to zero indicate a high degree of wetting and values of θ near 180 ° indicate the opposite. This is mapped to a stress value by analogy with Navier’s slip relation and has the following form when the velocity smoothing is not used,

References¶

No References.

SHARP_CA_2D¶

BC = SHARP_CA_2D SS <bc_id> <float>

Description / Usage¶

(WIC/VECTOR MOMENTUM)

This boundary condition is used to impose a contact angle on a boundary when using Level Set Interface Tracking. It can only be used for two-dimensional problems.

A description of the input parameters follows:

FILL_CA	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float>	\(\theta\), the contact angle imposed, in degrees.

Examples¶

An example:

BC = SHARP_CA_2D SS 10 30.0

Technical Discussion¶

This boundary condition must be used in conjunction with the VELO_SLIP_FILL or VELO_SLIP_LS boundary condition. These latter conditions permits the fluid to slip in the vicinity of the contact line. The SHARP_CA_2D acts by imposing a force on the momentum equation. The size of this force is more or less in proportion between the actual contact angle on the boundary and the value specified on the card and scales directly with the applied surface tension material parameter. In this manner, it is very similar to the FILL_CA boundary condition.

The manner in which is applied differs. In this case, the applied force is not distributed around the contact line using a smooth delta function weighting in a weak integrated context, but instead the delta function is used to resolve the line integral and the force is applied directly at a point on the sideset set. Hence, this boundary condition is most appropriate for use in conjunction with subelement integration which performs a similar transformation of the volumetric surface tension source terms. Further, the logic use to identify the point of application on the boundary functions only in twodimensions. Hence, this boundary condition is stricly limited to two-dimensional problems.

References¶

No References.

SHARP_COX_VELOCITY¶

BC = SHARP_COX_VELOCITY SS <bc_id> <floatlist

Description / Usage¶

(WIC/VECTOR MOMENTUM)

This boundary condition is used to induce fluid velocity at a wetting line when using Level Set Interface Tracking. Its formulation is identical to the WETTING_SPEED_COX boundary condition, but it is applied as a single point source on the boundary instead of a distributed stress.

This boundary condition can only be used for two-dimensional problems.

A description of the input parameters follows:

SHARP_COX_VELOCITY	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	\(\theta_s\), the static contact angle in degress.
<float2>	\(\sigma\) is the surface tension.
<float3>	\(\varepsilon_s\) is the dimensionless slip length, i.e. the ratio of the slip length to the characteristic length scale of the macroscopic flow.
<float4>	\(\beta\), slip coefficient.
<float5>	\(t_{relax}\) is a relaxation time which can be used to smooth the imposed contact point velocity for transient problems. Set to zero for no smoothing.
<float6>	\(V_{old}\) is an initial velocity used in velocity smoothing for transient problems. Set to zero when smoothing is not used.

Examples¶

An example:

BC = SHARP_COX_VELOCITY SS 10 30.0 72.0 0.01 0.1   0   0

Technical Discussion¶

The implementation for this wetting condition is identical to that of SHARP_WETLIN_VELOCITY, but the wetting velocity dependence is different. Because the wetting stress is not applied at a point, it is most appropriate for use when using subelement integration which similarly collapses the surface tension sources associated with the interface onto the interfacial curve.

Note also that this boundary condition is strictly for use with two-dimensional problems. Attempting to apply it to a three dimensional problem will result in an error message.

Theory¶

Derivation of the force condition for this boundary condition starts with a relation for wetting line velocity

where \(V_{Cox}\) is computed from the Cox hydrodynamic wetting theory;

See VELO_THETA_COX for details of the Cox functions f and g. Note that the parameters \(\lambda\), \(q_{inner}\), and \(q_{outer}\) are currently not accessible from the input card and are hard-set to zero. \(\lambda\) is the ratio of gas viscosity to liquid viscosity whereas \(q_{inner}\) and \(q_{outer}\) represent influences from the inner and outer flow regions.

Note that the convention for contact angles in this relation is that values of θ near to zero indicate a high degree of wetting and values of \(\theta\) near 180 ° indicate the opposite. This is mapped to a stress value by analogy with Navier’s slip relation and has the following form when the velocity smoothing is not used,

The Cox wetting velocity requires evaluation of integrals for the function g(\(\theta\), \(\lambda\)) which is currently done numerically using 10-point Gaussian quadrature. As such the evaluation of the integrals is expected to become inaccurate as either \(\theta_s\) tends toward zero or \(\theta\) tends toward 180 degrees. Note that the integrand becomes singular as \(\theta\) tends toward 0 or 180 degrees.

References¶

No References.

SHARP_HOFFMAN_VELOCITY¶

BC = SHARP_HOFFMAN_VELOCITY SS <bc_id> <floatlist

Description / Usage¶

(WIC/VECTOR MOMENTUM)

This boundary condition is used to induce fluid velocity at a wetting line when using Level Set Interface Tracking. Its formulation is identical to the WETTING_SPEED_HOFFMAN boundary condition, but it is applied as a single point source on the boundary instead of a distributed stress.

This boundary condition can only be used for two-dimensional problems.

A description of the input parameters follows:

SHARP_HOFFMAN_VELOCITY	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	\(\theta_s\), the static contact angle in degress.
<float2>	\(\sigma\) is the surface tension.
<float3>	\(\beta\), slip coefficient.
<float4>	\(t_{relax}\) is a relaxation time which can be used to smooth the imposed contact point velocity for transient problems. Set to zero for no smoothing.
<float5>	\(V_{old}\) is an initial velocity used in velocity smoothing for transient problems. Set to zero when smoothing is not used.

Examples¶

An example:

BC = SHARP_HOFFMAN_VELOCITY SS 10 30.0 72.0 0.1   0   0

Technical Discussion¶

The implementation for this wetting condition is identical to that of SHARP_WETLIN_VELOCITY, but the wetting velocity dependence is different. Because the wetting stress is not applied at a point, it is most appropriate for use when using subelement integration which similarly collapses the surface tension sources associated with the interface onto the interfacial curve.

Note also that this boundary condition is strictly for use with two-dimensional problems. Attempting to apply it to a three dimensional problem will result in an error message.

Theory¶

Derivation of the force condition for this boundary condition starts with a relation for wetting line velocity

where \(V_{Hoffman}\) is computed from the Hoffman correlation;

See VELO_THETA_HOFFMAN for details of the Hoffman function g. Note that the convention for contact angles in this relation is that values of \(\theta\) near to zero indicate a high degree of wetting and values of \(\theta\) near 180 ° indicate the opposite. This is mapped to a stress value by analogy with Navier’s slip relation and has the following form when the velocity smoothing is not used,

Because the Hoffman functions are implicit, iteration is required in the determination of the wetting velocity. As a result, for very high Capillary numbers, i.e. > \(10^6\), the iteration procedure in Goma may need to be modified.

References¶

No References.

SHARP_WETLIN_VELOCITY¶

BC = SHARP_WETLIN_VELOCITY SS <bc_id> <floatlist

Description / Usage¶

(WIC/VECTOR MOMENTUM)

This boundary condition is used to induce fluid velocity at a wetting line when using Level Set Interface Tracking. Its formulation is identical to the WETTING_SPEED_LINEAR boundary condition, but it is applied as a single point source on the boundary instead of a distributed stress.

This boundary condition can only be used for two-dimensional problems.

A description of the input parameters follows:

SHARP_WETLIN_VELOCITY	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	\(\theta_s\), the static contact angle in degress.
<float2>	\(c_T\), proportionality constant as defined below
<float3>	Currently not used.
<float4>	\(\beta\), slip coefficient.

Examples¶

An example:

BC = SHARP_WETLIN_VELOCITY SS 10 30.0 0.1 0. 0.001

Technical Discussion¶

As noted above, this boundary condition imposes the same wetting stress dependence as the WETTING_SPEED_LINEAR boundary condition. However, its application in the FEM context is different. Instead of the wetting stress, \(\tau_w\), being applied according to the formula:

as is the case for the WETTING_SPEED_LINEAR condition, the Dirac function is used to remove the integral and replace it with a point stress at the location where \(\phi\) = 0 on the boundary. Designating this point as \(X_{cl}\), the vector applied to the momentum equation is given by

Because the wetting stress is not applied at a point, it is most appropriate for use when using subelement integration which similarly collapses the surface tension sources associated with the interface onto the interfacial curve. Note that this method of application is identical to the SHARP_CA_2D boundary condition discussed elsewhere.

Note also that this boundary condition is strictly for use with two-dimensional problems. Attempting to apply it to a three dimensional problem will result in an error message.

Theory¶

Derivation of the force condition for this boundary condition starts with a simple relation for wetting line velocity

Note that the convention for contact angles in this relation is that values of \(\theta\) near to zero indicate a high degree of wetting and values of \(\theta\) near 180 ° indicate the opposite. This is mapped to a stress value by analogy with Navier’s slip relation,

It should be noted that there is no distinction for this model in the function of \(\beta\) or \(c_T\). The two parameters are interchangeable. In non-linear models, (see WETTING_SPEED_BLAKE) this is no longer true.

References¶

No References.

WETTING_SPEED_BLAKE¶

BC = WETTING_SPEED_BLAKE SS <bc_id> <floatlist>

Description / Usage¶

(WIC/VECTOR MOMENTUM)

This boundary condition is used to induce fluid velocity at a wetting line when using Level Set Interface Tracking. It implements a version of the Blake-DeConinck molecular-kinetic theory wetting model.

A description of the input parameters follows:

WETTING_SPEED_BLAKE	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	\(\theta_s\), the static contact angle, degrees .
<float2>	V_0 is a pre-exponential velocity factor (see functional form below).
<float3>	g is a thermally scaled surface tension, i.e. \(\sigma\)/2nkT.
<float4>	w, width of interfacial region near contact line. Defaults to level set length scale if zero or less.
<float5>	\(\beta\), slip coefficient.
<float6>	currently not used.
<float7>	currently not used.
<float8>	currently not used.

Examples¶

An example:

BC = WETTING_SPEED_BLAKE SS 10 30.0 20.1 7.0 0.   0.001 0. 0. 0.

Technical Discussion¶

The implementation for this wetting condition is identical to that of WETTING_SPEED_LINEAR, but the wetting velocity dependence is different.

Note that it is a requirement that when using this boundary condition that slip to some extent be allowed on this boundary. This is most often done by applying a VELO_SLIP_LS boundary condition in conjunction with this boundary condition. In addition, a no penetration condition on the velocity is need in either the form of a Dirichlet condition or a VELO_NORMAL condition. It is important to note that the slipping condition need not relax the no slip requirement completely. In fact, its parameters should be set so that no slip is for the most part satisfied on the boundary in regions away from the contact line. Near the contact line however the parameters in the slip condition and the WETTING_SPEED_BLAKE condition need to be fixed so that appreciable fluid velocity is induced. This is a trial and error process at the current time.

Theory¶

Derivation of this boundary condition starts with a relation propose by Blake and DeConinck for wetting line motion

This is mapped to a stress value by analogy with Navier’s slip relation,

This relation contrasts with the “linear” relation applied by the WETTING_SPEED_LINEAR relation in that the rate of change of the wetting velocity with the contact angle decreases as the wetting angle deviates more and more from its static value. This is more consisten with physical behaviors that the linear model.

In point of fact this condition is a vector condition so this scalar stress value multiplies the unit vector tangent to the surface and normal to the contact line, \(\vec{t}\) . This stress is then weighted by smooth Dirac function to restrict its location to being near the interface, weighted by a FEM shape function, integrated over the boundary sideset and added to the fluid momentum equation for the corresponding node j, vis:

References¶

No References.

WETTING_SPEED_COX¶

BC = WETTING_SPEED_COX SS <bc_id> <floatlist

Description / Usage¶

(WIC/VECTOR MOMENTUM)

This boundary condition is used to induce fluid velocity at a wetting line when using Level Set Interface Tracking. It implements a version of the Cox hydrodynamic model of wetting.

A description of the input parameters follows:

WETTING_SPEED_COX	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	\(\theta_s\), the static contact angle, degrees.
<float2>	\(\varepsilon_s\) is the dimensionless slip length, i.e. the ratio of the slip length to the characteristic length scale of the macroscopic flow.
<float3>	\(\sigma\) is the surface tension.
<float4>	w ,width of interfacial region near contact line. Defaults to level set length scale if zero or less.
<float5>	\(\beta\), slip coefficient.
<float6>	currently not used.
<float7>	currently not used.
<float8>	currently not used.

Examples¶

An example:

BC = WETTING_SPEED_COX SS 10 30.0 0.01 72.0 0.   0.001 0. 0. 0.

Technical Discussion¶

The implementation for this wetting condition is identical to that of WETTING_SPEED_LINEAR, but the wetting velocity dependence is different.

Note that it is a requirement that when using this boundary condition that slip to some extent be allowed on this boundary. This is most often done by applying a VELO_SLIP_LS boundary condition in conjunction with this boundary condition. In addition, a no penetration condition on the velocity is need in either the form of a Dirichlet condition or a VELO_NORMAL condition. It is important to note that the slipping condition need not relax the no slip requirement completely. In fact, its parameters should be set so that no slip is for the most part satisfied on the boundary in regions away from the contact line. Near the contact line however the parameters in the slip condition and the WETTING_SPEED_BLAKE condition need to be fixed so that appreciable fluid velocity is induced. This is a trial and error process at the current time.

Theory¶

Derivation of this boundary condition starts with a relation that represents the Cox hydrodynamic wetting model

See VELO_THETA_HOFFMAN for details of the Hoffman function g. Note that the convention for contact angles in this relation is that values of \(\theta\) near to zero indicate a high degree of wetting and values of \(\theta\) near 180 ° indicate the opposite. This is mapped to a stress value by analogy with Navier’s slip relation,

This relation contrasts with the “linear” relation applied by the WETTING_SPEED_LINEAR relation in that more consistent physical behavior should result.

In point of fact this condition is a vector condition so this scalar stress value multiplies the unit vector tangent to the surface and normal to the contact line, \(\vec{t}\) . This stress is then weighted by smooth Dirac function to restrict its location to being near the interface, weighted by a FEM shape function, integrated over the boundary sideset and added to the fluid momentum equation for the corresponding node j, vis:

References¶

No References.

WETTING_SPEED_HOFFMAN¶

BC = WETTING_SPEED_HOFFMAN SS <bc_id> <floatlist

Description / Usage¶

(WIC/VECTOR MOMENTUM)

This boundary condition is used to induce fluid velocity at a wetting line when using Level Set Interface Tracking. It implements a version of the Hoffman wetting correlation.

A description of the input parameters follows:

WETTING_SPEED_HOFFMAN	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	\(\theta_s\), the static contact angle, degrees .
<float2>	currently not used.
<float3>	\(\sigma\) is the surface tension.
<float4>	w, width of interfacial region near contact line. Defaults to level set length scale if zero or less.
<float5>	\(\beta\), slip coefficient.
<float6>	currently not used.
<float7>	currently not used.
<float8>	currently not used.

Examples¶

An example:

BC = WETTING_SPEED_HOFFMAN SS 10 30.0 0 72.0   0. 0.001 0. 0. 0.

Technical Discussion¶

The implementation for this wetting condition is identical to that of WETTING_SPEED_LINEAR, but the wetting velocity dependence is different.

Note that it is a requirement that when using this boundary condition that slip to some extent be allowed on this boundary. This is most often done by applying a VELO_SLIP_LS boundary condition in conjunction with this boundary condition. In addition, a no penetration condition on the velocity is need in either the form of a Dirichlet condition or a VELO_NORMAL condition. It is important to note that the slipping condition need not relax the no slip requirement completely. In fact, its parameters should be set so that no slip is for the most part satisfied on the boundary in regions away from the contact line. Near the contact line however the parameters in the slip condition and the WETTING_SPEED_BLAKE condition need to be fixed so that appreciable fluid velocity is induced. This is a trial and error process at the current time.

Theory¶

Derivation of this boundary condition starts with a relation that represents the Hoffman wetting correlation

See VELO_THETA_HOFFMAN for details of the Hoffman function g. Note that the convention for contact angles in this relation is that values of \(\theta\) near to zero indicate a high degree of wetting and values of \(\theta\) near 180 ° indicate the opposite. This is mapped to a stress value by analogy with Navier’s slip relation,

This relation contrasts with the “linear” relation applied by the WETTING_SPEED_LINEAR relation in that more consistent physical behavior should result.

In point of fact this condition is a vector condition so this scalar stress value multiplies the unit vector tangent to the surface and normal to the contact line, \(\vec{t}\) . This stress is then weighted by smooth Dirac function to restrict its location to being near the interface, weighted by a FEM shape function, integrated over the boundary sideset and added to the fluid momentum equation for the corresponding node j, vis:

References¶

Stephan F. Kistler 1993. “Hydrodynamics of Wetting” in Wettability, edited by John Berg, Surfactant Science Series, 49, Marcel Dekker, NewYork, NY, pp. 311-429.

WETTING_SPEED_LINEAR¶

BC = WETTING_SPEED_LINEAR SS <bc_id> <floatlist

Description / Usage¶

(WIC/VECTOR MOMENTUM)

This boundary condition is used to induce fluid velocity at a wetting line when using Level Set Interface Tracking.

A description of the input parameters follows:

WETTING_SPEED_LINEAR	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	\(\theta_s\), the static contact angle in degrees.
<float2>	\(c_T\), proportionality constant as defined below
<float3>	w ,width of interfacial region near contact line. Defaults to level set length scale if zero or less (L).
<float4>	\(\beta\), slip coefficient.
<float5>	currently not used.
<float6>	currently not used.
<float7>	currently not used.

Examples¶

An example:

BC = WETTING_SPEED_LINEAR SS 10 30.0 0.1 0. 0.001 0. 0. 0.

Technical Discussion¶

The prescence of wetting or contact lines in problems using level set interface tracking introduces the problem of modeling the motion of the wetting line. This boundary condition presents one potential means for doing this. It adds a wall stress value at the boundary in a region near to the wetting line (this is set with the Level Set Length Scale discussed previously). This wall stress value depends upon the deviation of the apparent contact angle determined from the level set function and a set static contact angle. The bigger the deviation in principle the bigger the induced stress. The stress is modeled by analogy with Navier’s slip relation (with slip coefficient \(\beta\)). The stress will induce a fluid velocity at the boundary which it is hoped will move the contact line at a velocity that is consistent with the rest of the flow.

An important note is that it is a requirement that when using this boundary condition that slip to some extent be allowed on this boundary. This is most often done by applying a VELO_SLIP_LS boundary condition in conjunction with this boundary condition. In addition, a no penetration condition on the velocity is need in either the form of a Dirichlet condition or a VELO_NORMAL condition. It is important to note that the slipping condition need not relax the no slip requirement completely. In fact, its parameters should be set so that no slip is for the most part satisfied on the boundary in regions away from the contact line. Near the contact line however the parameters in the slip condition and the WETTING_SPEED_LINEAR condition need to be fixed so that appreciable fluid velocity is induced. This is a trial and error process at the current time.

Theory¶

Derivation of this boundary condition starts with a simple relation for wetting line velocity

Note that the convention for contact angles in this relation is that values of \(\theta\) near to zero indicate a high degree of wetting and values of \(\theta\) near 180 ° indicate the opposite. This is mapped to a stress value by analogy with Navier’s slip relation

It should be noted that there is no distinction for this model in the function of \(\beta\) or \(c_T\). The two parameters are interchangeable. In non-linear models, (see WETTING_SPEED_BLAKE) this is no longer true.

In point of fact this condition is a vector condition so this scalar stress value multiplies the unit vector tangent to the surface and normal to the contact line, \(\vec{t}\) . This stress is then weighted by smooth Dirac function to restrict its location to being near the interface, weighted by a FEM shape function, integrated over the boundary sideset and added to the fluid momentum equation for the corresponding node j, vis:

References¶

No References.

LINEAR_WETTING_SIC¶

BC = LINEAR_WETTING_SIC SS <bc_id> <floatlist>

Description / Usage¶

(SIC/VECTOR MOMENTUM)

This boundary condition is used to induce fluid velocity at a wetting line when using Level Set Interface Tracking. It is an alternative to the WETTING_SPEED_LINEAR BC which does not require the VELO_SLIP_LS or VELO_SLIP_FILL BC’s on the wetting boundary.

A description of the input parameters follows:

LINEAR_WETTING_SIC	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	\(\theta_s\), the static contact angle in degress.
<float2>	\(c_T\), proportionality constant as defined below.
<float3>	w, width of interfacial region near contact line. Defaults to level set length scale if zero or less (L).
<float4>	\(\beta\), slip coefficient.
<float5>	\(v_{sx}\), x-component of substrate velocity.
<float6>	\(v_{sy}\), y-component of substrate velocity.
<float7>	\(v_{sz}\), z-component of substrate velocity.
<float8>	\(\tau\), stability parameter.

Examples¶

Here is an example card:

BC = LINEAR_WETTING_SIC SS 10 30.0 0.1 0. 0.001 0. 0. 0. 0.

Technical Discussion¶

This boundary condition is an additional means to impose a wetting line velocity at the contact line for level set interface tracking problems. The boundary condition uses a form of the Navier-Stokes slip condition to impose a boundary shear stress term to the momentum equation:

where \(\vec{n}\) and \(\vec{t}\) are the normal and tangent boundary vectors, respectively, \(\beta\) is the “slipping” parameter which in this context is used actually as a penalty parameter, \(\vec{v}_s\) is the substrate velocity, \(\tau\) is a stabilization parameter, \(V_{wet}\) is the wetting velocity given by the following relation

The masking function f(F) is given by the following relation as well:

where \(\alpha\) is the width of the interfacial region near the contact line itself. It has the effect of “turning off” the wetting velocity at points on the boundary away from the interface.

This constraint is then introduced into the fluid momentum equation via the weak natural boundary condition term:

When applying this boundary condition, the user should choose a value for \(\beta\) which is relatively small. Its size is dictated by the requirement that away from the interface this boundary condition should be imposing a no-slip condition on the fluid velocity. Conversely, in the vicinity of the wetting line this boundary condition will impose the wetting velocity as computed from the preceding equation.

This boundary condition probably should be used in conjunction with a no penetration boundary condition, for example, a VELO_NORMAL condition on the same sideset or potentially a Dirichlet condition on velocity if the geometry permits this. In theory, this boundary condition can be used to impose no penetration as well, but this will require a very small value for \(\beta\). The user should experiment with this.

The stability parameter, \(\tau\), as requires commentary. It is helpful to imagine that this parameter introduces a certain amount of inertia to motion of the contact line. With this term active (non-zero value for \(\tau\)), large changes of the contact line velocity with time are restricted. This can be quite helpful during startup when the intial contact angle is often very different from its equilibrium value and there can be very large velocities generated as a result. These may in turn lead to low time step size and other numerical problems.

Although every situation is different, one should choose values for \(\tau\) which are on the order of 1 to 10 times the starting time step size of the simulation. One should also recognize that this term is not consistent from a physical standpoint and therefore one should endeavor to keep \(\tau\) as small as possible if not in fact equal to zero.

References¶

No References.

BLAKE_DIRICHLET¶

BC = BLAKE_DIRICHLET SS <bc_id> <floatlist>

Description / Usage¶

(SIC/VECTOR MOMENTUM)

This boundary condition is used to induce fluid velocity at a wetting line when using Level Set Interface Tracking. It is an alternative to the WETTING_SPEED_BLAKE BC which does not require the VELO_SLIP_LS or VELO_SLIP_FILL BC’s on the wetting boundary. It uses a Blake-DeConninck relationship between apparent contact angle and wetting velocity. As the name implies, this boundary condition differs from WETTING_SPEED_BLAKE in that wetting velocity is in a strong fashion on the wetting boundary.

A description of the input parameters follows:

BLAKE_DIRICHLET	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	\(\theta_s\), the static contact angle in degrees.
<float2>	\(V_0\) is a pre-exponential velocity factor (see functional form below). (L/T)
<float3>	g is a thermally scaled surface tension, i.e. \(\sigma\)/2nkT. Note that this parameter will be multiplied by the surface tension supplied in the material file when its used in the wetting velocity relation.
<float4>	w, is the width of the interface wetting region. It defaults to the level set length scale if zero of less.
<float5>	\(\tau\), stability parameter (T).
<float6>	\(v_{sx}\), x-component of substrate velocity.
<float7>	\(v_{sy}\), y-component of substrate velocity (L/T).
<float8>	\(v_{sz}\), z-component of substrate velocity.

Examples¶

Here is an example card:

BC = BLAKE_DIRICHLET SS 10 30.0 20.1 7.0 0.0 0.001 0. 0. 0.

Technical Discussion¶

This boundary condition is an additional means to impose a wetting line velocity at the contact line for level set interface tracking problems. It is related to the WETTING_SPEED_BLAKE condition in that it uses the same Blake-DeConninck relationship between contact angle and wetting speed, but it applies this relation to the computational setting in a different way.

In this case, the following vector constraint is added to fluid momentum equation on the sideset to which this boundary condition is applied:

The factor P is a large penalty parameter which swamps any contributions from the volumetric momentum equations. Thus, the velocity, \(\sec{v}\) , on this boundary will be set solely by the preceding constraint. In this sense, it is a Dirichlet condition (strictly speaking, Dirichlet conditions involve direct substitution of nodal degrees-of-freedom with corresponding elimination of its equation from the matrix which this boundary condition does NOT do).

In the preceding, the vector \(\sec{t}\), is a tangent vector to the surface and always points in the same direction of the level set gradient on the boundary (that is, from negative to positive). In three dimensions, \(\sec{t}\) will also be normal to the contact line curve as it intersects the surface itself.

The masking function, f(\(\phi\);w) , is used to limit the application of the wetting line velocity to only that region of the boundary that is the in immediate vicinity of the contact line. We use a simple “hat” function:

Needless to say, f(\(\phi\);w) is identically zero for level set values outside the interval (-w,*w*).

The stabilization term, -\(\tau\) \(\frac{∂v}{∂t}\) , is intended to introduce something like inertia to the wetting line. That is to say, it’s primary effect is to limit the rate of change of the wetting line velocity to “reasonable” values. The \(\tau\) parameter should be chosen to be on the order of the smallest anticipated time step size in the problem. Setting it at zero, of course, will remove this term entirely.

In general, this boundary condition can be used to exclusively to set both the wetting speed velocity and the no slip requirement on the indicated sideset set. This would also include the no penetration requirement. The user may, however, find it advantageous to apply this constraint directly with the VELO_NORMAL condition on the same side set.

An additional note is that the “scaled viscosity” parameter g will be multiplied by the surface tension value supplied with Surface Tension card in the material file.

Theory¶

The wetting speed model for this boundary condition is the same used by the WETTING_SPEED_BLAKE card:

References¶

T. D. Blake and J. De Coninck 2002. “The Influence of Solid-Liquid Interactions on Dynamic Wetting”, Advances in Colloid and Interface Science, 96, 21-36.

COX_DIRICHLET¶

BC = COX_DIRICHLET SS <bc_id> <floatlist>

Description / Usage¶

(SIC/VECTOR MOMENTUM)

This boundary condition is used to induce fluid velocity at a wetting line when using Level Set Interface Tracking. It is an alternative to the WETTING_SPEED_COX which does not require the VELO_SLIP_LS or VELO_SLIP_FILL BC’s on the wetting boundary. It implements a version of the Cox hydrodynamic model of wetting (see below). As the name implies, this boundary condition differs from WETTING_SPEED_COX in that wetting velocity is applied in a strong fashion on the wetting boundary.

A description of the input parameters follows:

COX_DIRICHLET	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	\(\theta_s\), the static contact angle in degress.
<float2>	\(\varepsilon_s\) is the dimensionless slip length, i.e. the ratio of the slip length to the characteristic length scale of the macroscopic flow. (L)
<float3>	\(\sigma\) is the surface tension. Note this value will be scaled by the surface tension value supplied in the material file.(F/L)
<float4>	w, is the width of the interface wetting region. It defaults to the level set length scale if zero of less (L).
<float5>	\(\tau\), stability parameter (T).
<float6>	\(v_{sx}\), x-component of substrate velocity.
<float7>	\(v_{sy}\), y-component of substrate velocity (L/T).
<float8>	\(v_{sz}\), z-component of substrate velocity.

Examples¶

Here is an example card:

BC = COX_DIRICHLET SS 10 30.0 0.01 72.0   0. 0.001 0. 0. 0.

Technical Discussion¶

This boundary condition is applied in exactly the same manner as the BLAKE_DIRICHLET boundary condition. The only substantial difference is the model used to derive the wetting speeds relation to the local apparent contact angle. The reader is referred to the BLAKE_DIRICHLET section of the manual for further reference.

Theory¶

This boundary condition uses this relation that represents the Cox hydrodynamic wetting model

See VELO_THETA_COX for details of the Cox functions f and g. Note that the parameters \(\lambda\), \(q_{inner}\), and \(q_{outer}\) are currently not accessible from the input card and are hard-set to zero. \(\lambda\) is the ratio of gas viscosity to liquid viscosity whereas \(q_{inner}\) and \(q_{outer}\) represent influences from the inner and outer flow regions.

References¶

Stephan F. Kistler 1993. “Hydrodynamics of Wetting” in Wettability, edited by John Berg, Surfactant Science Series, 49, Marcel Dekker, NewYork, NY, pp. 311-429.

HOFFMAN_DIRICHLET¶

BC = HOFFMAN_DIRICHLET SS <bc_id> <floatlist>

Description / Usage¶

(SIC/VECTOR MOMENTUM)

This boundary condition is used to induce fluid velocity at a wetting line when using Level Set Interface Tracking. It is an alternative to the WETTING_SPEED_HOFFMAN boundary condition which does not require the VELO_SLIP_LS or VELO_SLIP_FILL BC’s on the wetting boundary. As the name implies, this boundary condition differs from WETTING_SPEED_HOFFMAN in that wetting velocity is in a strong fashion on the wetting boundary.

A description of the input parameters follows:

HOFFMAN_DIRICHLET	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	\(\theta_s\), the static contact angle in degress.
<float2>	not used.
<float3>	\(\sigma\), the surface tension. Note that this parameter will be scaled by the surface tension value supplied in the material file. (F/L)
<float4>	w, is the width of the interface wetting region. It defaults to the level set length scale if zero of less.
<float5>	\(\tau\), stability parameter (T).
<float6>	\(v_{sx}\), x-component of substrate velocity.
<float7>	\(v_{sy}\), y-component of substrate velocity (L/T).
<float8>	\(v_{sz}\), z-component of substrate velocity.

Examples¶

Here is an example card:

BC = HOFFMAN_DIRICHLET SS 10 30.0 0 72.0 0.0 0.001 0. 0. 0.

Technical Discussion¶

The technical details of the application of this boundary differ not at all from those described for the BLAKE_DIRICHLET boundary condition. The user is referred to that section for further details. This boundary condition differs only in the model used to determine the wetting velocity. This is described below and in the VELO_THETA_HOFFMAN card.

Theory¶

Derivation of this boundary condition starts with a relation that represents the Hoffman wetting correlation

See VELO_THETA_HOFFMAN for details of the Hoffman function g. Note that the convention for contact angles in this relation is that values of \(\theta\) near to zero indicate a high degree of wetting and values of \(\theta\) near 180 ° indicate the opposite. This is mapped to a stress value by analogy with Navier’s slip relation,

References¶

Stephan F. Kistler 1993. “Hydrodynamics of Wetting” in Wettability, edited by John Berg, Surfactant Science Series, 49, Marcel Dekker, NewYork, NY, pp. 311-429.

VELO_SLIP_LS¶

BC = VELO_SLIP_LS SS <bc_id> <float_list>

Description / Usage¶

(WIC/VECTOR MOMENTUM)

This boundary condition is applied only in problems involving embedded interface tracking, that is, level set or volume of fluid. The boundary condition serves two major purposes: first to allow for slip in the vicinity of a moving contact line and second to facilitate impact of a dense fluid on a substrate, displacing a less dense fluid (e.g. water drop and air displacement). . Elsewhere, this boundary condition enforces a no-slip condition between fluid and substrate. A more detailed description is given below.

This boundary condition is most often used in conjunction with the FILL_CA, WETTING_SPEED_LINEAR, or WETTING_SPEED_BLAKE boundary conditions. These apply forces to contact lines in order to simulate wetting line motion. These forces are applied in a weak sense to the same regions near the interface so it is necessary to use VELO_SLIP_LS with a large slipping coefficient so that effectively no-slip is relaxed completely near the interface.

Definitions of the input parameters are as follows:

VELO_SLIP_LS	Name of the boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>	alpha, or slip_width, a characteristic length scale around the contact line that will be used to apply Navier Slip Condition with \(\beta\) 0 coefficient. This length scale is also used to detect the thickness of light-phase (gas) between the substrate denoted by the sideset, and the zero-level-set contour (or the boundary between liquid and gas). If this distance is less than 8*slip_width, then perfect slip in the gas phase is allowed to help facilitate contact. See discussion below.
<float2>	\(\beta\) 0, the slip coefficient near the contact line. The inverse of \(\beta\) 0 defines the scaling between stress and slip. The parameter supplied on the input deck is used only within a lengthscale slip_width setting around the contact line.. Elsewhere, the slip coefficient is uniformly set to \(\beta\) 1. Hence, this parameter is usually set to a large value to allow for perfect slip.
<float3>	\(v_{s,x}\), the x-component of surface velocity vector. This would be the x-component of the fluid velocity if a noslip condition were applied.
<float4>	\(v{s,y}\), the y-component of surface velocity vector. This would be the y-component of the fluid velocity if a noslip condition were applied.
<float5>	\(v_{s,z}\), the z-component of surface velocity vector. This would be the z-component of the fluid velocity if a noslip condition were applied.
<float6>	\(\beta\) 1, the slip coefficient away from the contact line. The inverse of \(\beta\) 1 defines the scaling between stress and slip. Hence, this parameter is usually set to a small value (like 1e-6) to allow for no-slip.

Examples¶

Following is a sample card without the optional parameters:

BC = VELO_SLIP_LS SS 10 0.05 100000.0 0.0 0.0 1.e-6

The large value of slip coefficient ensures nearly perfect slip in the region around the interface, a region that has a half-width of 0.05 centered about the contact line. Away from the contact line (outside the hat function of width 0.05), the slip coefficient is 1.e-6, which corresponds to significantly less slip. Note also that if the substrate defined by SS 10 is in contact with gas (light phase), and a liquid front (zero-level set) is nearby, or within a distance 8 times 0.05, then the light phase is allowed to slip along the wall with a coefficient of 100000.0. This is to help facilitate contact.

Technical Discussion¶

This boundary condition was originally developed to allow for fluid slip near a dynamic contact line, a necessary condition for dynamic wetting line motion when the contact angle is not 180 degrees (viz. rolling motion condition). The slippage mechanism was deployed through the use of Navier’s slip condition, which basically goes as

Here \(\beta\) is the slip coefficient, which is taken to be variable depending on its proximity to the contact line (through the “slip_width” parameter). Note that the smaller the \(\beta\), the more no-slip is enforced. The left hand side of this condition is the fluid traction on the substrate. \(\underline{v}_s\) is the velocity of the substrate, specified component-wise with {vx} {vy} {vz}. This base functionality of applying the Navier slip condition still exists in this condition, but in addition it was furbished to allow for complete slip on the boundary if a gas film is being displaced by liquid. In this latter case, complete slip is a mechanism (subgrid event) that allows for the otherwise infinite stress to be relieved so that the liquid can make contact with the solid. The perfect slip condition at the substrate/gas surface is activated by just setting the slip coefficient to the large value, as this condition does anyway in the vicinity of a contact line. The “gas phase” is determined by determining which phase is the lighter one based on the density specification. The figure below details more on how this condition works for wetting/dewetting and for incipient liquid/solid impact.

Some more usage notes as follows:

The slip coefficient function is computed as \(\beta\) = \(\beta\) 0 \(\delta\) ( \(\phi\) ) + \(\beta_\infty\), where the delta function is a level-set hat function centered around the zero level set contour where it intersects the boundary. It has a length sacale associated with it which is called “alpha”, and that basically sets the length over which the \(\beta\) 0 is applied as the slip parameter and it is large, leading to a shear-stress-free or slippery region in both the gas and liquid phases. \(\beta_{INF}\) is taken as real small (typically 1.e-6 or less) and is applied away from the contact line, and hence forces a true “no-slip” condition.
The most recent addition to this condition is the functionality that adds perfect slip to a wall in the gas phase as it is displaced during near contact state by a liquid phase. This capability is of course applicable only to level-set capillary hydrodynamics problems. Level-set methods have been plagued by the fact that it is hard to break down the displaced phase (e.g. gas phase) as a liquid phase surface flows towards a solid boundary. Theoretically this event requires an infinite stress, in the continuum. To relieve this stress and promote a collapse and wetting, we add perfect slip in the gas phase at near contact conditions, which reduces the lubrication pressure in the gas film and promotes breakdown. This of course introduces more length scales. First, the length scale over which slip is applied (this is the alpha parameter described above) and seond is the length scale over which “nearness” of the liquid phase to the substrate is considered to be “close enough” to allow for perfect slip. Right now this “nearness” length scale is arbitrarily set to 8*alpha. A third length scale is that which we use to declare contact. We currently have that set to 1.e-6*alpha. After contact is declared, VELO_SLIP_LS reverts to the form under the first bullet. The figure below hopefully clarifies the condition a little better.

Category 16: Shell Equations¶

These boundary conditions are applied to shell equations, a special category of equations applied on 1D boundaries of 2D surfaces in Goma.

SHELL_SURFACE_CHARGE¶

BC = SHELL_SURFACE_CHARGE SS <bc_id> <integer>

Description / Usage¶

(WIC/POTENTIAL)

This boundary condition card is used to add to the potential equation the surface charge term at a shell surface. Definitions of the input parameters are as follows:

SHELL_SURFACE_CHARGE	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain. This boundary must coincide with the shell element block on which the surface charge equation is applied.
<integer>	Integer value indicating the bulk element block ID from which to apply the boundary condition (not currently implemented).

This boundary condition is currently inoperative.

Examples¶

For a system consisting of a solid material (element block ID 1) with a conducting shell surface (element block ID 2) whose location coincides with side set 20, the following is a sample usage:

BC = SHELL_SURFACE_CHARGE SS 20 1

Technical Discussion¶

This boundary condition was originally developed to allow for fluid slip near a dynamic contact line, a necessary condition for dynamic wetting line motion when the contact angle is not 180 degrees (viz. rolling motion condition). The slippage mechanism was deployed through the use of Navier’s slip condition, which basically goes as

where E is the electric field vector, the superscripts (o) and (i) denote the outer and inner phases, n is a unit normal pointing into the outer phase, \(\varepsilon\) is the electrical permittivity, E = –\(\Delta\) V is the electric field and V is the voltage or electric potential.

SHELL_SURFACE_CHARGE_SIC¶

BC = SHELL_SURFACE_CHARGE_SIC SS <bc_id> <integer>

Description / Usage¶

(WIC/POTENTIAL)

This boundary condition card is used to add to the potential equation the surface charge term at a shell surface. Physically it is the same as the SHELL_SURFACE_CHARGE boundary condition, but is applied as a strongly-integrated condition. Definitions of the input parameters are as follows:

SHELL_SURFACE_CHARGE_SIC	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain. This boundary must coincide with the shell element block on which the surface charge equation is applied.
<integer>	Integer value indicating the bulk element block ID from which to apply the boundary condition (not currently implemented).

This boundary condition is currently inoperative…

Examples¶

For a system consisting of a solid material (element block ID 1) with a conducting shell surface (element block ID 2) whose location coincides with side set 20, the following is a sample usage:

BC = SHELL_SURFACE_CHARGE_SIC SS 20 1

Technical Discussion¶

This boundary condition applies a surface charge balance along the shell: surface.. In its most general form, this balance is written

where E is the electric field vector, the superscripts (o) and (i) denote the outer and inner phases, n is a unit normal pointing into the outer phase, \(\varepsilon\) is the electrical permittivity, \(\underline{E}\) = –\(\Delta\) V is the electric field and V is the voltage or electric potential.

SURFACE_ELECTRIC_FIELD¶

BC = SURFACE_ELECTRIC_FIELD SS <bc_id> <integer> <integer> <integer>

Description / Usage¶

(WSG/SURFACE CHARGE)

This boundary condition card is used to apply a part of the shell surface charge equation which includes the electric field, the negative gradient of the potential variable which is applied on a neighboring bulk block. It is actually an integral part of the surface charge equation. Definitions of the input parameters are as follows:

SURFACE_ELECTRIC_FIELD	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain. This boundary must coincide with the shell element block on which the surface charge equation is applied.
<integer>	Bulk element block ID (from ExodusII database) for neighboring bulk element block on which the potential equation is applied.
<integer>	Shell element block ID (from ExodusII database) for shell block on which the surface charge equation is applied.

This boundary condition is currently inoperative…

Examples¶

For a system consisting of a solid material (element block ID 1) with a conducting shell surface (element block ID 2) whose location coincides with side set 20, the following is a sample usage:

BC = SURFACE_ELECTRIC_FIELD SS 20 1 2

Technical Discussion¶

This is a special type of boundary condition, WEAK_SHELL_GRAD, which is a portion of a shell equation which involves spatial gradients of bulk variables. Since the values of bulk variable gradients depend on all of the degrees of freedom of that variable in the bulk element, and sensitivities to the off-shell degrees of freedom must be applied, a portion of the equation must be evaluated from the bulk side. This is done in Goma by means of a WEAK_SHELL_GRAD boundary condition which evaluates these terms and all bulk sensitivities from the bulk side, the saves these values for later recall when the rest of the surface charge equation is assembled.

In this case, the term n • \(\Delta\) V and its potential sensitivities are evaluated within the bulk element for inclusion in the surface charge balance along the shell surface.. I

References¶

No References.

SH_TENS¶

BC = SH_TENS NS <bc_id> <float1> [float2]

Description / Usage¶

(DC/shell_tension)

This Dirichlet boundary condition specification is used to set a tension (in stress per unit length) to the inextensible shell equations (see EQ = shell_tension and EQ = shell_curvature) at an endpoint. This boundary condition can be applied in two dimensions only, and only to the endpoint of a bar-type element. In put is as follows :

SH_TENS	Boundary condition name (<bc_name>) that defines the shell tension (compressive or expansion depending on the sign).
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database. Note that this must be a single-node node set representing and endpoint to a bar element type.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	Value of tension.
[float2]	An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

The following is a sample card for applying a Dirichlet condition on the tension for a shell equation:

BC = SH_TENS NS 100 10.

This condition sets a tension of 10.0 at Nodeset 100.

Technical Discussion¶

No Discussion.

References¶

GT-027.1: GOMA’s Shell Structure Capability: User Tutorial (GT-027.1)

SH_K¶

BC = SH_K NS <bc_id> <float1> [float2]

Description / Usage¶

(DC/shell_curvature)

This Dirichlet boundary condition specification is used to set a curvature to the inextensible shell equations (see EQ = shell_tension and EQ = shell_curvature) at an endpoint. This boundary condition can be applied in two dimensions only, and only to the endpoint of a bar-type element:

SH_K	Boundary condition name (<bc_name>) that defines the shell curvature.
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database. Note that this must be a single-node node set representing and endpoint to a bar element type.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	Value of curvature.
[float2]	An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

The following is a sample card for applying a Dirichlet condition on the curvature for a shell equation:

BC = SH_K NS 100 0.

This condition sets a curvature of zero at Nodeset 100.

Technical Discussion¶

No Discussion.

References¶

GT-027.1: GOMA’s Shell Structure Capability: User Tutorial (GT-027.1)

SH_FLUID_STRESS¶

BC = SH_FLUID_STRESS SS <bc_id> <float>

Description / Usage¶

(PCC/VECTOR MOMENTUM)

Used for fluid-structure interaction problems with structural shell elements, the SH_FLUID_STRESS condition equates the normal traction (the tangential and normal force components, per unit area) between adjacent fluid and solid structure. This condition is only to be used on boundaries between regions of ARBITRARY mesh motion with fluid momentum equations: see Mesh Motion and EQ cards. With this boundary condition, the local residual and Jacobian contributions from the fluid mechanics momentum equations (on the ARBITRARY side of the boundary) are added into weak form of the residual and Jacobian entries for the solid structural equations (see EQ = shell_curvature and EQ = shell_tension). All elements on both sides of the interface must have the same element type, i.e., the same order of interpolation and basis functions, e.g., Q1 fluid and Q1 (bar element) for shell. Q2 fluid momentum and Q2 (bar element) for the shell equations. Also, such interfaces must be defined as a mesh side set attached to the bulk fluid elements (most mesh generators will not allow for side sets in bar or sheet elements).

Definitions of the input parameters are as follows:

SH_FLUID_STRESS	Name of the boundary condition (<bc_name>).
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float>	Scale factor for stress balance for non-dimensionalization. This parameter, which multiplies the liquid phase contribution and should be set to 1.0 if there is no nondimensional treatment.

Examples¶

The following is a sample input card:

BC = SH_FLUID_STRESS SS 5 1.0

In this example, side set 5 is a boundary between a solid blade and a liquid; material 2 is the rubber blade, and material 1 is the fluid. Along that blade, a companion boundary condition of the form

BC = NO_SLIP SS 5 2 1

should also be applied.

Technical Discussion¶

The functional form of the boundary condition is:

where \(\underline{T}\) is the fluid phase stress tensor given by any one of the specified fluid-phase constitutive equations, and \(\underline\sigma\) is the solid-phase stress tensor, also given by any one of the solid-phase constitutive equation (see material file specifications). \(\lambda\) is a scaling factor that defaults to unity (and is usually best taken as such unless some scaling is invoked).

This balance is applied to the weak form of the solid-phase momentum residuals, from the fluid phase, viz. in the fluid-phase, the fluid-stress at the interface is added to the solid-phase momentum residuals. As mentioned above, this condition usually needs to be supplemented by a statement of mass conservation across the interface, which will depend on whether the solid phase is of CONTINUOUS or POROUS media (see Media Type card).

FAQs¶

Troubleshooting 1: This boundary condition requires that the side set contain elements from both the fluid and the solid side of the interface. For the FASTQ tool, this is the default case; for CUBIT and possibly other related tools, this can be forced on the side set definition options. Interestingly, the boundary condition does work if the side set is attached to the fluid phase only, but just due to the way in which it is applied.
Troubleshooting 2: This boundary condition does not enforce mass conservation. A combination of NO_SLIP or VELO_NORMAL/VELO_TANGENT must be invoked to achieve a material surface. For the latter, care must be taken to maintain the application of the VELO_NORMAL condition after a remesh. This condition is applied only to one side of the interface and depends on the ss_to_blks connectivity structure; it may be necessary to force its application, especially after remeshes. To be sure that the proper set of conditions is being applied, look at the BC_dup.txt file for nodes along the interface.

References¶

GT-003.1: Roll coating templates and tutorial for GOMA and SEAMS, February 29, 2000, P. R. Schunk and Matt Stay

GT-006.3: Slot and Roll coating with remeshing templates and tutorial for GOMA and CUBIT/MAPVAR, August 3, 1999, R. R. Lober and P. R. Schunk

LUB_PRESS¶

BC = LUB_PRESS NS <bc_id> <float_list>

Description / Usage¶

This boundary condition card applies a lubrication pressure to the boundary of a shellelement sheet. The corresponding equation is EQ=lubp. The boundary condition is applied to a node set.

LUB_PRESS	Name of boundary condition.
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	lub_p, the value of lubrication pressure at the boundary.
[float2]	Optional floating point number set between 0.0 and 1.0 which serves as a flag to the code for a Dirichlet boundary condition. If this value is present, and is not 1.0, the condition is applied as a residual equation. Otherwise, it is “hard-set” condition and is eliminate from the matrix. The residual method must beused when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

Following is a sample card:

BC = LUB_PRESS NS   100 100.

This condition applies a lubrication pressure of 100.0 at nodeset 100.

Technical Discussion¶

The equation applied at the specified nodeset in place of Reynold’s lubrication equation for confined flow. Note that it is not to be used for the film-flow lubrication equations.

GRAD_LUB_PRESS¶

BC = GRAD_LUB_PRESS SS <bc_id> <float1>

Description / Usage¶

(WIC/R_LUBP)

This boundary condition card applies free boundary condition, akin to Papanastasiou et al. (1992) for the fluid momentum, at the boundary of a shell-element sheet. The boundary condition is applied to a sideset.

GRAD_LUB_PRESS	Name of boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	Flowrate in L^2/t. Usually set for NOBC effect.

Examples¶

Following is a sample card:

BC = GRAD_LUB_PRESS SS   100 0.

This condition applied at sideset 100.

Technical Discussion¶

No Discussion.

SHELL_FILMP¶

BC = SHELL_FILMP NS <bc_id> <float_list>

Description / Usage¶

This boundary condition card applies a film pressure to the boundary of a shell-element sheet. The corresponding equation is EQ=shell_filmp. The boundary condition is applied to a node set.

SHELL_FILMP	Name of boundary condition.
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	shell_filmp, the value of lubrication pressure at the boundary.
[float2]	Optional floating point number set between 0.0 and 1.0 which serves as a flag to the code for a Dirichlet boundary condition. If this value is present, and is not 1.0, the condition is applied as a residual equation. Otherwise, it is “hard-set” condition and is eliminate from the matrix. The residual method must beused when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

Following is a sample card:

BC = SHELL_FILMP NS   100 100.

This condition applies a film pressure of 100.0 at nodeset 100.

Technical Discussion¶

The equation applied at the specified nodeset in place of the film-flow lubrication equation.

SHELL_FILMH¶

BC = SHELL_FILMH NS <bc_id> <float_list>

Description / Usage¶

(DC/R_SHELL_FILMH)

This boundary condition card applies a film height to the boundary of a shell-element sheet. The corresponding equation is EQ=shell_filmh. The boundary condition is applied to a node set.

SHELL_FILMH	Name of boundary condition.
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	shell_filmh, the value of film thickness at the boundary.
[float2]	Optional floating point number set between 0.0 and 1.0 which serves as a flag to the code for a Dirichlet boundary condition. If this value is present, and is not 1.0, the condition is applied as a residual equation. Otherwise, it is “hard-set” condition and is eliminate from the matrix. The residual method must beused when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

Following is a sample card:

BC = SHELL_FILMH NS   100 1.

This condition applies a film height of 1.0 at nodeset 100.

Technical Discussion¶

The equation applied at the specified nodeset in place of the film-flow height equation.

SHELL_PARTC¶

BC = SHELL_PARTC NS <bc_id> <float_list>

Description / Usage¶

(DC/R_SHELL_PARTC)

This boundary condition card applies a particle volume fraction to the boundary of a shell-element sheet. The corresponding equation is EQ=shell_filmh. The boundary condition is applied to a node set.

SHELL_PARTC	Name of boundary condition.
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	shell_partc, the value of film thickness at the boundary.
[float2]	Optional floating point number set between 0.0 and 1.0 which serves as a flag to the code for a Dirichlet boundary condition. If this value is present, and is not 1.0, the condition is applied as a residual equation. Otherwise, it is “hard-set” condition and is eliminate from the matrix. The residual method must beused when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

Following is a sample card:

BC = SHELL_PARTC NS   100 0.

This condition applies a particles volume fractioin of 0.0 at nodeset 100.

Technical Discussion¶

The equation applied at the specified nodeset in place of the particles conservation equation.

References¶

No References.

SHELL_GRAD_FP¶

BC = BC = SHELL_GRAD_FP SS <bc_id> <float_list>

Description / Usage¶

(SIC/R_SHELL_GRAD_FP)

This boundary condition card applies a volumetric flux of liquid film to the boundary of a shell-element sheet. The corresponding equation is EQ=shell_filmp. The boundary condition is applied to a node set.

SHELL_GRAD_FP	Name of boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	volumetric flux

Examples¶

Following is a sample card:

BC = SSHELL_GRAD_FP SS   100 0.0

This condition applies a particles volume flux of 0.0 at nodeset 100.

Technical Discussion¶

The actual weighted residual equation that is applied to node on the surface is

where \(\phi_i\) is the finite element trial function, n is the outward-pointing normal to the surface, and q is the volumetric flux specified in the <float1>. Careful attention should be given for the sign of q. The sign convention is that q is positive when the flow is exiting the boundary and negative when entering the boundary.

The condition replaces the residual equation shell_filmp at the boundary.

SHELL_GRAD_FP_NOBC¶

BC = BC = SHELL_GRAD_FP_NOBC SS <bc_id>

Description / Usage¶

(WIC/R_SHELL_GRAD_FP_NOBC)

This boundary condition card applies free boundary condition, akin to Papanastasiou et al. (1992) for the fluid momentum, at the boundary of a shell-element sheet. The boundary condition is applied to a sideset.

SHELL_GRAD_FP_NOBC	Name of boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.

Examples¶

Following is a sample card:

BC = SSHELL_GRAD_FP_NOBC SS   100

This condition applied at sideset 100.

Technical Discussion¶

The finite element formulation of the first equation of the film profile equation boundary integral in the form of

This condition is similar to the SHELL_GRAD_FP boundary condition, except that the condition is now a weak integrated condition that is added to the residual equations, instead of replacing them and the flux is no longer specified.

SHELL_GRAD_FH¶

BC = BC = SHELL_GRAD_FH SS <bc_id> <float_list>

Description / Usage¶

(SIC/R_SHELL_GRAD_FH)

This boundary condition card sets a slope to the liquid film at the boundary of a shellelement sheet. The corresponding equation is EQ=shell_filmh. The boundary condition is applied to a node set.

SHELL_GRAD_FH	Name of boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	slope

Examples¶

Following is a sample card:

BC = SSHELL_GRAD_FH SS   100 0.0

This condition applies a film slope of 0.0 at nodeset 100.

Technical Discussion¶

he actual weighted residual equation that is applied to node on the surface is

where \(\phi_i\) is the finite element trial function, n is the outward-pointing normal to the surface, \(\Sigma\) and is the slope specified in the <float1>.

The condition replaces the residual equation shell_filmh at the boundary.

SHELL_GRAD_FH_NOBC¶

BC = BC = SHELL_GRAD_FH_NOBC SS <bc_id>

Description / Usage¶

(WIC/R_SHELL_GRAD_FH_NOBC)

This boundary condition card applies free boundary condition, akin to Papanastasiou et al. (1992) for the fluid momentum, at the boundary of a shell-element sheet, in terms of the slope of a thin Reynolds film. The boundary condition is applied to a sideset.

SHELL_GRAD_FH_NOBC	Name of boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.

Examples¶

Following is a sample card:

BC = SSHELL_GRAD_FH_NOBC SS   100

This condition applied at sideset 100.

Technical Discussion¶

The finite element formulation of the second equation of film profile equation generates boundary integral in the form of

This condition is similar to the SHELL_GRAD_FH boundary condition, except that the condition is now a weak integrated condition that is added to the residual equations, instead of replacing them and the flux is no longer specified.

SHELL_GRAD_PC¶

BC = BC = SHELL_GRAD_PC SS <bc_id> <float_list>

Description / Usage¶

(WIC/R_SHELL_GRAD_PC)

This boundary condition card allows the user to set volumetric flux of particles inside liquid film at the boundary of a shell-element sheet. The corresponding equation is EQ=shell_partc. The boundary condition is applied to a side set.

SHELL_GRAD_PC	Name of boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	particle flux

Examples¶

Following is a sample card:

BC = SHELL_GRAD_PC SS   100 1.

This condition applied at sideset 100. and sets a particle flux to 1.0

Technical Discussion¶

The actual weighted residual equation that is applied to node on the surface is

where \(\phi_i\) is the finite element trial function, n is the outward-pointing normal to the surface, \(J_p\) and is the particles flux specified in the <float1>.

The condition replaces the residual equation shell_partc at the boundary.

SHELL_LUBP_SOLID¶

BC = SH_LUBP_SOLID SS <bc_id> <float1>

Description / Usage¶

(WIC/R_MESH1/R_MESH2/RMESH3)

This vector boundary condition card balances the stress in an abutting continuum elastic solid with the lubrication forces (pressure and shear) in a surface shell. The boundary condition is applied to a sideset. Please see notes below on the sideset features which must be specified.

SH_LUBP_SOLID	Name of boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes sideset in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (nodeset in EXODUS II) in the problem domain.
<float1>	Scaling factor. Normally set this to 1.0, unless a stressbalance scale is required due to nondimensionalization.

Examples¶

Following is a sample card:

BC = SH_LUBP_SOLID SS   100 1.0

This boundary condition is applied at sideset 100.

Technical Discussion¶

The mathematical form of the boundary condition is

This condition is similar to FLUID_SOLID and SOLID_FLUID boundary conditions for the case of fluid-structure interaction between two continuum regions, one fluid and one solid.
Note that the sideset as generated in CUBIT or related software is actually attached to the continuum domain and not the shell face, as those faces (top and bottom of sheet and not the edges) are not true finite element sides. Most mesh generators will not allow sidesets to be include shell element faces. GOMA figures out the right thing to do.

SHELL_TEMP¶

BC = SHELL_TEMP NS <bc_id> <float_list>

Description / Usage¶

(DC/R_SHELL_ENERGY)

This boundary condition card applies a shell temperature to the boundary of a shellelement sheet. The corresponding equation is EQ=shell_energy. The boundary condition is applied to a node set.

SHELL_TEMP	Name of boundary condition.
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	SHELL_TEMP, the value of temperature at the boundary.
[float2]	Optional floating point number set between 0.0 and 1.0 which serves as a flag to the code for a Dirichlet boundary condition. If this value is present, and is not 1.0, the condition is applied as a residual equation. Otherwise, it is “hard-set” condition and is eliminated from the matrix. The residual method must beused when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

Following is a sample card:

BC = SHELL_TEMP 100 1.0

This boundary condition is applied at nodeset 100.

Technical Discussion¶

The equation applied at the specified nodeset in place of the shell-temperature equation.

References¶

No References.

SHELL_OPEN_PRESS, SHELL_OPEN_PRESS_2¶

BC = SHELL_OPEN_PRESS NS <bc_id> <float_list>

BC = SHELL_OPEN_PRESS_2 NS <bc_id> <float_list>

Description / Usage¶

(DC/R_SHELL_SAT_OPEN or SHELL_SAT_OPEN_2)

This Dirichlet boundary condition card applies a shell liquid phase pressure to the boundary of a shell-element sheet. The corresponding equation is EQ=shell_sat_open or correspondingly shell_sat_open_2, depending on which layer. The boundary condition is applied to a node set.

SHELL_OPEN_PRESS	Name of boundary condition.
NS	Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>	SHELL_OPEN_PRESSURE, the value of the liquid phase pressure at the boundary.
[float2]	Optional floating point number set between 0.0 and 1.0 which serves as a flag to the code for a Dirichlet boundary condition. If this value is present, and is not 1.0, the condition is applied as a residual equation. Otherwise, it is “hard-set” condition and is eliminated from the matrix. The residual method must beused when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

Following is a sample card:

BC = SHELL_OPEN_PRESS 100 1.0

This boundary condition is applied at nodeset 100.

Technical Discussion¶

The equation applied at the specified nodeset in place of the shell-sat-open equation.

References¶

No References.

LUBP_SH_FP_FLUX¶

C = LUBP_SH_FP_FLUX SS <bc_id> <int1> <int2>

Description / Usage¶

(COLLOC/R_SHELL_FILMP)

This boundary condition card matches the mass flux in one region of confined flow (lubp) to the mass flux from a second region of film flow (shell_filmp). The flux matching is handled as a sideset between two shell regions. In this way both equations can be coupled for exit or entrance flows. The boundary condition is applied in collocated form, and replaces the R_SHELL_FILMP equation.

LUBP_SH_FP_FLUX	Name of boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<int1>	Block id of mesh material which invokes the lubp equation.
<int2>	Block id of mesh material which invokes the shell_filmp equation.

Examples¶

Following is a sample card:

BC = LUBP_SH_FP_FLUX SS   100 2 1

This condition applies the matching tie condition at a side set boundary between block 2 (which invokes the EQ = lubp equation) and block 1 (which invokes the EQ=shell_filmp equation).

Technical Discussion¶

The best example of the use of this equation is the exit of a metered coating flow. It must be used together with a pressure-matching condition LUBP_SH_FP_MATCH.

LUBP_SH_FP_MATCH¶

C = LUBP_SH_FP_MATCH SS <bc_id> <int1> <int2>

Description / Usage¶

(STRONG_INT_SURF/R_LUBP)

This boundary condition card matches the pressure in one region of confined flow (lubp) to the pressure from a second region of film flow (shell_filmp). The pressure matching is handled as a sideset between two shell regions. In this way both equations can be coupled for exit or entrance flows. The boundary condition is applied in collocated form, and replaces the R_LUBP equation.

LUBP_SH_FP_FLUX	Name of boundary condition.
SS	Type of boundary condition (<bc_type>), where SS denotes node set in the EXODUS II database.
<bc_id>	The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<int1>	Block id of mesh material which invokes the lubp equation.
<int2>	Block id of mesh material which invokes the shell_filmp equation.

Examples¶

Following is a sample card:

BC = LUBP_SH_FP_MATCH SS   100 2 1

This condition applies the matching tie condition at a side set boundary between block 2 (which invokes the EQ = lubp equation) and block 1 (which invokes the EQ=lubp equation).

Technical Discussion¶

The best example of the use of this equation is the exit of a metered coating flow. It must be used together with a flux-matching condition LUBP_SH_FP_FLUX.

Category 17: Acoustic Equations¶

These boundary conditions are applied to acoustic equations (Preal, Pimag, Reyn_stress).

APR¶

BC = APR NS <bc_id> <float1> [float2]

Description / Usage¶

(DC/ACOUS_PREAL)

This Dirichlet boundary condition card is used to set constant amplitude of the real part of the acoustic pressure. Definitions of the input parameters are as follows:

APR: Name of the boundary condition (<bc_name>).
NS: Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>: The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>: Value of the real part of the acoustic pressure amplitude.
[float2]: An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

The following is a sample input card:

BC = APR NS 100 1000.0

APR_PLANE_TRAN¶

BC = APR_PLANE_TRAN SS <bc_id> <float1>

Description / Usage¶

(WIC/SCALAR ACOUS_PREAL)

This boundary condition card applies the plane wave transmission conditions to the acoustic wave equations. This card concerns the real part while API_PLANE_TRAN concerns the imaginary component. This condition is used to set reflection/ transmission conditions for a surrounded material that is not being meshed. Definitions of the input parameters are as follows:

APR_PLANE_TRAN: Name of the boundary condition (<bc_name>).
SS: Type of boundary condition (<bc_type>), where SS denotes side set.
<bc_id>: The boundary flag identifier, or a side set number which is an integer that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>: \(R_2\), the acoustic impedance (i.e. product of density and wave speed) in the surrounded material.

Examples¶

The following is a sample input card:

BC = APR_PLANE_TRAN SS 10 0.1

Technical Discussion¶

This condition should be used to account for transmission/reflection conditions for the external boundaries when the acoustic wave equation is used. It reflects characteristics for an acoustic wave encountering a planar interface between two materials;

where k is the acoustic wavenumber and R is the acoustic impedance. The subscript 1 refers to the material inside the external boundary and is the material which is meshed. Subscript 2 refers to the material outside of the external boundary. If \(R_2\) is set equal to \(R_1\), then this condition mimics an infinite boundary condition, i.e. no reflection at the external boundary.

API¶

BC = API NS <bc_id> <float1> [float2]

Description / Usage¶

(DC/ACOUS_PIMAG)

This Dirichlet boundary condition card is used to set constant amplitude of the imaginary part of the acoustic pressure. Definitions of the input parameters are as follows:

API: Name of the boundary condition (<bc_name>).
NS: Type of boundary condition (<bc_type>), where NS denotes node set in the EXODUS II database.
<bc_id>: The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (node set in EXODUS II) in the problem domain.
<float1>: Value of the imaginary part of the acoustic pressure amplitude.
[float2]: An optional parameter (that serves as a flag to the code for a Dirichlet boundary condition). If a value is present, and is not -1.0, the condition is applied as a residual equation. Otherwise, it is a “hard set” condition and is eliminated from the matrix. The residual method must be used when this Dirichlet boundary condition is used as a parameter in automatic continuation sequences.

Examples¶

The following is a sample input card:

BC = API NS 100 1000.0

API_PLANE_TRAN¶

BC = API_PLANE_TRAN SS <bc_id> <float1>

Description / Usage¶

(WIC/SCALAR ACOUS_PIMAG)

This boundary condition card applies the plane wave transmission conditions to the acoustic wave equations. This card concerns the imaginary part while APR_PLANE_TRAN concerns the real component. This condition is used to set reflection/transmission conditions for a surrounded material that is not being meshed. Definitions of the input parameters are as follows:

API_PLANE_TRAN: Name of the boundary condition (<bc_name>).
SS: Type of boundary condition (<bc_type>), where SS denotes side set in the EXODUS II database.
<bc_id>: The boundary flag identifier, an integer associated with <bc_type> that identifies the boundary location (side set in EXODUS II) in the problem domain.
<float1>: \(R_2\), the acoustic impedance (i.e. product of density and wave speed) in the surrounded material.

Examples¶

Following is a sample card:

BC = API_PLANE_TRAN SS 10 0.1

Technical Discussion¶

This condition should be used to account for transmission/reflection conditions for the external boundaries when the acoustic wave equation is used. It reflects characteristics for an acoustic wave encountering a planar interface between two materials;

where k is the acoustic wavenumber and R is the acoustic impedance. The subscript 1 refers to the material inside the external boundary and is the material which is meshed. Subscript 2 refers to the material outside of the external boundary. If \(R_2\) is set equal to \(R_1\), then this condition mimics an infinite boundary condition, i.e. no reflection at the external boundary.

END OF BC¶

END OF BC

Description / Usage¶

This card specifies the end of the list of boundary conditions (BCs), and is only used when automatic BC counting is used, as described in the Number of BC card. If the value of <integer> in that card is set to -1, all BC cards below the END of BC card are ignored, and Goma counts the number of BC cards between the Number of BC card and the END of BC card.

Examples¶

There are no input parameters for this card, which always appears as follows:

END OF BC