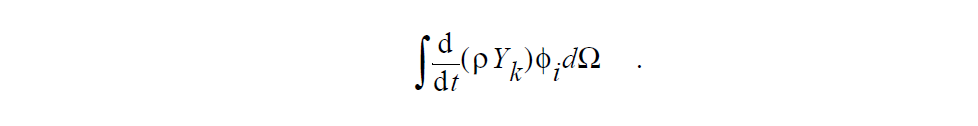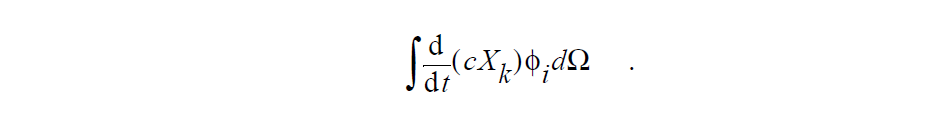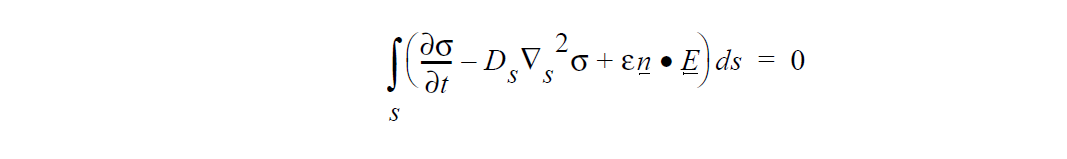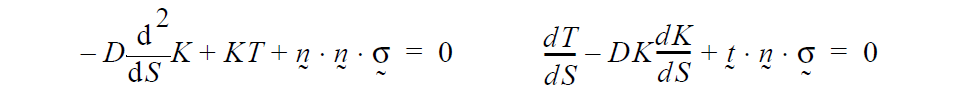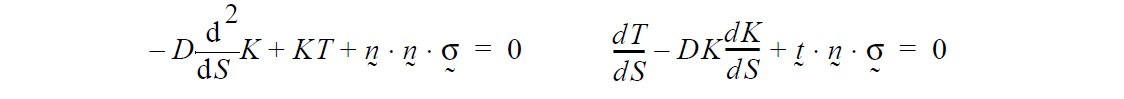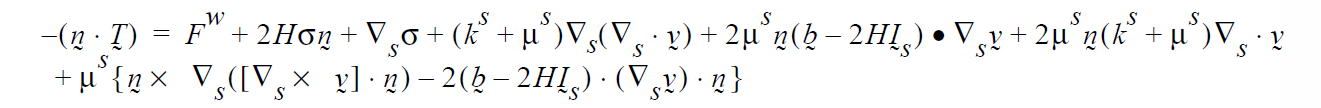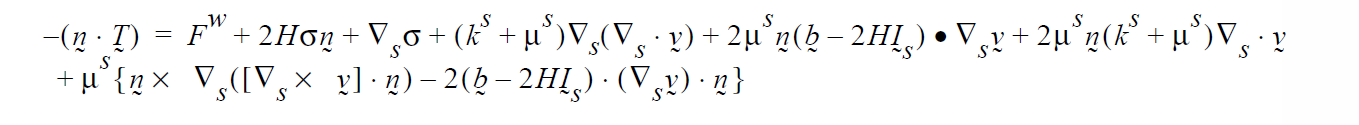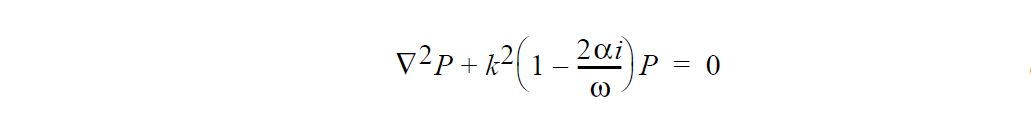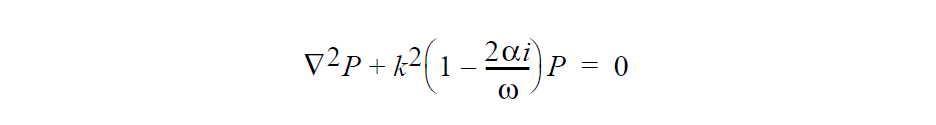Problem Description¶
This section directs all input specifications required for differential equations, material type, mesh motion type, coordinate system, finite element basis function type, and several other input tasks. This section of input records, with the exception of the Number of Materials card (the first one below), must be repeated for each material region in the problem. Within that region of the problem domain (and the corresponding section of the input file) there are no restrictions as to which differential or constraint equations can be specified, which is a unique capability of Goma.
However, some combinations or specifications do not make much sense, e.g., a cylindrical coordinate region combined with a cartesian one. It is recommended that the user consult the usage tutorials and example problems to get a feel for how this section is constructed.
Number of Materials¶
Number of Materials = <integer>
Description / Usage¶
This required card denotes how many material sections are contained in the Problem Description File. Each material section will have its own problem description, consisting of the following: MAT card, Coordinate System card, Mesh Motion card, Number of bulk species card, Number of EQ card, and zero or more equation cards. The input parameter is defined as
<integer> |
The number of MAT cards (i.e., material sections) that follow; this number must be greater than zero. |
If there are more MAT cards than specified by <integer>, Goma ignores all extras (i.e., the first Number of Materials material sections are read). If <integer> is set to -1, Goma automatically counts the MAT cards between the Number of Materials card and the END OF MAT card.
Examples¶
Following is a sample card, indicating that there are two materials:
Number of Materials = 2
Technical Discussion¶
No Discussion.
References¶
No References.
MAT¶
MAT = <char_string> <integer_list>
Description / Usage¶
This card represents the start of each material section in the Problem Description File. Thus, one MAT card is required for each material section. Definition of the input parameters are as follows:
<char_string> |
Filename of the material file from which all material properties for the current material will be read. The material file’s name plus extension is char_string.mat, and if the file is not present in the current working directory, the code will exit with the error message “Not all Material Files found in current directory.” |
<integer_list> |
This is a list of space delimited integers that define the set of element blocks for which this material file is applicable; the integers are the element block ids defined when the domain was meshed. |
Examples¶
The following specifies material file “sample.mat” applies to element blocks 1, 2, 3, 7, and 9:
MAT = sample 1 2 3 7 9
Note, the “.mat” extension is not specified explicitly, but appended to the character string by the code.
Technical Discussion¶
No Discussion.
References¶
No References.
Coordinate System¶
Coordinate System = {char_string}
Description / Usage¶
This card is required for each material section in the Problem Description File. It is used to specify formulation of the equations to be solved. Valid options for {char_string} are as follows:
CARTESIAN |
For a two (x-y) or three (x-y-z) dimensional Cartesian formulation. |
CYLINDRICAL |
For an axisymmetric (z-r) or three-dimensional cylindrical (z-r-\(\theta\)) formulation; the three-dimensional option has not been tested. |
SPHERICAL |
For a spherical (r-\(\theta\)-\(\phi\)) formulation. |
SWIRLING |
For a two-dimensional formulation (z-r-\(\theta\)) with a swirling velocity component that is independent of azimuthal coordinate. |
PROJECTED_CARTESIAN |
For use in the analysis of the three-dimensional stability of a two-dimensional flow field. The formulation (x-yz) has a z-velocity component that is independent of the z-direction. |
Examples¶
The following is a sample card that sets the coordinate system to Cartesian:
Coordinate System = CARTESIAN
Technical Discussion¶
Note the coordinate ordering for the CYLINDRICAL and SWIRLING options where the z-direction is first followed by the r-component (which in lay terms means the modeled region/part will appear to be ”lying down.”) If the SWIRLING option is activated, Goma expects a third momentum equation for the \(\theta\)-direction, i.e. EQ = momentum3, as explained in the equation section. The third component is basically the azimuthal \(\theta\)-velocity component, and the appropriate boundary conditions must be applied, e.g., on the w-component as described in the Category 4 boundary conditions for Fluid Momentum Equations.
References¶
No References.
Element Mapping¶
Element Mapping = <char_string>
Description / Usage¶
This card allows the user to set the order of the finite element shape mapping between the canonical element and each physical element. Valid options for {char_string} are:
isoparametric |
This choice sets the element order mapping to the highest order present in the problem. However, if a mesh displacement field is present, the element mapping order is the interpolation order of the mesh displacement field. |
Q1 |
This choice sets the element mapping order to bilinear. |
Q2 |
This choice sets the element mapping order to biquadratic. |
SP |
This choice sets the element mapping to order to subparametric. |
Technical Discussion¶
No Discussion.
References¶
No References.
Mesh Motion¶
Mesh Motion = {char_string}
Description / Usage¶
This card is required for each material section in the Problem Description File even if a moving mesh problem is not being solved. It is used to specify the method which prescribes the movement of nodes within the mesh. Valid options for {char_string} are:
ARBITRARY |
This option triggers the implicit pseudo-solid domainmapping technique using the constitutive equation designated in the corresponding file.mat (see Material File description); with this technique, the boundaries of the domain are controlled by distinguishing conditions coupled with the problem physics, and the interior nodes move independently of the problem physics. |
LAGRANGIAN |
This option triggers coupling the motion of nodes on the interior of the domain to the deformation of an elastic solid. If the solid is incompressible, this technique uses a pressure (Lagrange multiplier) to couple the solid deformation and the local solvent concentration. |
DYNAMIC_LAGRANGIAN |
This option triggers coupling the motion of nodes on the interior of the domain to the deformation of an elastic solid, including solid inertia. If the solid is incompressible, this technique uses a pressure (Lagrange multiplier) to couple the solid deformation and the local solvent concentration. Together with the equation term multiplier on the mass matrix (see EQ card) and a “transient” specification on the Time Integration Card, this option will invoke a Newmark- Beta time integration scheme for the inertia term in the R_MESH equations. |
TOTAL_ALE |
This option allows motion of nodes on the interior of the domain of a solid region to be independent of the material motion. TALE is an acronym for “Total Arbitrary Lagrangian Eulerian” mesh motion. This is typically used in elastic solids in which large scale deformation makes motions under the LAGRANGIAN option unmanageable. If the solid is incompressible, this technique uses a pressure (Lagrange multiplier) to couple the solid deformation and the local solvent concentration. Invoking this option requires mesh equations and real solid equations, as described on the EQ card. Other relevant cards that are often used with this option are KINEMATIC_DISPLACEMENT boundary condition, DX_RS, DY_RS, DZ_RS boundary conditions, FORCE_RS, FLUID_SOLID_RS, and others. See references for more detailed usage procedures. |
Examples¶
The following is a sample card that sets the mesh motion scheme to be arbitrary:
Mesh Motion = ARBITRARY
Technical Discussion¶
For the TOTAL_ALE mesh motion option we must supply elastic properties and solid constitutive equations for both the mesh and the real solid. It is best to consult the example tutorials cited below for details.
References¶
GT-005.3: THE NEW TOTAL-ARBITRARY-LAGRANGIAN-EULERIAN (TALE) CAPABILITY and its applicability to coating with/on deformable media, August 6, 1999, P. R. Schunk
GT-006.3: Slot and Roll coating with remeshing templates and tutorial for GOMA and CUBIT/MAPVAR, August 3, 1999, R. R. Lober and P. R. Schunk
Number of Bulk Species¶
Number of bulk species = <integer>
Description / Usage¶
This card is required for each material section in the Problem Description File. It is used to specify the number of species in a phase. The word, bulk, here, refers to its being distributed throughout the domain, not just at a surface. All loops over property evaluations use this value to specify the length of the loop. The single input parameter is defined as:
<integer> |
The number of species. If the value of <integer> is 0, then no species equations are solved for. |
In the absence of any further cards specifying the number of species equations, the number of species equations is set equal to the integer value supplied by this card, and there is an implied additional species, i.e., the solute, which is not part of species loops, but which fills out the specification of the phase.
Technical Discussion¶
Unfortunately, in the past, this card has specified the number of species equations instead of the number of species, as its name would imply! Now, the preferred treatment is to specify unequivocally both the number of bulk species and the number of bulk species equations using two separate input cards. If the two values are the same, then the system is semantically referred to as being “dilute” (even though it might not be!), and there is an inferred solute which is not part of the loop over species unknowns in property evaluations or even in the specification of properties in the .mat file. If the number of species is one greater than the number of species equations, then the system is deemed “nondilute” and the length of loops over property evaluations is one greater than the number of species equations. For nondilute systems, an equation of state must be implicitly used within Goma to solve for the value of the species unknown variable for the last species.
References¶
No References.
Material is Nondilute¶
Material is nondilute = {yes | no}
Description / Usage¶
This card is a optional for each material section in the Problem Description File. It is used to specify the number of species equations in a phase. The single string parameter is a boolean, yes or no.
yes |
the number of species equations is set equal to one less than the number of species. |
no |
the number of species equations is set equal to the number of species. |
When the number of species is equal to the number of species equations, there is an implied additional species, i.e., the solute, which is not part of species loops, which fills out the specification of the phase.
Technical Discussion¶
See the discussion for the “Number of bulk species” card.
References¶
No References.
Number of Bulk Species Equations¶
Number of bulk species equations = <integer>
Description / Usage¶
This card is optional but strongly recommended for each material section in the Problem Description File. It is used to specify the number of species equations in a phase. The word, bulk, here, refers to its being distributed throughout the domain, not just at a surface. The single input parameter is defined as:
<integer> |
The number of species equations; if the value of <integer> is 0, then no conservation equations for species are solved for. |
When the number of species is equal to the number of species equations, there is an implied additional species, i.e., the solute, which is not part of species loops, which fills out the specification of the phase.
Technical Discussion¶
See the discussion for the “Number of bulk species” card.
References¶
No References.
Default Material Species Type¶
Default Material Species Type = {species_type_string}
Description / Usage¶
This optional parameter sets the form of the species variable type within Goma. Valid options for {species_type_string} are given below by the SPECIES_* names (along with a description and variable (prefix) name:
SPECIES_MASS_FRACTION |
Mass Fractions |
Yk_ |
SPECIES_MOLE_FRACTION |
Mole Fractions |
Xk_ |
SPECIES_VOL_FRACTION |
Volume Fractions |
Vk_ |
SPECIES_DENSITY |
Species Densities |
Dk_ |
SPECIES_CONCENTRATION |
Species Concentration |
Ck_ |
SPECIES_UNDEFINED_FORM |
Undefined form |
Y |
The default is to assume SPECIES_UNDEFINED_FORM. Please refer to the Technical Discussion for important details.
Technical Discussion¶
For nondilute systems the SPECIES_ quantities above are not just simply interchangeable via a multiplicative constant. Their values are distinct, and their interrelationship evaluated via a potentially nontrivial equation of state. Prior to the implementation of this card/capability, Goma hadn’t handled many nondilute cases, and where it had, this issue was finessed by special casing property evaluations.
This card both sets the type of the species variables and establishes a convention for the units of equations within Goma. For settings of SPECIES_MASS_FRACTION and SPECIES_DENSITY_FRACTION, equations generally have a mass unit attached to them. Equations have concentration units attached to them for settings of SPECIES_MOLE_FRACTION, SPECIES_VOL_FRACTION, and SPECIES_CONCENTRATION. For example, given a setting of SPECIES_MASS_FRACTION, each volumetric term in the species conservation equation has units of mass per time, i.e., the time derivative term is written as
For a setting of SPECIES_MOLE_FRACTION, each volumetric term would have units of moles per time, i.e., the time derivative term is written out as
All this is necessary in order to handle cases where the total density or total concentration of a phase is spatially variable. In that case, it can’t just be divided out as in earlier versions of Goma but must be included in the conservation equations, and therefore the units of the conservation equation must reflect this.
The species variable type affects the units and thus values of quantities returned from certain boundary conditions. For example, the IS_EQUIL_PSEUDORXN boundary condition returns units of moles per time per \(length^2\) if the species variable type is defined to be SPECIES_CONCENTRATION, but will multiply by molecular weights and thus return units of mass per time per \(length^2\) if the species variable type is defined to be SPECIES_MASS_FRACTION. This change conforms to the expected units of the overall species conservation equation for the two values of the species variable type variable used as examples above.
The last column in the table above contains a three letter string. This string is used as a prefix for the name of the species variable in the EXODUS output file. If no names are specified in the material file and Chemkin is not used (which provides names for the species variables itself), then integers are used for names. For example, the first species unknown in Goma problem employing Mass Fractions as the independent species variables will be called Yk_1. If Chemkin is used in the same problem and the first chemkin species is named H2O, then the name in the EXODUS output file will be Yk_H2O. If a Goma problem is solved with no specification of the type of the species variable, then the first unknown in the EXODUS file will be named Y1.
Additionally, some boundary conditions and inputs from the material file section will set the species variable type on their own without the benefit of this card, if the species variable type is the default undefined form. Some internal checks are done; if an inconsistency is caught, Goma will abort with an informative error message.
Number of Viscoelastic Modes¶
Number of viscoelastic modes = <integer>
Description / Usage¶
This card is required only if you are performing a viscoelastic simulation and have included stress equations in the equation section and chosen a viscoelastic constitutive equation in the material file. The integer value denotes how many viscoelastic tensor stress equations are to be used. The number of modes can vary from a minimum of 1 to a maximum of 8. The input parameter is defined as
<integer> |
The number of viscoelastic modes, which must be greater than zero, but less than nine. |
Examples¶
The following is a sample card, indicating that a calculation with two viscoelastic stress modes is being undertaken:
Number of viscoelastic modes = 2
Technical Discussion¶
No Discussion.
References¶
Please see the viscoelastic tutorial memo for a discussion of multimode viscoelastic equations:
GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao
Number of EQ¶
Number of EQ = <integer>
Description / Usage¶
This card is required for each material section in the Problem Description File. It specifies how many equations (i.e., equation cards, [EQ =]) follow for this material section, including the mesh motion equations if appropriate. This number of equations is only for the current material, since each material has its own equation section.
The single input parameter is defined as
<integer> |
The number of EQ cards following this card. Only the first Number of EQ equations are read; if there are more EQ cards than specified by <integer>, Goma ignores the extras. If <integer> is set to -1, Goma will automatically count the number of EQ cards between the Number of EQ card and the END OF EQ card. |
Technical Discussion¶
For equation specification in Goma, it is important to remember that a scalar equation has a single equation entry (e.g. fill, species, voltage, shear rate, etc.), while a vector equation (e.g. momentum, mesh, mom_solid, etc.) has an entry for each component of the vector. Thus, if you were solving a two-dimension flow problem, you would need to specify both U1 and U2 components of the momentum equation explicitly. The same holds true for tensor equations (e.g. stress and velocity gradient); each term of the tensor is specified explicitly. The one exception to this rule is for multimode viscoelasticity where the first mode equations are specified through the equation card and then the auxiliary modes are set by the Number of viscoelastic modes card. Please see the viscoelastic tutorial memo (Rao, 2000) for a detailed discussion of multimode viscoelasticity.
References¶
GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao
Equation Cards
Following the Number of EQ card, the equation cards, or records, are racked as intended up to the *END OF EQ card or to the number specified, with one equation record per line. Each card begins with the “EQ =” string, followed by the equation name, e.g., energy, some basis function and trial function information, and finally a series of term multipliers. These multipliers are intended to provide a means of activating or deactivating terms of an equation, and hence should be set to zero or one. However, one can use these multipliers as a way of adjusting the scaling of individual terms. Exercise caution in using these factors as expedients for transport coefficients; for instance the equation term multiplier for the momentum diffusion term affects both the isotropic stress term (pressure) and the deviatoric stress. It is recommended that you consult the example tutorial menus and problems to get a feel for the structure of this section. A sample input file structure including the EQ section is shown in the figure at the beginning of this chapter.
energy¶
EQ = energy {Galerkin_wt} T {Interpol_fnc} <floatlist>
Description / Usage¶
This card provides information for solving a conservation of energy differential equation. Definitions of the input parameters are defined below. Note that <floatlist> contains five constants for the Energy equation defining the constant multipliers for each term in the equation. The Galerkin weight and the interpolation function must be the same for the code to work properly. If upwinding is desired for advection dominated problems, we can set this through a Petrov-Galerkin weight function in the material file.
energy |
Name of the equation to be solved. |
{Galerkin_wt} |
Two- or four-character value that defines the type of weighting function for this equation, where:
|
T |
Name of the variable associated with this equation. |
{Interpol_fnc} |
Two- or four-character value that defines the interpolation function used to represent the variable T, where:
|
<float1> |
Multiplier on mass matrix term ( d ⁄dt ). |
<float2> |
Multiplier on advective term. |
<float3> |
Multiplier on boundary term ( \(\underline{n}\) • flux ). |
<float4> |
Multiplier on diffusion term. |
<float5> |
Multiplier on source term. |
Note: These multipliers are intended to provide a means of activating or deactivating terms of an equation, and hence should be set to zero or one. If a multiplier is zero, the section of code that evaluates the corresponding term will be skipped.
Examples¶
The following is a sample card that uses a linear continuous interpolation and weight function and has all the term multipliers on except the mass matrix term for time derivatives:
EQ = energy Q1 T Q1 0. 1. 1. 1. 1.
Technical Discussion¶
Some discussion on the XFEM-type enriched basis functions Q1_XV, Q1_GN, Q1_GP, Q2_GN, Q2_GP and Q2_XV is in order. First of all, these basis functions are to be use with the level-set front tracking capability only. First of all, these basis functions are typically only used for the continuity equation to capture pressure jumps due to surface tension. However, for phase change problems some experimentation has been pursued with the energy equation.
XFEM Value Enrichment
Enrichment:
Related “Ghost” Enrichment:
Advantages:
This enrichment function allows discontinuity in value and gradient along interface but maintains continuity at element edges/faces. Appears to be method of choice for Pressure discontinuity. Produces interface integral for terms integrated by parts that allows for specifying a weak integrated conditions. This is needed in the laser welding heat transfer problem.
momentum¶
EQ = momentum{1|2|3} {Galerkin_wt} {U1|U2|U3} {Interpol_fnc} <floatlist>
Description / Usage¶
This card provides information for solving a differential equation for one component of a vector momentum equation. Definitions of the input parameters are defined below. Note that <floatlist> contains six constants for the Momentum equation defining the constant multipliers for each type of term in the equation. The Galerkin weight and the interpolation function must be the same for the code to work properly.
momentum1 | momentum2 | momentum3 |
Name of the equation to be solved, where the 1,2 and 3 components correspond to one of the principal coordinate directions, e.g. X, Y and Z for Cartesian geometry. |
{Galerkin_wt} |
Two- or four-character value that defines the type of weighting function for this equation, where:
|
U1 | U2 | U3 |
Name of the variable associated with the 1, 2 or 3 principal coordinate direction for this component equation. |
{Interpol_fnc} |
Two- or four-character value that defines the interpolation function used to represent the variable U1, U2 or U3 where:
|
<float1> |
Multiplier on mass matrix term ( d ⁄dt ). |
<float2> |
Multiplier on advective term. |
<float3> |
Multiplier on boundary term ( \(\underline{n}\) • flux ). |
<float4> |
Multiplier on diffusion term. |
<float5> |
Multiplier on source term. |
<float6> |
Multiplier on porous term (linear source). |
Note: These multipliers are intended to provide a means of activating or deactivating terms of an equation, and hence should be set to zero or one. If a multiplier is zero, the section of code that evaluates the corresponding term will be skipped.
Examples¶
The following is a sample card that uses quadratic continuous velocity interpolation and weight function and turns on all equation term multipliers except for the mass matrix and the porous term:
EQ = momentum1 Q2 U1 Q2 0. 1. 1. 1. 1. 0.
Technical Discussion¶
No Discussion.
References¶
No References.
pmomentum¶
EQ = pmomentum{1|2|3} {Galerkin_wt} {PU1|PU2|PU3} {Interpol_fnc}<floatlist>
Description / Usage¶
This card provides information for solving a differential equation for one component of a vector particle momentum equation. Definitions of the input parameters are defined below. Note that <floatlist> contains six constants for the Pmomentum equation defining the constant multipliers for each type of term in the equation. The Galerkin weight and the interpolation function must be the same for the code to work properly.
pmomentum1 | pmomentum2 | pmomentum3 |
Name of the equation to be solved, where the 1, 2 and 3 components correspond to one of the principal coordinate directions, e.g. X, Y and Z for Cartesian geometry. |
{Galerkin_wt} |
Two- or four-character value that defines the type of weighting function for this equation, where:
|
PU1 | PU2 | PU3 |
Name of the variable associated with the 1, 2 or 3 principal coordinate direction for this component equation. |
{Interpol_fnc} |
Two- or four-character value that defines the interpolation function used to represent the variable PU1, PU2 or PU3 where:
|
<float1> |
Multiplier on mass matrix term ( d ⁄dt ). |
<float2> |
Multiplier on advective term. |
<float3> |
Multiplier on boundary term ( \(\underline{n}\) • flux ). |
<float4> |
Multiplier on diffusion term. |
<float5> |
Multiplier on source term. |
<float6> |
Multiplier on porous term (linear source). |
Note: These multipliers are intended to provide a means of activating or deactivating terms of an equation, and hence should be set to zero or one. If a multiplier is zero, the section of code that evaluates the corresponding term will be skipped.
Examples¶
The following is a sample card that uses quadratic continuous velocity interpolation and weight function and turns on all equation term multipliers except for the mass matrix and the porous term:
EQ = momentum1 Q2 PU1 Q2 0. 1. 1. 1. 1. 0.
Technical Discussion¶
The particle momentum equations have been added to Goma as part of a research project and are not currently in use for production computing.
References¶
No References.
stress¶
EQ = {eqname} {Galerkin_wt} {varname} {Interpol_fnc} <floatlist>
Description / Usage¶
This card provides information for solving a differential equation. Definitions of the input parameters are defined below. Note that <floatlist> contains five constants for the Stress equation defining the constant multipliers for each type of term in the equation. The Galerkin weight and the interpolation function must be the same for the code to work properly. If upwinding is desired for advection dominated problems, we can set this through a Petrov-Galerkin weight function in the material file.
{eqname} |
The name of the component of the stress equation to be solved, one of the following: stress11, stress12, stress13, stress22, stress23, stress33. |
{Galerkin_wt} |
Two-character or three-character value that defines the type of weighting function for this equation, where:
|
{varname} |
The name of the variable associated with the respective components (11, 12, 13, 22, 23, and 33) of the symmetric Stress tensor, which are S11, S12, S13, S22, S23, S33. |
{Interpol_fnc} |
Two-character or three-character value that defines the interpolation function used to represent the variable S11, S12, S13, S22, S23 or S33, where:
|
<float1> |
Multiplier on mass matrix term ( d ⁄dt ). |
<float2> |
Multiplier on advective term. |
<float3> |
Multiplier on boundary term ( \(\underline{n}\) • flux ). |
<float4> |
Multiplier on diffusion term. |
<float5> |
Multiplier on source term. |
Note: These multipliers are intended to provide a means of activating or deactivating terms of an equation, and hence should be set to zero or one. If a multiplier is zero, the section of code that evaluates the corresponding term will be skipped.
Examples¶
The following is a sample card that uses a linear continuous interpolation for stress and turns on all the term multipliers:
EQ = stress11 Q1 S11 Q1 1. 1. 1. 1. 1.
Technical Discussion¶
The interpolation/weight functions that are discontinuous, e.g. have the prefix “P”, invoke the discontinuous Galerkin method for solving the stress equations where the interpolation is discontinuous and flux continuity is maintained by performing surface integrals. For details of the implementation of the discontinuous Galerkin method in Goma please see the viscoelastic tutorial memo (Rao, 2000).
References¶
GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao
species_bulk¶
EQ = species_bulk {Galerkin_wt} Y {Interpol_fnc} <floatlist>
Description / Usage¶
This card provides information for solving a differential equation. Definitions of the input parameters are defined below. Note that <floatlist> contains five parameters to define the constant multipliers in front of each type of term in the equation. The Galerkin weight and the interpolation function must be the same for the code to work properly. If upwinding is desired for advection dominated problems, we can set this through a Petrov-Galerkin weight function in the material file.
species_bulk |
Name of the equation to be solved. This equation type should only be listed once regardless of the number of species (the Number of bulk species card specifies the number of species_bulk equations to be solved). Differences in diffusion coefficients between species should be accounted for in the materials properties section of Goma. |
{Galerkin_wt} |
Two- to four-character value that defines the type of weighting function for this equation, where:
|
Y |
Name of the variable associated with this equation. |
{Interpol_fnc} |
Two- to four-character value that defines the interpolation function used to represent the variable Y, where:
|
<float1> |
Multiplier on mass matrix term ( d ⁄dt ). |
<float2> |
Multiplier on advective term. |
<float3> |
Multiplier on boundary term ( \(\underline{n}\) • flux ). |
<float4> |
Multiplier on diffusion term. |
<float5> |
Multiplier on source term. |
Note: These multipliers are intended to provide a means of activating or deactivating terms of an equation, and hence should be set to zero or one. If a multiplier is zero, the section of code that evaluates the corresponding term will be skipped.
Examples¶
The following is a sample card that uses quadratic continuous interpolation for the species equation and turns on all the term multipliers:
EQ = species_bulk Q2 Y Q2 1. 1. 1. 1. 1.
Technical Discussion¶
The interpolation/weight functions that are discontinuous, e.g. have the prefix “P”, invoke the discontinuous Galerkin (DG) method for solving the species equations where the interpolation is discontinuous and flux continuity is maintained by performing surface integrals. For details of the implementation of the DG method in Goma please see the viscoelastic tutorial memo. Note, the DG implementation for the species equation is only for advection dominated problems; DG methods have not yet been completely developed for diffusion operators.
Also, please see EQ=energy input for more detailed description of the Q1_GN, Q2_GN, Q1_GP, Q2_GP, Q1_XV and Q2_XV enriched basis functions.
References¶
GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao
mesh¶
EQ = mesh{1|2|3} {Galerkin_wt} {D1|D2|D3} {Interpol_fnc} <floatlist}
Description / Usage¶
This card provides information for solving a differential equation for one component of mesh motion. Definitions of the input parameters are defined below. Note that <floatlist> contains five constants for the Mesh equation defining the constant multipliers for each type of term in the equation. The Galerkin weight and the interpolation function must be the same for the code to work properly.
mesh1 | mesh2 | mesh3 |
Name of the equation to be solved, where the 1, 2 and 3 components correspond to one of the principal coordinate directions, e.g. X, Y and Z for Cartesian geometry. |
{Galerkin_wt} |
Two-character value that defines the weighting function type for this equation, where:
|
D1 | D2 | D3 |
Name of the variable associated with the 1, 2 or 3 principal coordinate direction for this component equation. |
{Interpol_fnc} |
Two-character value that defines the interpolation function used to represent the variable D1, D2 or D3 where:
|
<float1> |
Multiplier on mass matrix term ( d ⁄dt ). |
<float2> |
Multiplier on advective term. |
<float3> |
Multiplier on boundary term ( \(\underline{n}\) • flux ). |
<float4> |
Multiplier on diffusion term. |
<float5> |
Multiplier on source term. |
Note: These multipliers are intended to provide a means of activating or deactivating terms of an equation, and hence should be set to zero or one. If a multiplier is zero, the section of code that evaluates the corresponding term will be skipped.
Examples¶
The following is a sample card for the first mesh equation that uses linear continuous interpolation and turns on all term multipliers except for the mass matrix:
EQ = mesh1 Q1 D1 Q1 0. 1. 1. 1. 1.
Technical Discussion¶
No Discussion.
References¶
No References.
mom_solid¶
EQ = mom_solid{1|2|3} {Galerkin_wt} {D1|D2|D3}_RS {Interpol_fnc} <floatlist>
Description / Usage¶
This card provides information for solving a differential equation for one component of a solid momentum equation. Definitions of the input parameters are defined below. Note that <floatlist> contains five constants for the Solid Momentum equation defining the constant multipliers for each type of term in the equation. The Galerkin weight and the interpolation function must be the same for the code to work properly.
mom_solid1 | mom_solid2 | mom_solid3 |
Name of the equation to be solved, where the 1, 2 and 3 components correspond to one of the principal coordinate directions, e.g. X, Y and Z for Cartesian geometry. |
{Galerkin_wt} |
Two-character value that defines the type of weighting function for this equation, where:
|
D1_RS | D2_RS | D3_RS |
Name of the variable associated with the 1, 2 or 3 principal coordinate direction for this component equation. |
{Interpol_fnc} |
Two-character value that defines the interpolation function used to represent the variable D1_RS, D2_RS or D3_RS where:
|
<float1> |
Multiplier on mass matrix term ( d ⁄dt ). |
<float2> |
Multiplier on advective term. |
<float3> |
Multiplier on boundary term ( \(\underline{n}\) • flux ). |
<float4> |
Multiplier on diffusion term. |
<float5> |
Multiplier on source term. |
Note: These multipliers are intended to provide a means of activating or deactivating terms of an equation, and hence should be set to zero or one. If a multiplier is zero, the section of code that evaluates the corresponding term will be skipped.
Examples¶
The following is a sample card for the first solid mesh equation that uses linear continuous interpolation and turns on all term multipliers except for the mass matrix:
EQ = mom_solid1 Q1 D1_RS Q1 0. 1. 1. 1. 1.
Technical Discussion¶
The solid momentum equations are used as a second set of displacement equations when the ALE (arbitrary-Lagrangian Eulerian) technique is used in the solid phase as well as the liquid phase. We have termed this capability TALE for “total arbitraryd Lagrangian Eulerian” and details of implementation and usage for Goma can be found in Schunk (2000).
References¶
SAND2000-0807: TALE: An Arbitrary Lagrangian-Eulerian Approach to Fluid- Structure Interaction Problems, P. R. Schunk (May 2000)
continuity¶
EQ = continuity {Galerkin_wt} P {Interpol_fnc} <float1> <float2>
Description / Usage¶
This card provides information for solving a differential equation. Definitions of the input parameters are defined below. Note that <float1> and <float2> define the constant multipliers for each type of term in the Continuity equation. The Galerkin weight and the interpolation function must be the same for the code to work properly.
continuity |
Name of the equation to be solved. |
{Galerkin_wt} |
Two-character value that defines the type of weighting function for this equation, where:
|
P |
Name of the variable (pressure) associated with this equation. |
{Interpol_fnc} |
Two-character value that defines the interpolation function used to represent the variable P, where:
|
<float1> |
Multiplier on divergence term. |
<float2> |
Multiplier on source term. This multiplier is equal to the initial volume fraction of solvents for Lagrangian mesh motion with swelling. |
Note: These multipliers are intended to provide a means of activating or deactivating terms of an equation, and hence should be set to zero or one. If a multiplier is zero, the section of code that evaluates the corresponding term will be skipped.
Examples¶
The following is a sample card that uses a constant discontinuous pressure interpolation and weight function and turns on both the divergence and source terms.
EQ = continuity P0 P P0 1. 1.
Technical Discussion¶
Please see the EQ=energy equation card for a more detailed description of P0_XV, P1_XV, Q1_XV, Q2_XV interpolations. These are MOST COMMONLY used for the continuity equation for better accuracy of representing pressure across level-set interfaces with surface tension.
References¶
No References.
fill¶
EQ = fill {Galerkin_wt} F {Interpol_fnc} <float1> <float2> <float3>
Description / Usage¶
This card provides information for solving a differential equation for the fill equation. Definitions of the input parameters are defined below. Note that <float1> through <float3> define the constant multipliers for each term in the equation. The Galerkin weight and the interpolation function must be the same for the code to work properly.
fill |
Name of the equation to be solved. |
{Galerkin_wt} |
Two-character value that defines the type of weighting function for this equation, where:
|
F |
Name of the variable associated with this equation. |
{Interpol_fnc} |
Two-character value that defines the interpolation function used to represent the variable F, where:
|
<float1> |
Multiplier on mass matrix term ( d ⁄dt ). |
<float2> |
Multiplier on advective term. |
<float3> |
Multiplier on source term. |
Examples¶
The following is a sample card that uses continuous linear interpolation for the fill equation:
EQ = fill Q1 F Q1 1. 1. 1.
Technical Discussion¶
The fill equation is used in the calculation of volume of fluid interface tracking. It solves an advection equation of a color function that takes on a different integer value depending on which fluid phase you are in. For most applications this capability has been superseded by the level set method of interface tracking.
The interpolation/weight functions that are discontinuous, e.g. have the prefix “P” invoke the discontinuous Galerkin (DG) method for solving the fill equations where the interpolation is discontinuous and flux continuity is maintained by evaluating surface integrals. For details of the implementation of the DG method in Goma please see the viscoelastic tutorial memo (Rao, 2000).
References¶
GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao
lagr_mult_1, lagr_mult_2, lagr_mult_3¶
EQ = lagr_mult_{1|2|3} {Galerkin_wt} LM{1|2|3} {Interpol_fnc}
Description / Usage¶
This card provides information for solving a Langrange multiplier vector equation for imposition of the kinematic boundary condition at a fluid/solid interface. It is used soley for the overset grid capability in Goma (cf. GT-026.2). Definitions of the input parameters are defined below. The Galerkin weight and the interpolation function must be the same for the code to work properly.
lagr_mult_1 | lagr_mult_2 | lagr_mult_3 |
Name of the equation to be solved. The appended number indexes with the dimension of the problem, viz. lagr_mult_1 and lagr_mult_2 equations are required for a two dimensional problem. |
{Galerkin_wt} |
Two-character value that defines the type of weighting function for this equation, where:
|
LM1 | LM2 | LM3 |
Name of the variable associated with this equation. |
{Interpol_fnc} |
Two-character value that defines the interpolation function used to represent the variable P, where:
|
Basically when the level-set field (actually phase field 1, cf. F1 equation) that corresponds to solid/fluid boundary defined by an overset grid (using the Slave Level Set Card) intersects an element, the equations associated with that element will get the kinematic boundary condition for the fluid-structure interaction, which basically equates the fluid velocity to the solid velocity. In elements that don’t contain the solid/ fluid boundary, the equations are trivialized so that they are condensed out of the system to be solved.
Examples¶
The following is a sample cards are required for the overset grid capability for twodimensional problems. It is recommended that P0 (element constant) interpolation functions be used.
EQ = lagr_mult_1 P0 LM1 P0 1
EQ = lagr_mult_2 P0 LM2 P0 1
Technical Discussion¶
No Discussion.
References¶
GT-026.3 GOMA’s Overset Mesh Method: User Tutorial. November 19, 2003. P. R. Schunk and E. D. Wilkes
level set¶
EQ = level set {Galerkin_wt} F {Interpol_fnc} <float1> <float2> <float3>
Description / Usage¶
This card provides information for solving a differential equation for the level set equation. Definitions of the input parameters are defined below. Note that <float1> through <float3> define the constant multipliers for each term in the equation. The Galerkin weight and the interpolation function must be the same for the code to work properly. If upwinding is desired, we can set this through a Petrov-Galerkin weight function in the level set section of the input file (Time Integration Specifications).
level set |
Name of the equation to be solved. |
{Galerkin_wt} |
Two-character value that defines the type of weighting function for this equation, where:
|
F |
Name of the variable associated with this equation. |
{Interpol_fnc} |
Two-character value that defines the interpolation function used to represent the variable F, where:
|
Examples¶
The following is a sample card that uses continuous linear interpolation for the level set equation and turns on all term multipliers:
EQ = level_set Q1 F Q1 1. 1. 1.
Technical Discussion¶
The interpolation/weight functions that are discontinuous, e.g. have the prefix “P”, invoke the discontinuous Galerkin (DG) method for solving the level set equations where the interpolation is discontinuous and flux continuity is maintained by evaluating surface integrals. For details of the implementation of the DG method in Goma please see the viscoelastic tutorial memo (Rao, 2000). Note that DG methods are not necessarily recommended for the level set equation since it is inherently smooth.
References¶
GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao
voltage¶
EQ = voltage {Galerkin_wt} V {Interpol_fnc} <floatlist>
Description / Usage¶
This card provides information for solving a differential equation for the voltage. Definitions of the input parameters are defined below. Note that <floatlist> has five parameters to define the constant multipliers in front of each type of term in the equation. The Galerkin weight and the interpolation function must be the same for the code to work properly.
voltage |
Name of the equation to be solved. |
{Galerkin_wt} |
Two-character value that defines the type of weighting function for this equation, where:
|
V |
Name of the variable associated with this equation. |
{Interpol_fnc} |
Two-character value that defines the interpolation function used to represent the variable V, where:
|
<float1> |
Multiplier on mass matrix term ( d ⁄dt ). |
<float2> |
Multiplier on advective term. |
<float3> |
Multiplier on boundary term ( \(\underline{n}\) • flux ). |
<float4> |
Multiplier on diffusion term. |
<float5> |
Multiplier on source term. |
Note: These multipliers are intended to provide a means of activating or deactivating terms of an equation, and hence should be set to zero or one. If a multiplier is zero, the section of code that evaluates the corresponding term will be skipped.
Examples¶
The following is a sample card that uses a linear interpolation function for voltage:
EQ = voltage Q1 V Q1 0. 1. 1. 1. 1.
Technical Discussion¶
The voltage equation has no mass term, viz. it is quasistatic. So it won’t matter whether that multiplier is 1 or 0.
References¶
No References.
efield¶
EQ = efield{1 | 2 | 3} {Galerkin_wt} {E1 | E2 | E3} {Interpol_fnc} <floatlist>
Description / Usage¶
This card provides information for solving a definition equation for the vector electric field, which is the gradient of the voltage or potential field (see voltage equation). Hence, these equations (two components in two dimensions, and three components in three dimensions) must be solved together with the voltage equation.
efield1 | efield2 | efield3 |
Name of the equation to be solved. |
{Galerkin_wt} |
Two-character value that defines the type of weighting function for this equation, where:
|
E1 | E2 | E3 |
Name of the variable associated with this equation. |
{Interpol_fnc} |
Two-character value that defines the interpolation function used to represent the variable E1, E2, or E3, where:
|
<float1> |
Multiplier on advective term. |
<float2> |
Multiplier on source term. |
Note: These multipliers are intended to provide a means of activating or deactivating terms of an equation, and hence should be set to zero or one. If a multiplier is zero, the section of code that evaluates the corresponding term will be skipped.
Examples¶
The following is an example of efield-equation specification using linear elements in two dimensions. Notice the companion voltage equation.
EQ = efield1 Q1 E1 Q1 1. 1.
EQ = efield2 Q1 E1 Q1 1. 1.
EQ = voltage Q1 V Q1 1. 1. 1. 1. 1. 1.
This set of equations is required for applying an electrohydrodynamic force to the fluid momentum equations (see Navier-Stokes Source card. )
Technical Discussion¶
The electric field is defined by \(\underline{E}\) = –\(\Delta\) \(\phi\). In some cases it may be more convenient to solve equations for the potential field and the electric field.
enorm¶
EQ = enorm {Galerkin_wt} ENORM {Interpol_fnc} <float1> <float2>
Description / Usage¶
This card provides information for solving a “dependency” equation for the norm of the electric field. Definitions of the input parameters are defined below. Note that <float1> and <float2> define the constant multipliers in front of each type of term in the equation. The Galerkin weight and the interpolation function must be the same for the code to work properly.
enorm |
Name of the equation to be solved. |
{Galerkin_wt} |
Two-character value that defines the type of weighting function for this equation, where:
|
ENORM |
Name of the variable associated with this equation. |
{Interpol_fnc} |
Two-character value that defines the interpolation function used to represent the variable ENORM, where:
|
<float1> |
Multiplier on advection term. |
<float2> |
Multiplier on source term. |
Note: These multipliers are intended to provide a means of activating or deactivating terms of an equation, and hence should be set to zero or one. If a multiplier is zero, the section of code that evaluates the corresponding term will be skipped. See below for important information regarding this.
Examples¶
The following is a sample card that uses quadratic continuous interpolation for the enorm equation and turns on all the term multipliers (the usual usage):
EQ = enorm Q2 ENORM Q2 1.0 1.0
Technical Discussion¶
This equation allows the user to use the variable ENORM, the norm of the electric field, which is equal to \(\mid\) \(\underline{E}\) \(\mid\), or \(\mid\) \(\underline \Delta\) V \(\mid\), with V being the voltage potential. As such, the VOLTAGE equation must be present. We refer to this as a “dependent” equation or “auxiliary” equation because, although it’s value can technically be derived from the V variable directly, we would lose derivative information by doing so. This equation is introduced solely so one can access higher derivatives of V than its interpolation would normally allow. For example, V if were interpolated with a linear basis, then \(\underline \Delta\) V would have a constant interpolant. If we wanted access to \(\underline \Delta\) (\(\underline \Delta\) V) , it would be zero! (In reality, we would use bilinear or trilinear basis functions, so this isn’t precisely true but it expresses the essential problem.) By introducing this primitive variable, we can retrieve useful values for \(\underline \Delta\).
The two term multipliers refer to the multiple on the assembled value of enorm (stored in the “advection” term–it has nothing to do with advection), and the multiple on the assembled value derived from the voltage equation (stored in the “source” term–again the name of the term is somewhat artificial).
References¶
No References.
shear_rate¶
EQ = shear_rate {Galerkin_wt} SH {Interpol_fnc} <float1> <float2> <float3>
Description / Usage¶
This card provides information for solving a differential equation for the scalar shear rate invariant. Definitions of the input parameters are defined below. Note that <float1> through <float3> define the constant multipliers in front of each type of term in the equation. The Galerkin weight and the interpolation function must be the same for the code to work properly.
shear_rate |
Name of the equation to be solved. |
{Galerkin_wt} |
Two-character value that defines the type of weighting function for this equation, where:
|
SH |
Name of the variable associated with this equation. |
{Interpol_fnc} |
Two-character value that defines the interpolation function used to represent the variable SH, where:
|
<float1> |
Multiplier on advective term. |
<float2> |
Multiplier on diffusion term. |
<float3> |
Multiplier on source term. |
Note: These multipliers are intended to provide a means of activating or deactivating terms of an equation, and hence should be set to zero or one. If a multiplier is zero, the section of code that evaluates the corresponding term will be skipped.
Examples¶
The following is a sample card that uses quadratic continuous interpolation for the species equation and turns on all the term multipliers:
EQ = shear_rate Q2 SH Q2 1. 1. 1.
Technical Discussion¶
No Discussion.
References¶
No References.
vort_dir¶
EQ = vort_dir{1|2|3} {Galerkin_wt} {VD1|VD2|VD3} {Interpol_fnc}
Description / Usage¶
This card provides information for solving a differential equation for one component of the vorticity equation. Definitions of the input parameters are defined below; there is no <float> input for this equation. The Galerkin weight and the interpolation function must be the same for the code to work properly.
vort_dir1 | vort_dir2 | vort_dir3 |
Name of the equation to be solved, where the 1, 2 and 3 components correspond to one of the principal coordinate directions, e.g. X, Y and Z for Cartesian geometry. |
{Galerkin_wt} |
Two–character value that defines the type of weighting function for this equation, where:
|
VD1 | VD2 | VD3 |
Name of the variable associated with the 1, 2 or 3 principal coordinate direction for this component equation. |
{Interpol_fnc} |
Two-character value that defines the interpolation function used to represent the variable VD1, VD2 or VD3, where:
|
Examples¶
The following is a sample card that uses a linear continuous interpolation and weight function:
EQ = vort_dir1 Q1 VD1 Q1
Technical Discussion¶
This equation type is used for a research capability involving the flows of suspensions in curvilinear coordinates and is not currently being used for production computations.
vort_lambda¶
EQ = vort_lambda {Galerkin_wt} VLAMBDA {Interpol_fnc}
Description / Usage¶
This card provides information for solving a differential equation for the vorticity direction. Definitions of the input parameters are defined below; there are no <float> input parameters for this equation. The Galerkin weight and the interpolation function must be the same for the code to work properly.
vort_lamda |
Name of the equation to be solved. |
{Galerkin_wt} |
Two-character value that defines the type of weighting function for this equation, where:
|
VLAMBDA |
Name of the variable associated with this equation. |
{Interpol_fnc} |
Two-character value that defines the interpolation function used to represent the variable VLAMBDA, where:
|
Examples¶
No Examples.
Technical Discussion¶
This equation type is used for a research capability involving the flows of suspensions in curvilinear coordinates and is not currently being used for production computations.
porous_sat¶
EQ = porous_sat {Galerkin_wt} P_liq {Interpol_fnc} <floatlist>
Description / Usage¶
This card provides information for solving a differential equation for saturated porous flow. Definitions of the input parameters are defined below. Note that <floatlist> has five parameters to define the constant multipliers in front of each type of term in the equation.The Galerkin weight and the interpolation function must be the same for the code to work properly. If upwinding is desired for advection dominated problems, we can set this through a Petrov-Galerkin weight function in the material file.
porous_sat |
Name of the equation to be solved. |
{Galerkin_wt} |
Two-character value that defines the type of weighting function for this equation, where:
|
P_SAT |
Name of the variable associated with this equation. |
{Interpol_fnc} |
Two-character value that defines the interpolation function used to represent the variable P_SAT, where:
|
<float1> |
Multiplier on mass matrix term ( d ⁄dt ). |
<float2> |
Multiplier on advective term. |
<float3> |
Multiplier on boundary term ( \(\underline{n}\) • flux ). |
<float4> |
Multiplier on diffusion term. |
<float5> |
Multiplier on source term. |
Note: These multipliers are intended to provide a means of activating or deactivating terms of an equation, and hence should be set to zero or one. If a multiplier is zero, the section of code that evaluates the corresponding term will be skipped.
Examples¶
The following is a sample card that uses a linear continuous interpolation and weight function for the saturated porous equation and has all the term multipliers on except for the mass matrix for time derivatives:
EQ = porous_sat Q1 P_liq Q1 0. 1. 1. 1. 1.
Technical Discussion¶
This card is not yet in use.
References¶
No References.
porous_unsat¶
EQ = porous_unsat {Galerkin_wt} P_LIQ {Interpol_fnc} <floatlist>
Description / Usage¶
This equation cannot be invoked in an element block in which the media type is set to POROUS_TWO_PHASE (cf. Microstructure Properties, Media Type card). Otherwise, it is used exactly as the porous_liq equation card; please consult that section for a detailed discussion.
See porous_liq card for description of input requirements.
Examples¶
See porous_liq card.
Technical Discussion¶
This card is used for single phase (viz. constant gas pressure) simulations of partially saturated flow, as described by the Media Type material property card. The equation it invokes is one of Darcy flow in a partially saturated medium in which the gas phase pressure is taken as constant. The dependent variable here is the liquid phase pressure.
References¶
GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk
GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk
porous_liq¶
EQ = porous_liq {Galerkin_wt} P_LIQ {Interpol_fnc} <floatlist>
Description / Usage¶
This card provides information for solving a differential equation for porous liquid phase pressure. This equation is of the exact same form as porous_unsat, but is required if two-phase simulations are to be made (cf. Miscrostructure Properties, Media Type card). This equation can be used for media types POROUS_UNSATURATED, POROUS_SATURATED, and POROUS_TWO_PHASE. Definitions of the input parameters are defined below. Note that <floatlist> contains five parameters to define the constant multipliers in front of each type of term in the equation. The Galerkin weight and the interpolation function must be the same for the code to work properly. If upwinding is desired for advection dominated problems, we can set this through a Petrov-Galerkin weight function in the material file.
porous_liq |
Name of the equation to be solved. |
{Galerkin_wt} |
Two-character value that defines the type of weighting function for this equation, where:
|
P_LIQ |
Name of the variable associated with this equation. |
{Interpol_fnc} |
Two-character value that defines the interpolation function used to represent the variable P_LIQ, where:
|
<float1> |
Multiplier on mass matrix term ( d ⁄dt ). |
<float2> |
Multiplier on advective term. |
<float3> |
Multiplier on boundary term ( \(\underline{n}\) • flux ). |
<float4> |
Multiplier on diffusion term. |
<float5> |
Multiplier on source term. |
Note: These multipliers are intended to provide a means of activating or deactivating terms of an equation, and hence should be set to zero or one. If a multiplier is zero, the section of code that evaluates the corresponding term will be skipped.
Examples¶
The following is a sample card that uses a linear continuous interpolation and weight function for the porous liquid phase pressure equation and has all the term multipliers on except for the mass matrix for time derivatives:
EQ = porous_liq Q1 P_LIQ Q1 0. 1. 1. 1. 1.
Technical Discussion¶
No Discussion.
References¶
GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk
GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk
porous_gas¶
EQ = porous_gas {Galerkin_wt} P_GAS {Interpol_fnc} <floatlist>
Description / Usage¶
This card provides information for solving a differential equation for porous gas phase pressure. Definitions of the input parameters are defined below. Note that <floatlist> has five parameters to define the constant multipliers in front of each type of term in the equation.The Galerkin weight and the interpolation function must be the same for the code to work properly. If upwinding is desired for advection dominated problems, we can set this through a Petrov-Galerkin weight function in the material file.
porous_gas |
Name of the equation to be solved. |
{Galerkin_wt} |
Two-character value that defines the type of weighting function for this equation, where:
|
P_GAS |
Name of the variable associated with this equation. |
{Interpol_fnc} |
Two-character value that defines the interpolation function used to represent the variable P_GAS, where:
|
<float1> |
Multiplier on mass matrix term ( d ⁄dt ). |
<float2> |
Multiplier on advective term. |
<float3> |
Multiplier on boundary term ( \(\underline{n}\) • flux ). |
<float4> |
Multiplier on diffusion term. |
<float5> |
Multiplier on source term. |
Note: These multipliers are intended to provide a means of activating or deactivating terms of an equation, and hence should be set to zero or one. If a multiplier is zero, the section of code that evaluates the corresponding term will be skipped.
Examples¶
The following is a sample card that uses a linear continuous interpolation and weight function for the porous gas phase pressure equation and has all the term multipliers on except for the mass matrix for time derivatives:
EQ = porous_gas Q1 P_GAS Q1 0. 1. 1. 1. 1.
Technical Discussion¶
No Discussion.
References¶
GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk
GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk
porous_deform¶
EQ = porous_deform {Galerkin_wt} P_POR {Interpol_fnc} <floatlist>
Description / Usage¶
This card provides information for solving a differential equation for porous solid phase porosity. Definitions of the input parameters are defined below. Note that <floatlist> has five parameters to define the constant multipliers in front of each type of term in the equation. The Galerkin weight and the interpolation function must be the same for the code to work properly. If upwinding is desired for advection dominated problems, we can set this through a Petrov-Galerkin weight function in the material file.
porous_deform |
Name of the equation to be solved. |
{Galerkin_wt} |
Two-character value that defines the type of weighting function for this equation, where:
|
P_POR |
Name of the variable associated with this equation. |
{Interpol_fnc} |
Two-character value that defines the interpolation function used to represent the variable P_POR, where:
|
<float1> |
Multiplier on mass matrix term ( d ⁄dt ). |
<float2> |
Multiplier on advective term. |
<float3> |
Multiplier on boundary term ( \(\underline{n}\) • flux ). |
<float4> |
Multiplier on diffusion term. |
<float5> |
Multiplier on source term. |
Note: These multipliers are intended to provide a means of activating or deactivating terms of an equation, and hence should be set to zero or one. If a multiplier is zero, the section of code that evaluates the corresponding term will be skipped.
Examples¶
The following is a sample card that uses a linear continuous interpolation and weight function for the deforming porous porosity equation and has all the term multipliers on except for the mass matrix for time derivatives:
EQ = porous_deform Q1 P_POR Q1 0. 1. 1. 1. 1.
Technical Discussion¶
No Discussion.
References¶
GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk
GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk
porous_energy¶
EQ = porous_energy {Galerkin_wt} P_TEMP {Interpol_fnc} <floatlist>
Description / Usage¶
This card provides information for solving a conservation of energy differential equation for porous media, deploying a multiphase formulation.. Definitions of the input parameters are defined below. Note that <floatlist> contains six constants for the porous energy equation defining the constant multipliers for each term in the equation. The Galerkin weight and the interpolation function must be the same for the code to work properly.
porous_energy |
Name of the equation to be solved. |
{Galerkin_wt} |
Two- or four-character value that defines the type of weighting function for this equation, where:
|
T |
Name of the variable associated with this equation. |
{Interpol_fnc} |
Two- or four-character value that defines the interpolation function used to represent the variable T, where:
|
<float1> |
Multiplier on mass matrix term ( d ⁄dt ). |
<float2> |
Multiplier on advective term. |
<float3> |
Multiplier on boundary term ( \(\underline{n}\) • flux ). |
<float4> |
Multiplier on diffusion term. |
<float5> |
Multiplier on source term. |
Note: These multipliers are intended to provide a means of activating or deactivating terms of an equation, and hence should be set to zero or one. If a multiplier is zero, the section of code that evaluates the corresponding term will be skipped.
Examples¶
The following is a sample card that uses a linear continuous interpolation and weight function and has all the term multipliers on:
porous_energy Q1 P_TEMP Q1 1. 1. 1. 1. 1.
Technical Discussion¶
Usage of this equation is discussed extensively in GT-009.3 Output variables in the ExodusII database are POR_TEMP
References¶
GT-009
surf_charge¶
EQ =surf_charge {Galerkin_wt} QS {Interpol_fnc} <float1> <float2> <float3>
<float4> <float5>
Description / Usage¶
This card provides information for solving a conservation equation for the total surface charge in a 2-dimensional bar (or shell) element.. Note that this equation is not yet available in three dimensions and is in fact untested at this time. The card entries are as follows:
surf_charge |
Name of the equation to be solved. |
{Galerkin_wt} |
Two- or four-character value that defines the type of weighting function for this equation, where:
|
QS |
Name of the variable associated with the shell curvature equation. |
{Interpol_fnc} |
Two- or four-character value that defines the interpolation function used to represent the variable QS where:
|
<float1> |
Multiplier for mass terms. Set to 1.0. |
<float2> |
Multiple for advection terms. Set to 1.0. |
<float3> |
Multiplier for boundary terms. Set to 1.0. |
<float4> |
Multiplier for diffusion terms - required but not currently implemented. |
<float5> |
Multiplier for source terms - required but not currently implemented. |
Examples¶
The following is a sample card that uses bilinear surface charge interpolation and weight function:
EQ = surf_charge Q2 QS Q2 1.0 1.0 1.0 0.0 0.0
Technical Discussion¶
The surface charge conservation equation implemented is:
where \(\sigma\) is the surface charge unknown, \(D_s\) is the surface diffusion coefficient, e is the electrical permittivity, \(\underline{n}\) is the unit normal vector to the surface, and \(\underline{E}\) = –\(\Delta\) V is the electric field vector. Here, advection contributions are not considered.
This is a special type of shell equation which depends on the gradient of a bulk variable (here, electric potential V). Since values of these variables away from the surface are normally not accessible during assembly of shell equations, this term has to be applied as a special type of boundary condition (WEAK_SHELL_GRAD) which is set up to evaluate sensitivities to interior bulk variable degrees of freedom . This term, though physically an integral part of the surface charge equation, is applied through the SURFACE_ELECTRIC_FIELD_BC boundary condition.
References¶
Notz, Patrick K. Ph.D. thesis. Purdue University, 2000.
shell_tension¶
EQ = shell_tension {Galerkin_wt} {TENS} {Interpol_fnc} <floatlist>
Description / Usage¶
This card provides information for solving an equation for tension using the structural shell capability in Goma. The capability is based on inextensible cylindrical shells. One material property is associated with this equation and that is the bending stiffness. Note that <floatlist> contains one constant and it should always be set to one. The Galerkin weight and the interpolation function must be the same for the code to work properly.
shell_tens |
Name of the equation to be solved. |
{Galerkin_wt} |
Two- or four-character value that defines the type of weighting function for this equation, where:
|
TENS |
Name of the variable associated with the shell tension equation. |
{Interpol_fnc} |
Two- or four-character value that defines the interpolation function used to represent the variable TENS where:
|
<float1> |
Multiplier on whole equation. Set to 1.0. |
Examples¶
The following is a sample card that uses linear continuous tension interpolation and weight function:
EQ = momentum1 Q1 TENS Q1 1.0
Technical Discussion¶
Complete tutorial on the use of this equation exists. See GT-27.1.
Theory¶
The structural shell equation capability in Goma builds on the shell-element capability built by Pat Notz and Ed Wilkes in FY03. Basically we are solving the following equations for the shell tension (this card) and shell curvature (see shell_curvature equation):
References¶
GT-27
shell_curvature¶
EQ = shell_curvature {Galerkin_wt} {K} {Interpol_fnc} <floatlist>
Description / Usage¶
This card provides information for solving a definition equation for total curvature of a two-dimensional shell element. Note that this equation is not yet available in three dimensions. The curvature is required by the inextensible cylindrical shell capability in Goma. See references cited below. Note that <floatlist> contains one constant and it should always be set to one. The Galerkin weight and the interpolation function must be the same for the code to work properly.
shell_curvature |
Name of the equation to be solved. |
{Galerkin_wt} |
Two- or four-character value that defines the type of weighting function for this equation, where:
|
K |
Name of the variable associated with the shell curvature equation. |
{Interpol_fnc} |
Two- or four-character value that defines the interpolation function used to represent the variable K where:
|
<float1> |
Multiplier on whole equation. Set to 1.0. |
Examples¶
The following is a sample card that uses linear continuous curvature interpolation and weight function:
EQ = momentum1 Q1 K Q1 1.0
Technical Discussion¶
Complete tutorial on the use of this equation exists. See GT-27.
Theory¶
The structural shell equation capability in Goma builds on the shell-element capability built by Pat Notz and Ed Wilkes in FY03. Basically we are solving the following equations for the shell tension and shell curvature (this card):
References¶
GT-27
shell_angle¶
EQ =shell_angle{1 | 2} {Galerkin_wt} {SH_ANG1 | SH_ANG2} {Interpol_fnc}
Description / Usage¶
This card provides information for solving a definition equation for the surface orientation angle in a 2-dimensional bar element. It applies only to shell element blocks. Note that this equation is available in three-dimensional problems but is in fact untested at this time.. The shell angle equation(s) determine the components of the normal vector to the shell surface; since its magnitude is 1 by definition, one less degree of freedom is required tha the number of coordinates. The Galerkin weight and the interpolation function must be the same for the code to work properly.
shell_angle{1|2} |
Name of the equation to be solved. |
{Galerkin_wt} |
Two- or four-character value that defines the type of weighting function for this equation, where:
|
SH_ANG{1|2} |
SH_ANG{1|2} Name of the variable associated with the shell angle equation. |
{Interpol_fnc} |
Two- or four-character value that defines the interpolation function used to represent the variable SH_ANG where:
|
This equation requires no equation term multiplier entries.
Examples¶
The following are sample cards that use linear continuous curvature interpolation and weight function:
EQ = shell_angle1 Q1 SH_ANG1 Q1
EQ = shell_angle2 Q1 SH_ANG2 Q2
The second card applies only to 3D problems.
Technical Discussion¶
For 2D problems, the defining equation is: \(\Theta\) = atan[ \(n_x\), \(n_y\)] where Q is shell_angle1 and \(n_x\) and \(n_y\) are the components of the normal vector to the shell surface. There is an analogous definition for shell_angle2.
References¶
No References.
shell_diff_flux¶
EQ =shell_diff_flux {Galerkin_wt} SH_J {Interpol_fnc} <float1>
Description / Usage¶
This card provides information for solving a conservation equation for the total surface diffusive flux in a 2-dimensional bar (or shell) element. Note that this equation is not yet available in three dimensions and is in fact untested at this time. The card entries are as follows:
shell_diff_flux |
Name of the equation to be solved. |
{Galerkin_wt} |
Two- or four-character value that defines the type of weighting function for this equation, where:
|
SH_J |
Name of the variable associated with the shell curvature equation. |
{Interpol_fnc} |
Two- or four-character value that defines the interpolation function used to represent the variable SH_J where:
|
<float1> |
Multiplier for diffusion terms (in this case, the whole equation). |
Examples¶
The following is a sample card that uses bilinear shell diffusive flux interpolation and weight function:
EQ = shell_diff_flux Q2 SH_J Q2 1.0
Technical Discussion¶
This is only a preliminary implementation of a shell quantity conservation equation. It is not currently operational. When it is fully implemented, the number of required equation term multiplier entries will be adjusted acordingly.
References¶
No References.
shell_diff_curv¶
EQ =shell_diff_curv {Galerkin_wt} SH_KD {Interpol_fnc} <float1>
Description / Usage¶
This card provides information for solving a definition equation for the total surface curvature in a 2-dimensional bar element, intended for use with shell diffusive flux problems. Note that this equation is not yet available in three dimensions and is in fact untested at this time. Note that <floatlist> contains one constant and it should always be set to one. The Galerkin weight and the interpolation function must be the same for the code to work properly.
shell_diff_curv |
Name of the equation to be solved. |
{Galerkin_wt} |
Two- or four-character value that defines the type of weighting function for this equation, where:
|
SH_KD |
Name of the variable associated with the shell curvature equation. |
{Interpol_fnc} |
Two- or four-character value that defines the interpolation function used to represent the variable SH_KD where:
|
<float1> |
Multiplier on diffusion term (i.e. the whole equation). Set to 1.0. |
Examples¶
The following is a sample card that uses linear continuous curvature interpolation and weight function:
EQ = shell_diff_curv Q1 SH_KD Q1 1.0
Technical Discussion¶
The equation solved is the surface curvature definition \(\kappa\) = \(\Delta_s\) \(\underline{n}\) = (I – \(\underline{n}\) \(\underline{n}\)) • \(\Delta\) n. See discussion for EQ = shell_surf_div_v.
References¶
Edwards, D. A., Brenner, H., Wasan, D. T., 1991. Interfacial Transport Processes and Rheology. Butterworth-Heinemann, Boston.
shell_normal¶
EQ =shell_normal{1|2} {Galerkin_wt} {SH_N1|SH_N2} {Interpol_fnc} <float1>
Description / Usage¶
This card specifies a vector of shell normal vector component unknowns in a 2- dimensional bar element, intended for use with shell diffusive flux problems. Note that this equation is not yet available in three dimensions and is in fact untested at this time. Note that <floatlist> contains one constant and it should always be set to one. The Galerkin weight and the interpolation function must be the same for the code to work properly.
shell_normal1 | shell_normal2 |
Name of the equation to be solved. |
{Galerkin_wt} |
Two- or four-character value that defines the type of weighting function for this equation, where:
|
SH_N1 | SH_N2 |
Name of the variable associated with the shell curvature equation. |
{Interpol_fnc} |
Two- or four-character value that defines the interpolation function used to represent the variable SH_N1(2) where:
|
<float1> |
Multiplier on diffusion term (i.e. the whole equation). Set to 1.0. |
Examples¶
The following is a pair of sample cards that use linear continuous normal interpolation and weight function:
EQ = shell_normal1 Q1 SH_N1 Q1 1.0
EQ = shell_normal2 Q1 SH_N2 Q1 1.0
Note that since this equation applies only to 2D problem domains at this time, two cards are needed as shown above (one for each component).
Technical Discussion¶
This equation merely sets the components of the shell normal vector equal to those in fv->snormal, which are calculated rigorously in surface_determinant_and_normal(). Consideration is being given to replacing these with a single unknown for shell normal angle, which contains the same information in a single scalar unknown.
References¶
No References.
shell_surf_curv¶
EQ =shell_surf_curv {Galerkin_wt} gamma2 {Interpol_fnc} <float1>
Description / Usage¶
This card provides information for solving a definition equation for the total surface curvature in a 2-dimensional bar element. Note that this equation is not yet available in three dimensions and is in fact untested at this time. These building blocks are required by the non-Newtonian surface rheology capability in Goma. Note that <floatlist> contains one constant and it should always be set to one. The Galerkin weight and the interpolation function must be the same for the code to work properly.
shell_surf_curv |
Name of the equation to be solved. |
{Galerkin_wt} |
Two- or four-character value that defines the type of weighting function for this equation, where:
|
gamma2 |
Name of the variable associated with the shell curvature equation. |
{Interpol_fnc} |
{Interpol_fnc} Two- or four-character value that defines the interpolation function used to represent the variable K where:
|
<float1> |
Multiplier on whole equation. Set to 1.0. |
Examples¶
The following is a sample card that uses linear continuous curvature interpolation and weight function:
EQ = shell_surf_curv Q1 gamma2 Q1 1.0
Technical Discussion¶
See discussion for EQ = shell_surf_div_v
References¶
Edwards, D. A., Brenner, H., Wasan, D. T., 1991. Interfacial Transport Processes and Rheology. Butterworth-Heinemann, Boston.
shell_surf_div_v¶
EQ = shell_surf_div_v {Galerkin_wt} gamma1 {Interpol_fnc} <float1>
Description / Usage¶
This card provides information for solving a definition equation for surface divergence of the fluid velocity field on a 2-dimensional bar element. Note that this equation is not yet available in three dimensions. This term is required by the non-Newtonian surface rheology capability in Goma. Note that <floatlist> contains one constant and it should always be set to one. The Galerkin weight and the interpolation function must be the same for the code to work properly. Also note that this term is not currently active in Goma, and the developers should be consulted.
shell_surf_div_v |
Name of the equation to be solved. |
{Galerkin_wt} |
Two- or four-character value that defines the type of weighting function for this equation, where:
|
gamma1 |
Name of the variable associated with the shell curvature equation. |
{Interpol_fnc} |
Two- or four-character value that defines the interpolation function used to represent the variable K where:
|
<float1> |
Multiplier on whole equation. Set to 1.0. |
Examples¶
The following is a sample card that uses linear continuous curvature interpolation and weight function:
EQ = shell_surf_div_v Q1 gamma1 Q1 1.0
Technical Discussion¶
This shell equation is required for proper computation of the Boussinesq-Scriven surface rheological constitutive equation (namely the surface divergence of the velocity field in the 4th and 6th terms on the right of the following equation). The functional form of this equation is as follows:
Here, \(\Delta_s\) \(\equiv\) (\(\underline{I}\) – \(\underline{n}\) \(\underline{n}\)) ⋅ \(\Delta\) is the surface gradient operator, and \(I_s\) \(\equiv\) (\(\underline{I}\) – \(\underline{n}\) \(\underline{n}\)) is the surface unit tensor. \(\mu_s\) and \(\kappa_s\) are the surface shear viscosity and surface extensional viscosity, respectively. Note that the first three terms on the right are balance of the stress in the standard Goma CAPILLARY condition, with surface tension gradients being accommodated through variable surface tension. The boundary condition CAPILLARY_SHEAR_VISC is used to set the additional terms of this constitutive equation. As of January 2006 only the 7th term on the right hand side is implemented, as it is the only nonzero term in a flat surface shear viscometer. The building blocks for the other terms are available through additional shell equations. These remaining terms actually represent additional dissipation caused by surface active species microstructures flowing in the surface. The best source of discussion of this equation is a book by Edwards et al. (1991. Interfacial Transport Processes and Rheology. Butterworth-Heinemann, Boston).
References¶
Edwards, D. A., Brenner, H., Wasan, D. T., 1991. Interfacial Transport Processes and Rheology. Butterworth-Heinemann, Boston.
grad_v_dot_n1, grad_v_dot_n2, grad_v_dot_n3¶
EQ = grad_v_dot_n[1|2|3] {Galerkin_wt} gamma3_[1|2|3] {Interpol_fnc} <float1>
Description / Usage¶
This card provides information for solving a definition equation for the normal components of the velocity gradient tensor in a 2-dimensional bar element. Note that this equation is not yet available in three dimensions and is in fact untested at this time.. These building blocks are required by the non-Newtonian surface rheology capability in Goma. Note that <floatlist> contains one constant and it should always be set to one. The Galerkin weight and the interpolation function must be the same for the code to work properly.
grad_v_dot_n1, grad_v_dot_n2, grad_v_dot_n3 |
Name of the equation to be solved. |
{Galerkin_wt} |
Two- or four-character value that defines the type of weighting function for this equation, where:
|
gamma3_[1|2|3] |
Name of the variable associated with the shell curvature equation. |
{Interpol_fnc} |
Two- or four-character value that defines the interpolation function used to represent the variable K where:
|
<float1> |
Multiplier on whole equation. Set to 1.0. |
Examples¶
The following is a sample card that uses linear continuous curvature interpolation and weight function:
EQ = grad_v_dot_n1 Q1 gamma3_1 Q1 1.0
Technical Discussion¶
See discussion for EQ=shell_surf_div_v
References¶
Edwards, D. A., Brenner, H., Wasan, D. T., 1991. Interfacial Transport Processes and Rheology. Butterworth-Heinemann, Boston.
n_dot_curl_v¶
EQ = n_dot_curl_v {Galerkin_wt} gamma4 {Interpol_fnc} <float1>
Description / Usage¶
This card provides information for solving a definition equation for the normal component of the surface curl of the velocity field on a 2-dimensional bar element. Note that this equation is not yet available in three dimensions. This term is required by the non-Newtonian surface rheology capability in Goma. Note that <floatlist> contains one constant and it should always be set to one. The Galerkin weight and the interpolation function must be the same for the code to work properly.
n_dot_curl_v |
Name of the equation to be solved. |
{Galerkin_wt} |
Two- or four-character value that defines the type of weighting function for this equation, where:
|
gamma4 |
Name of the variable associated with the shell curvature equation. |
{Interpol_fnc} |
{Interpol_fnc} Two- or four-character value that defines the interpolation function used to represent the variable K where:
|
<float1> |
Multiplier on whole equation. Set to 1.0. |
Examples¶
The following is a sample card that uses linear continuous curvature interpolation and weight function:
EQ = n_dot_curl_v Q1 gamma4 Q1 1.0
Technical Discussion¶
This shell equation is required for proper computation of the Boussinesq-Scriven surface rheological constitutive equation elements (namely the surface curl of the velocity field, normal component) in the 7th term on the right of the following equation):
Here, \(\Delta_s\) \(\equiv\) (\(\underline{I}\) – \(\underline{n}\) \(\underline{n}\)) ⋅ \(\Delta\) is the surface gradient operator, and \(I_s\) \(\equiv\) (\(\underline{I}\) – \(\underline{n}\) \(\underline{n}\)) is the surface unit tensor. \(\mu_s\) and \(\kappa_s\) are the surface shear viscosity and surface extensional viscosity, respectively. Note that the first three terms on the right are balance of the stress in the standard Goma CAPILLARY condition, with surface tension gradients being accommodated through variable surface tension. The boundary condition CAPILLARY_SHEAR_VISC is used to set the additional terms of this constitutive equation. As of January 2006 only the 7th term on the right hand side is implemented, as it is the only nonzero term in a flat surface shear viscometer. The building blocks for the other terms are available through additional shell equations. These remaining terms actually represent additional dissipation caused by surface active species microstructures flowing in the surface. The best source of discussion of this equation is a book by Edwards et al. (1991. Interfacial Transport Processes and Rheology. Butterworth-Heinemann, Boston).
References¶
Edwards, D. A., Brenner, H., Wasan, D. T., 1991. Interfacial Transport Processes and Rheology. Butterworth-Heinemann, Boston.
acous_preal¶
EQ = acous_preal {Galerkin_wt} APR {Interpol_fnc} <float list>
Description / Usage¶
This card provides information for solving a differential equation for the real part of the harmonic acoustic wave equation. Definitions of the input parameters are defined below. Note that <float1> through <float5> define the constant multipliers in front of each type of term in the equation. The Galerkin weight and the interpolation function must be the same for the code to work properly.
acous_preal |
Name of the equation to be solved. |
{Galerkin_wt} |
Two-character value that defines the type of weighting function for this equation, where:
|
APR |
Name of the variable associated with this equation. |
{Interpol_fnc} |
Two-character value that defines the interpolation
|
<float1> |
currently not used. |
<float2> |
Multiplier on acoustic absorption term. |
<float3> |
Multiplier on boundary terms. |
<float4> |
Multiplier on Laplacian term. |
<float5> |
Multiplier on pressure term. |
Note: These multipliers are intended to provide a means of activating or deactivating terms of an equation, and hence should be set to zero or one. If a multiplier is zero, the section of code that evaluates the corresponding term will be skipped.
Examples¶
The following is a sample card that uses quadratic continuous interpolation for the species equation and turns on all the term multipliers:
EQ = acous_preal Q2 APR Q2 0. 1. 1. 1. 1.
Technical Discussion¶
Harmonic form of the wave equation with absorption (attenuation) included. P is the amplitude of the acoustic pressure (complex), k is the wavenumber, \(\alpha\) is the absorption coefficient, and \(\omega\) is the frequency (rad/sec).
acous_pimag¶
EQ = acous_pimag {Galerkin_wt} API {Interpol_fnc} <float list>
Description / Usage¶
This card provides information for solving a differential equation for the imaginary part of the harmonic acoustic wave equation. Definitions of the input parameters are defined below. Note that <float1> through <float5> define the constant multipliers in front of each type of term in the equation. The Galerkin weight and the interpolation function must be the same for the code to work properly.
acous_pimag |
Name of the equation to be solved. |
{Galerkin_wt} |
Two-character value that defines the type of weighting function for this equation, where:
|
API |
Name of the variable associated with this equation. |
{Interpol_fnc} |
Two-character value that defines the interpolation function used to represent the variable SH, where:
|
<float1> |
currently not used. |
<float2> |
Multiplier on acoustic absorption term. |
<float3> |
Multiplier on boundary terms. |
<float4> |
Multiplier on Laplacian term. |
<float5> |
Multiplier on pressure term. |
Note: These multipliers are intended to provide a means of activating or deactivating terms of an equation, and hence should be set to zero or one. If a multiplier is zero, the section of code that evaluates the corresponding term will be skipped.
Examples¶
The following is a sample card that uses quadratic continuous interpolation for the species equation and turns on all the term multipliers:
EQ = acous_pimag Q2 API Q2 0. 1. 1. 1. 1.
Technical Discussion¶
Harmonic form of the wave equation with absorption (attenuation) included. P is the amplitude of the acoustic pressure (complex), k is the wavenumber, \(\alpha\) is the absorption coefficient, and \(\omega\) is the frequency (rad/sec).
acous_reyn_stress¶
EQ = acous_reyn_stress {Galerkin_wt} ARS {Interpol_fnc} <float list>
Description / Usage¶
This card provides information for solving a differential equation for the Reynolds stress that results from time averaging of the acoustic pressure and velocity fields. Interactions of the fluid momentum equations with the acoustic wave equations are then afforded through gradients of the scalar acoustic Reynolds stress with the use of the ACOUSTIC Navier-Stokes source. Definitions of the input parameters are defined below. Note that <float1> through <float3> define the constant multipliers in front of each type of term in the equation. The Galerkin weight and the interpolation function must be the same for the code to work properly.
acous_reyn_stress |
Name of the equation to be solved. |
{Galerkin_wt} |
Two-character value that defines the type of weighting function for this equation, where:
|
ARS |
Name of the variable associated with this equation. |
{Interpol_fnc} |
Two-character value that defines the interpolation function used to represent the variable SH, where:
|
<float1> |
Multiplier for the Reynolds stress variable. |
<float2> |
Multiplier for the kinetic energy term. |
<float3> |
Multiplier for the compressional energy term. |
Note: These multipliers are intended to provide a means of activating or deactivating terms of an equation, and hence should be set to zero or one. If a multiplier is zero, the section of code that evaluates the corresponding term will be skipped.
Examples¶
The following is a sample card that uses quadratic continuous interpolation for the acoustic Reynolds stress equation and turns on all the term multipliers:
EQ = acous_reyn_stress Q2 ARS Q2 . 1. 1. 1.
Technical Discussion¶
The Reynolds stress due to acoustic fields reduces to a combination of compressional and kinetic energy terms which can be expressed in terms of the magnitude of the acoustic pressure and its gradient. P is the amplitude of the acoustic pressure (complex), k is the wavenumber, R is the acoustic impedance, and \(\omega\) is the frequency (rad/sec).
potential1¶
EQ = potential1 {Galerkin_wt} PHI1 {Interpol_fnc} <floatlist>
Description / Usage¶
This card provides information for solving a differential equation for the solid-phase electrode potential. This electrode-potential equation is solved together with the liquidphase electrolyte-potential equation (see the potential2 card) for simulating electrochemical processes (such as thermal batteries and proton-exchange-membrane fuel cells) involving simultaneous charge transport in both the liquid-electrolyte and solid-electrode phases (as in the porous anode and cathode). Definitions of the input parameters are defined below. Note that <floatlist> has five parameters to define the constant multipliers in front of each type of term in the equation. The Galerkin weight and the interpolation function must be the same for the code to work properly.
potential1 |
Name of the equation to be solved. |
{Galerkin_wt} |
Two-character value that defines the type of weighting function for this equation, where:
|
PHI1 |
Name of the variable associated with this equation. |
{Interpol_fnc} |
{Interpol_fnc} Two-character value that defines the interpolation function used to represent the variable PHI1, where:
|
<float1> |
Multiplier on mass matrix term ( d ⁄dt ). |
<float2> |
Multiplier on advective term. |
<float3> |
Multiplier on boundary term ( \(\underline{n}\) • flux ). |
<float4> |
Multiplier on diffusion term. |
<float5> |
Multiplier on source term. |
Note: These multipliers are intended to provide a means of activating or deactivating terms of an equation, and hence should be set to zero or one. If a multiplier is zero, the section of code that evaluates the corresponding term will be skipped.
Examples¶
The following is a sample card that uses a quadratic interpolation and weight function and turns off the mass (or transient) and advection terms but turns on the boundary, diffusion, and source terms:
EQ = potential1 Q2 PHI1 Q2 0. 0. 1. 1. 1.
Technical Discussion¶
No Discussion.
References¶
No References.
potential2¶
EQ = potential2 {Galerkin_wt} PHI2 {Interpol_fnc} <floatlist>
Description / Usage¶
This card provides information for solving a differential equation for the liquid-phase electrolyte potential. This electrolyte-potential equation is solved together with the solid-phase electrode-potential equation (see the potential1 card) for simulating electrochemical processes (such as thermal batteries and proton-exchange-membrane fuel cells) involving simultaneous charge transport in both the liquid-electrolyte and solid-electrode phases (as in the porous anode and cathode). Definitions of the input parameters are defined below. Note that <floatlist> has five parameters to define the constant multipliers in front of each type of term in the equation. The Galerkin weight and the interpolation function must be the same for the code to work properly.
potential2 |
Name of the equation to be solved. |
{Galerkin_wt} |
Two-character value that defines the type of weighting function for this equation, where:
|
PHI2 |
Name of the variable associated with this equation. |
{Interpol_fnc} |
Two-character value that defines the interpolation function used to represent the variable PHI2, where:
|
<float1> |
Multiplier on mass matrix term ( d ⁄dt ). |
<float2> |
Multiplier on advective term. |
<float3> |
Multiplier on boundary term ( \(\underline{n}\) • flux ). |
<float4> |
Multiplier on diffusion term. |
<float5> |
Multiplier on source term. |
Note: These multipliers are intended to provide a means of activating or deactivating terms of an equation, and hence should be set to zero or one. If a multiplier is zero, the section of code that evaluates the corresponding term will be skipped.
Examples¶
The following is a sample card that uses a quadratic interpolation and weight function and turns off the mass (or transient) and advection terms but turns on the boundary, diffusion, and source terms:
EQ = potential2 Q2 PHI2 Q2 0. 0. 1. 1. 1.
Technical Discussion¶
No Discussion.
References¶
No References.
lubp¶
EQ = lubp {Galerkin_wt} LUBP {Interpol_fnc} <floatlist>
Description / Usage¶
This card provides information for solving the Reynold’s lubrication equation for confined flow. Definitions of the input parameters are defined below. The Galerkin weight and the interpolation function must be set the same for the code to work properly. Counterparts to this equation for lubrication flow of capillary films (filmequations) are shell_filmp and shell_filmh equations.
lubp |
Name of equation to be solved. |
{Galerkin_wt} |
Two-or four-character value that defines the type of weighting function for this equation, where:
|
LUBP |
Name of the variable associated with this equation. |
{Interpol_fnc} |
Two-or four-character value that defines the interpolation function for the variable LUBP, where:
|
<float1> |
Multiplier for the mass matrix term (not used yet as of 3/4/2010). |
<float2> |
Multiplier for the diffusion term. |
<float3> |
Multiplier for the source term. |
Examples¶
Following is a sample card:
EQ = lubp Q1 LUBP Q1 1. 1. 1.
This applies the confined flow lubrication equation with all terms activated.
Technical Discussion¶
The equation solved is as follows:
The first term multiplier, activating the mass (time-derivative) term is not currently activated as the gap-height is user-prescribed.
The second term multiplier affects the third and fourth terms (grad_p and surface tension terms).
The third term multiplier activates the Couette flow terms.
lubp_2¶
EQ = lubp_2 {Galerkin_wt} LUBP {Interpol_fnc} <floatlist>
Description / Usage¶
This card provides information for solving a second-layer Reynold’s lubrication equation for confined flow. The second layer is solved on an adjacent shell as lubp equation but shares the same nodes. Please consult tutorials for proper usuage. This equation can be used to model transport between alternating stacks of porous materials. Definitions of the input parameters are defined below. The Galerkin weight and the interpolation function must be set the same for the code to work properly. Counterparts to this equation for lubrication flow of capillary films (film-equations) are shell_filmp and shell_filmh equations.
lubp_2 |
Name of equation to be solved. |
{Galerkin_wt} |
Two-or four-character value that defines the type of weighting function for this equation, where:
|
LUBP_2 |
Name of the variable associated with this equation. |
{Interpol_fnc} |
Two-or four-character value that defines the interpolation function for the variable LUBP_2 where:
|
<float1> |
Multiplier for the mass matrix term (not used yet as of 3/4/2010). |
<float2> |
Multiplier for the diffusion term. |
<float3> |
Multiplier for the source term. |
Examples¶
Following is a sample card:
EQ = lubp_2 Q1 LUBP_2 Q1 1. 1. 1.
This applies the confined flow lubrication equation with all terms activated.
Technical Discussion¶
The equation solved is as follows:
The first term multiplier, activating the mass (time-derivative) term is not currently activated as the gap-height is user-prescribed.
The second term multiplier affects the third and fourth terms (grad_p and surface tension terms).
The third term multiplier activates the Couette flow terms.
shell_energy¶
EQ = shell_energy {Galerkin_wt} SH_T {Interpol_fnc} <floatlist>
Description / Usage¶
This card provides information for solving a shell thermal energy equation. Use of this equation can be made for any shell, including those which involve Reynold’s film or confined flow lubrication flow. Definitions of the input parameters are defined below. The Galerkin weight and the interpolation function must be set the same for the code to work properly.
shell_energy |
Name of equation to be solved. |
{Galerkin_wt} |
Two-or four-character value that defines the type of weighting function for this equation, where:
|
SH_T |
Name of the variable associated with this equation. |
{Interpol_fnc} |
Two-or four-character value that defines the interpolation function for the variable SH_T, where:
|
<float1> |
Multiplier for the mass matrix term. |
<float2> |
Multiplier for the advection term. |
<float3> |
Multiplier for the boundary term (not used). |
<float4> |
Multiplier for the source term. |
Examples¶
Following is a sample card:
EQ = shell_energy Q1 SH_T Q1 1. 1. 1. 1. 1.
This applies the shell energy equation with all terms activated on a SHELL4 or BAR2 mesh.
Technical Discussion¶
The equation solved is as follows:
Clearly this equation looks similar to the standard energy equation for continuum formulations, but the presence of the gap/film thickness h indications that the assumption of a constant shell temperature across the thickness is assumed, and hence all the terms are constant in that integrated direction. The source terms are all invoked in the material files, and there are many types and many submodels.
Special NOTE: This equation can be up-winded for high Peclet number flows. If the Energy Weight Function card in the companion material file is set to SUPG, then the advection term is stabilized with standard streamwise-upwinding-Petrov- Galerkin approach.
shell_filmp¶
EQ = shell_filmp {Galerkin_wt} SHELL_FILMP {Interpol_fnc} <floatlist>
Description / Usage¶
This card provides information for solving the film lubrication equation for free surface flow. Definitions of the input parameters are defined below. The Galerkin weight and the interpolation function must be set the same for the code to work properly. Counterparts to this equation for lubrication flow of capillary films (film-equations) are lup_p equation.
shell_filmp |
Name of equation to be solved. |
{Galerkin_wt} |
Two-or four-character value that defines the type of weighting function for this equation, where:
|
SHELL_FILMP |
Name of the variable associated with this equation. |
{Interpol_fnc} |
Two-or four-character value that defines the interpolation function for the variable SHELL_FILMP, where:
|
<float1> |
Multiplier for the mass matrix term. |
<float2> |
Multiplier for the advection term. It is not activated. |
<float3> |
Multiplier for the boundary term. It is not activated. |
<float4> |
Multiplier for the diffusion term. |
<float5> |
Multiplier for the source term. |
Examples¶
Following is a sample card:
EQ = shell_filmp Q1 SHELL_FILMP Q1 1. 0. 0. 1. 1.
This applies the film flow equation with all terms activated.
Technical Discussion¶
The equation solved is as follows:
The mass matrix multiplier activates the time-derivative term.
The diffusion multiplier activates the terms inside the divergence operator and represents the flux or the flow rate of the liquid film.
The source (or sink, in this case,) activates the last term, rate of evaporation.
This equation has to be used with the equation describing SHELL_FILMH.
shell_filmh¶
EQ = shell_filmh {Galerkin_wt} SHELL_FILMH {Interpol_fnc} <floatlist>
Description / Usage¶
This card provides information for solving the film lubrication equation for free surface flow. Definitions of the input parameters are defined below. The Galerkin weight and the interpolation function must be set the same for the code to work properly.
Counterparts to this equation for lubrication flow of capillary films (film-equations) are lup_p equation.
shell_filmh |
Name of equation to be solved. |
{Galerkin_wt} |
Two-or four-character value that defines the type of weighting function for this equation, where:
|
SHELL_FILMH |
Name of the variable associated with this equation. |
{Interpol_fnc} |
Two-or four-character value that defines the interpolation function for the variable SHELL_FILMH, where:
|
<float1> |
Multiplier for the mass matrix term. It is not activated. |
<float2> |
Multiplier for the advection term. It is not activated. |
<float3> |
Multiplier for the boundary term. It is not activated. |
<float4> |
Multiplier for the diffusion term. |
<float5> |
Multiplier for the source term. |
Examples¶
Following is a sample card:
EQ = shell_filmh Q1 SHELL_FILMH Q1 0. 0. 0. 1. 1.
This applies the film flow equation with all terms activated.
Technical Discussion¶
The equation solved is as follows:
The diffusion multiplier activates the capillary pressure term.
The source activates the first term.
This equation does not fit the general prototype of conservation equation where the diffusion and source terms really apply. In all cases, both diffusion and source terms need to be activated.
This equation has to be used with the equation describing SHELL_FILMP.
shell_partc¶
EQ = shell_partc {Galerkin_wt} SHELL_PARTC {Interpol_fnc} <floatlist>
Description / Usage¶
This card provides information for solving the z-averaged concentration of particles inside film flow. Definitions of the input parameters are defined below. The Galerkin weight and the interpolation function must be set the same for the code to work properly.
shell_partc |
Name of equation to be solved. |
{Galerkin_wt} |
Two-or four-character value that defines the type of weighting function for this equation, where:
|
SHELL_PARTC |
Name of the variable associated with this equation. |
{Interpol_fnc} |
Two-or four-character value that defines the interpolation function for the variable SHELL_PARTC, where:
|
<float1> |
Multiplier for the mass matrix term. |
<float2> |
Multiplier for the advection term. |
<float3> |
Multiplier for the boundary term. It is not activated. |
<float4> |
Multiplier for the diffusion term. |
<float5> |
Multiplier for the source term. |
Examples¶
Following is a sample card:
EQ = shell_partc Q1 SHELL_PARTC Q1 1. 0. 0. 1. 0.
This applies the film flow equation with all terms activated.
Technical Discussion¶
The equation solved is as follows:
The mass matrix multiplier activates the time-derivative term.
The advection multiplier activates the second term, where the flow rate is dotted onto the gradient of particles concentration and it represents advection of particles due to the liquid film flow.
The diffusion multiplier activates the terms inside the divergence operator and represents the Fickian diffusion of particles.
The source activates the last term, rate of evaporation of liquid that contributes to the increase of the particles conentration.
This equation has to be used with the film profile equation describing SHELL_FILMP and SHELL_FILMH.
shell_sat_closed¶
EQ = shell_sat_closed {Galerkin_wt} SH_SAT_CLOSED {Interpol_fnc} <floatlist>
Description / Usage¶
This card provides the capability to solve the porous shell equations for closed (noninterconnected) structured pores. The Galerkin weight and the interpolation function must be set the same for the code to work properly. The counterpart to this equation is porous_sat_open, which solves for interconnected pores.
shell_sat_closed |
Name of equation to be solved. |
{Galerkin_wt} |
Two-or four-character value that defines the type of weighting function for this equation, where:
|
SH_SAT_CLOSED |
Name of the variable associated with this equation. |
{Interpol_fnc} |
Two-or four-character value that defines the interpolation function for the variable SH_SAT_CLOSED, where:
|
<float1> |
Multiplier for the mass matrix term. |
<float2> |
Multiplier for the source term. |
Examples¶
Following is a sample card:
EQ = shell_sat_closed Q1 SH_SAT_CLOSED Q1 1.0 1.0
This applies the equation with all terms activated.
Technical Discussion¶
The equation solved is as follows:
The mass matrix multiplier activates the time-derivative term.
The source matrix multiplier activates the remaining term.
This equation is required to couple with LUBP to solve for the lubrication forces.
Currently, this equation assumes that the porous shell is located in the +z direction of the lubrication shell, and the coupling is set up to draw liquid from the lubrication layer by adding a sink term into the lubrication equations.
Beyond the standard porous media material cards for continuum element regions, one needs in the thin-shell material inputs in the following section:
Porous Shell Closed Porosity = CONSTANT 0.1
Porous Shell Height = CONSTANT 1.0
Porous Shell Radius = CONSTANT 0.01
Porous Shell Atmospheric Pressure = CONSTANT 1.e6
Porous Shell Reference Pressure = CONSTANT 0.
Porous Shell Cross Permeability = CONSTANT 0.2
Porous Shell Initial Pore Pressure = CONSTANT 0.
Please read the associated material property cards sections for details.
shell_sat_gasn¶
EQ = shell_sat_gasn {Galerkin_wt} SH_SAT_GASN {Interpol_fnc} <floatlist>
Description / Usage¶
This card provides the capability to solve the porous shell equation for the inventory of trapped gas in a closed pore shell simulation, viz. the EQ=shell_sat_closed. The equation tracks the inventory of trapped gas and accounts for the compression (ideal gas law) and dissolution into the invading liquid. Two terms are required in this equation:
shell_sat_gasn |
Name of equation to be solved. |
{Galerkin_wt} |
Two-or four-character value that defines the type of weighting function for this equation, where:
|
SH_SAT_GASN |
Name of the variable associated with this equation. |
{Interpol_fnc} |
Two-or four-character value that defines the interpolation function for the variable SH_SAT_GASN, where:
|
<float1> |
Multiplier for the mass matrix term. |
<float2> |
Multiplier for the source term. |
Examples¶
Following is a sample card:
EQ = shell_sat_gasn Q1 SH_SAT_GASN Q1 1.0 1.0
This applies the equation with all terms activated.
Technical Discussion¶
No Discussion.
References¶
Roberts and P. R. Schunk 2012. In preparation.
shell_sat_open¶
EQ = shell_sat_open {Galerkin_wt} SH_P_OPEN {Interpol_fnc} <floatlist>
Description / Usage¶
This card provides the capability to solve the porous shell equations for open (interconnected) structured pores. The Galerkin weight and the interpolation function must be set the same for the code to work properly. The counterpart to this equation is shell_sat_closed, which solves for non-interconnected pores.
shell_sat_open |
Name of equation to be solved. |
{Galerkin_wt} |
Two-or four-character value that defines the type of weighting function for this equation, where:
|
SH_SAT_OPEN |
Name of the variable associated with this equation. |
{Interpol_fnc} |
Two-or four-character value that defines the interpolation function for the variable SH_P_OPEN, where:
|
<float1> |
Multiplier for the mass matrix term. |
<float2> |
Multiplier for the source term. |
Examples¶
Following is a sample card:
EQ = shell_sat_open Q1 SH_P_OPEN Q1 1.0 1.0
This applies the equation with all terms activated.
Technical Discussion¶
The equation solved is as follows:
The mass matrix multiplier activates the time-derivative term.
The source matrix multiplier activates the remaining term.
This equation is required to couple with LUBP to solve for the lubrication forces.
Currently, this equation assumes that the porous shell is located in the +z direction of the lubrication shell, and the coupling is set up to draw liquid from the lubrication layer by adding a sink term into the lubrication equations.
NOT FULLY IMPLEMENTED.
Note that this equation requires the Media Type to be set to POROUS_SHELL_UNSATURATED. With this media type the porous properties for the most part are extracted from the regular (non-shell) porous media property cards, e.g. Permeability, Porosity, Saturation, etc. There are a few exceptions, however. Beyond the standard porous media material cards for continuum element regions, one needs in the thin-shell material inputs the following section:
Porous Shell Closed Porosity = CONSTANT 0.1
Porous Shell Height = CONSTANT 1.0
Porous Shell Radius = CONSTANT 0.01
Porous Shell Atmospheric Pressure = CONSTANT 1.e6
Porous Shell Reference Pressure = CONSTANT 0.
Porous Shell Cross Permeability = CONSTANT 0.2
Porous Shell Initial Pore Pressure = CONSTANT 0.
Please read the associated material property cards sections for details.
shell_sat_open_2¶
EQ = shell_sat_open_2 {Galerkin_wt} SH_P_OPEN_2 {Interpol_fnc} <floatlist>
Description / Usage¶
This card provides the capability to solve a second porous shell equation for open (interconnected) structured pores. The use of this equation requires that the shell material share the same nodes but be a distinct material from that which shell_sat_open resides. Please see the associated tutorials. The Galerkin weight and the interpolation function must be set the same for the code to work properly. The counterpart to this equation is shell_sat_closed, which solves for non-interconnected pores.
shell_sat_open_2 |
Name of equation to be solved. |
{Galerkin_wt} |
Two-or four-character value that defines the type of weighting function for this equation, where:
|
SH_SAT_OPEN_2 |
Name of the variable associated with this equation. |
{Interpol_fnc} |
Two-or four-character value that defines the interpolation function for the variable SH_P_OPEN_2, where:
|
<float1> |
Multiplier for the mass matrix term. |
<float2> |
Multiplier for the source term. |
Examples¶
Following is a sample card:
EQ = shell_sat_open_2 Q1 SH_P_OPEN_2 Q1 1.0 1.0
This applies the equation with all terms activated.
Technical Discussion¶
The equation solved is as follows:
The mass matrix multiplier activates the time-derivative term.
The source matrix multiplier activates the remaining term.
This equation is required to couple with LUBP to solve for the lubrication forces.
Currently, this equation assumes that the porous shell is located in the +z direction of the lubrication shell, and the coupling is set up to draw liquid from the lubrication layer by adding a sink term into the lubrication equations.
NOT FULLY IMPLEMENTED.
shell_deltah¶
EQ = shell_deltah {Galerkin_wt} SH_DH {Interpol_fnc} <floatlist>
Description / Usage¶
This card provides the capability to solve an evolution equation for a changing lubrication gap. The most common example of this would be a melting slider, as in the substrate of a snow ski or during high-energy sliding contact. Melting would change the lubrication gap. The Galerkin weight and the interpolation function must be set the same for the code to work properly. This equation could be furbished or advanced to handle other moving boundary problems which would lead to a changing gap. It should be noted, that gap changes due to a bounding flexible solid structure are already accommodated and fully compatible with this condition.
shell_deltah |
Name of equation to be solved. |
{Galerkin_wt} |
Two-or four-character value that defines the type of weighting function for this equation, where:
|
SH_DH |
Name of the variable associated with this equation. |
{Interpol_fnc} |
Two-or four-character value that defines the interpolation function for the variable SH_DH, where:
|
<float1> |
Multiplier for the mass matrix term. |
<float2> |
Multiplier for the source term. |
Examples¶
Following is a sample card:
EQ = shell_deltah Q1 SH_DH Q1 1.0 1.0
This applies the equation with all terms activated.
Technical Discussion¶
The equation solved is as follows:
where \(E_0\) is the enthalpy, including the effect of phase change through the latent heat material property specified in the material file. \(H_{trans}\) is a heat transfer coefficient and is set in the material file as that due to melting/sliding contact (see material file section on MELTING_CONTACT). dh is the unknown.
The mass matrix multiplier activates the time-derivative term.
The source matrix multiplier activates the remaining term.
This equation is required to couple with SH_TEMP to solve for the local temperature. f
END OF EQ¶
END OF EQ
Description / Usage¶
This card specifies the end of the list of equations in a material section of the Problem Description File. It is only used when automatic equation counting is used, as described and activated in the Number of EQ card. If the value of <integer> in that card is set to -1, all EQ cards below this card are ignored, and Goma counts the number of EQ cards between the Number of EQ card and the END OF EQ card.
Note that the END of EQ card should appear in every material section for which automatic equation counting is being used.
Technical Discussion¶
No Discussion.
END OF MAT¶
END OF MAT
Description / Usage¶
This card specifies the end of the list of materials. It is only used when automatic material counting is used, as described and activated in the Number of Materials card. If the value of <integer> in the Number of Materials card is set to -1, all MAT cards below the END OF MAT card are ignored, and Goma counts the number of MAT cards between these two cards.
Technical Discussion¶
No Discussion.