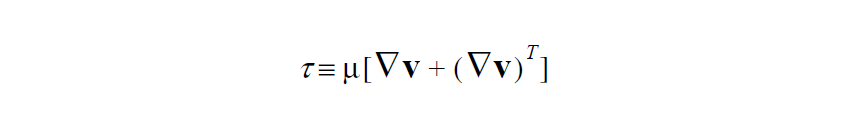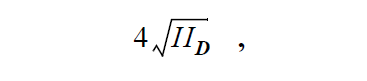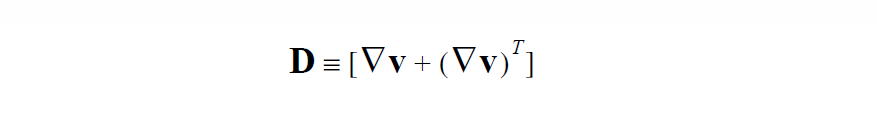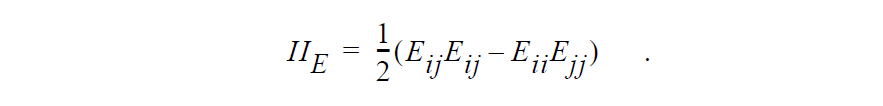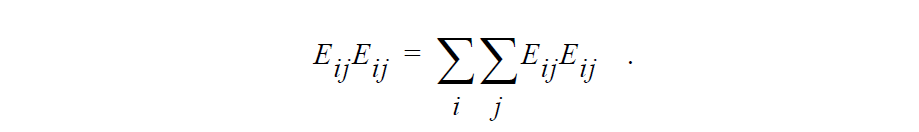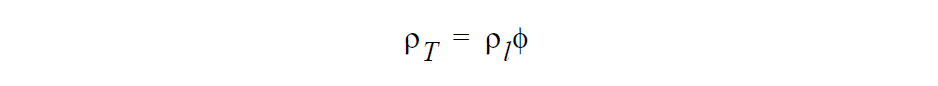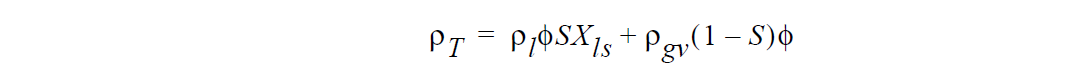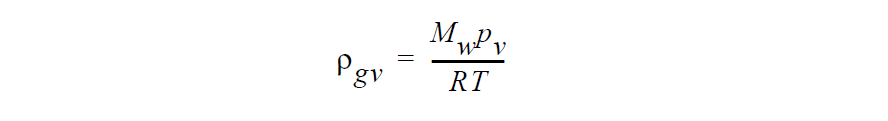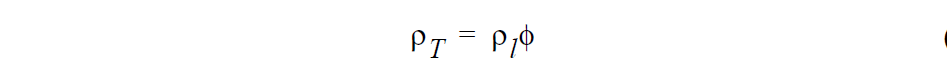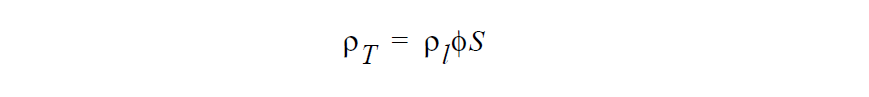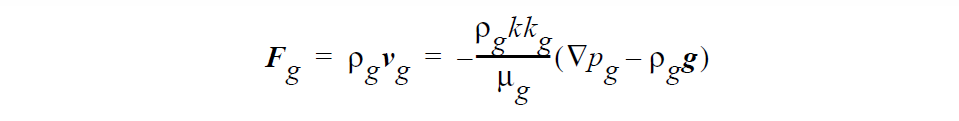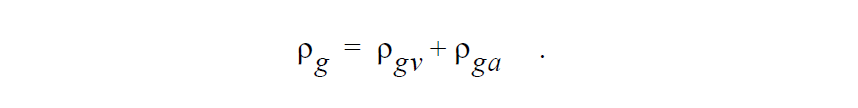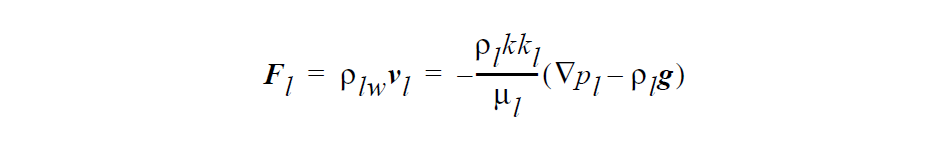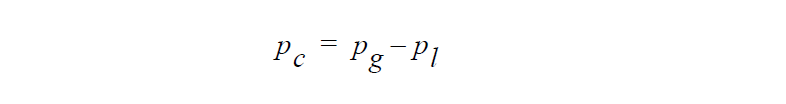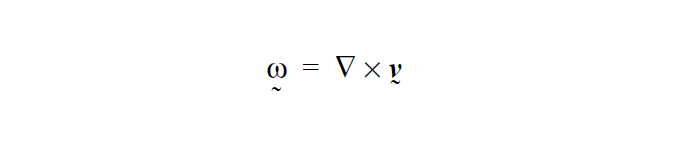Post Processing Specifications¶
This section lists the post-processing options that are accessible within Goma. Each card below triggers calculations of the nodal values of a given function, which are then written to the EXODUS II output file. Normally these values are smoothed before writing them to the output file. For most of these cards a keyword is the only input; if the keyword is yes, the post-processing variable is calculated and written to the file; if the keyword is no, no output is generated for that variable. All of these cards are optional and can appear in any order.
The sections below list the post-processing options and a brief description of each. Users are cautioned - for large, time-dependent runs, the output of many post-processing variables may lead to excessively large EXODUS II output files.
Stream Function¶
Stream Function = {yes | no}
Description / Usage¶
The stream function provides a visual representation of the flow field in incompressible fluids and is derived from the fluid velocity components identified in the Output Exodus II file card.
This auxiliary field triggered by “yes” on this card results in a nodal variable that is called STREAM in the output EXODUS II file.
The permissible values for this postprocessing option are:
yes |
Calculate the stream function. |
no |
Do not calculate the stream function. |
Technical Discussion¶
This function is computed with an element-by-element volumetric flow calculation routine. Poor element quality can result in “kinks” in the stream function field when contoured.
It is important to construct a mesh whose elements are contiguously ordered in such a way that there are no isolated clusters as the elements are swept, i.e., element n+1 must be in contact with one of the previous n elements. NOTE: as of 4/2001 an automatic element reordering scheme based on Reverse Cuthill-McKee algorithm has been implemented in Goma. Automatic ordering can be assured by issuing the OPtimize command to the FASTQ meshing module (cf. Blacker 1988). Most other mesh generators do not provide this service, viz. they do not put out an element order-map field in the EXODUS II file.
NOTE: THIS FUNCTION IS NOT AVAILABLE IN THREE DIMENSIONS, but pathlines, which are equivalent to streamlines for steady flows can be computed in many graphics packages, like Mustafa (Glass, 1995).
References¶
SAND88-1326: FASTQ Users Manual: Version 1.2, Sandia Technical Report, Blacker, T. D. 1988.
Mustafa, Glass, M. W., Personal Communication, 1995
Streamwise Normal Stress¶
Streamwise normal stress = {yes | no}
Description / Usage¶
The stream-wise normal stress, \(T_{tt}\), is defined as tt: \(\tau\), where t is the unit tangent vector to the streamlines computed as v ⁄ \(\mid\) v \(\mid\) and \(\tau\) is the deviatoric part of the dissipative stress tensor,
associated with the Navier-Stokes equations. This variable is called SNS in the output EXODUS II file.
The permissible values for this postprocessing option are
yes |
Calculate the stream-wise normal stress. |
no |
Do not calculate the stream-wise normal stress. |
Technical Discussion¶
As of 2/9/02 this function is computed with the based viscosity, and not the strain-rate dependent viscosity as might be the case for viscosity models other than NEWTONIAN (see Viscosity card).
Cross-Stream Shear Rate¶
Cross-stream shear rate = {yes | no}
Description / Usage¶
As of 2/9/02, it is recommended that this card not be used.
The quantity as computed in Goma is only applicable in two-dimensions and it is not clear what this quantity is, as it is computed. (PRS)
Examples¶
No Examples.
Technical Discussion¶
No Discussion.
References¶
No References.
Mean Shear Rate¶
Mean shear rate = {yes | no}
Description / Usage¶
The mean shear rate is defined as
where \(II_D\) is the second invariant of D, the strain-rate tensor,
associated with the Navier-Stokes equations. This variable is called SHEAR in the output EXODUS II file.
The permissible values for this postprocessing option are:
yes |
Calculate the mean shear rate. |
no |
Do not calculate the mean shear rate. |
Technical Discussion¶
No Discussion.
Pressure Contours¶
Pressure contours = {yes | no}
Description / Usage¶
The hydrodynamic pressure is normally a field variable within Goma; however, it is often interpolated in finite element space with discontinuous basis functions (in order to satisfy the well-known LBB stability criterion, cf. Schunk, et al. 2002). This option enables interpolating and smoothing the hydrodynamic pressure to nodal values that most post-processors can deal with (e.g. BLOT, Mustafa). This variable is called PRESSURE in the output EXODUS II file.
The permissible values for this postprocessing option are:
yes |
Calculate the pressure contours. |
no |
Do not calculate the pressure contours. |
Technical Discussion¶
No Discussion.
References¶
SAND2001-3512J: Iterative Solvers and Preconditioners for Fully-coupled Finite Element Formulations of Incompressible Fluid Mechanics and Related Transport Problems, P. R. Schunk, M. A. Heroux, R. R. Rao, T. A. Baer, S. R. Subia and A. C. Sun. (March 2002)
Fill Contours¶
Fill contours = {yes | no}
Description / Usage¶
This card triggers the inclusion of the level set or VOF fill function as a nodal variable in the output EXODUS II file.
The nodal variable appears as FILL in the output EXODUS II file. This function is computed with the FILL equation (see EQ card).
The permissible values for this postprocessing option are:
yes |
Calculate the fill contours. |
no |
Do not calculate the fill contours. |
Examples¶
An example card requesting FILL contours be written to the EXODUS II file is:
Fill contours = yes
Technical Discussion¶
No Discussion.
References¶
GT-020.1: Tutorial on Level Set Interface Tracking in GOMA, February 27, 2001, T.A. Baer
Concentration Contours¶
Concentration contours = {yes | no}
Description / Usage¶
As of 2/9/02 this card is not necessary. If EQ = species_bulk card is active in any material, than the concentration contours are including as post-processing nodal variables in the output EXODUS II file.
Examples¶
No Examples.
Technical Discussion¶
No Discussion.
References¶
No References.
Stress Contours¶
Stress contours = {yes | no}
Description / Usage¶
This card allows the user to invoke the components of the stress tensor for all viscoelastic modes be included as nodal post-processing variables. Often times this is not desirable on long time-dependent runs because of the voluminous data that will appear in the output EXODUS II file. This variable is called csij_mode in the output EXODUS II file, where i and j indicate components of the stress tensor and mode indicates the desired viscoelastic mode; for example, cs23_4 represents the stress contour for the fifth mode of polymer stress component yz.
The permissible values for this postprocessing option are:
yes |
Calculate and include the stress-tensor components for all modes of viscoelasticity. |
no |
Do not calculate and include the stress-tensor components. |
These stresses become dependent variables if the Polymer Constitutive Equation card is given any model but the NOPOLYMER model.
Examples¶
An example card requesting viscoelastic stress components be written:
Stress contours = yes
Technical Discussion¶
No Discussion.
References¶
GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao
First Invariant of Strain¶
First Invariant of Strain = {yes | no}
Description / Usage¶
The strain tensor is associated with the deformation of the mesh. Its first invariant is its trace and represents the volume change in the small strain limit. This variable is called IE in the output EXODUS II file.
The permissible values for this postprocessing option are:
yes |
Calculate the first invariant. |
no |
Do not calculate the first invariant. |
Technical Discussion¶
Computation of the strain tensor \(\underline{E}\) in Goma is discussed on the Solid Constitutive Equation card. The trace is related to the divergence of the tensor, and hence related to a measure of volume change in a material.
It should be noted that the mesh strain is equivalent to the material strain for LAGRANGIAN mesh motion types. For ARBITRARY or TOTAL_ALE mesh motion types (see Mesh Motion card), the strain is strictly related to mesh and not the material.
References¶
No References.
Second Invariant of Strain¶
Second Invariant of Strain = {yes | no}
Description / Usage¶
The strain tensor is associated with the deformation of the mesh. Its second invariant indicates the level of shear strain of the mesh. This variable is called IIE in the output EXODUS II file.
The permissible values for this postprocessing option are:
yes |
Calculate the second invariant. |
no |
Do not calculate the second invariant. |
Technical Discussion¶
The second invariant is computed in Goma as
Here Einstein’s summation convention applies, viz.
Third Invariant of Strain¶
Third Invariant of strain = {yes | no}
Description / Usage¶
The strain tensor is associated with the deformation of the mesh. Its third invariant indicates the volume change from the stress-free state (IIIE = 1.0 indicates no volume change). This variable is called IIIE in the output EXODUS II file.
The permissible values for this postprocessing option are:
yes |
Calculate the third invariant. |
no |
Do not calculate the third invariant. |
Technical Discussion¶
The mathematical definition of the third invariant is related to the determinant of the strain tensor, which is defined for the various constitutive equations in the manual entry for the Solid Constitutive Equation card.
References¶
No References.
Velocity Divergence¶
Velocity Divergence = {yes | no}
Description / Usage¶
The divergence of velocity is associated with local mass conservation or how well the solenoidal character of the velocity field in ARBITRARY mesh motion regions is being maintained. (Fluid momentum equations are only applied for this Mesh Motion option.) Here we calculate the \(L_2\) norm of the divergence of velocity so that it is always zero or positive. This variable is called DIVV in the output EXODUS II file.
The permissible values for this postprocessing option are:
yes |
Calculate the velocity divergence. |
no |
Do not calculate the velocity divergence. |
Technical Discussion¶
The divergence of the fluid velocity field is defined as the scalar \(\Delta\) • \(\underline{v}\).
References¶
No References.
Particle Velocity Divergence¶
Particle Velocity Divergence = {yes | no}
Description / Usage¶
This option is currently disabled. As of 2/16/2002, the multiphase particle momentum equation is deactivated. It is not recommended that this option be selected.
Examples¶
No Examples.
Technical Discussion¶
No Discussion.
References¶
No References.
Total Velocity Divergence¶
Not activated (PRS 2/16/02)
Description / Usage¶
Not currently activated. (2/16/02)
Examples¶
No Examples.
Technical Discussion¶
No Discussion.
Electric Field¶
Electric Field = {yes | no}
Description / Usage¶
The electric field vector components are written to the output EXODUS II file. The electric field is calculated as the negative gradient of the VOLTAGE field variable.
The permissible values for this postprocessing option are
yes |
Calculate the electric field vectors. |
no |
Do not calculate the electric field vectors. |
The vector components are called EX, EY, and (for three dimensional problems) EZ in the output EXODUS II file.
Examples¶
The following is a sample input card to calculate the Electric Field vector components:
Electric Field = yes
Technical Discussion¶
See also the Electric Field Magnitude post processing option.
References¶
No References.
Electric Field Magnitude¶
Electric Field Magnitude = {yes | no}
Description / Usage¶
The magnitude of the electric field is written to the output EXODUS II file. The electric field is calculated as the negative gradient of the VOLTAGE field variable.
The permissible values for this postprocessing option are:
yes |
Calculate the electric field magnitude. |
no |
Do not calculate the electric field magnitude. |
The electric field magnitude is called EE in the output EXODUS II file.
Examples¶
The following is a sample input card to calculate the Electric Field Magnitude:
Electric Field Magnitude = yes
Technical Discussion¶
See also the Electric Field post processing option.
References¶
No References.
Enormsq Field¶
Enormsq Field = {yes | no}
Description / Usage¶
This norm is based on the ENORM field variable (which, in turn, is derived from the VOLTAGE field variable).
The permissible values for this postprocessing option are:
yes |
Calculate the norm. |
no |
Do not calculate the norm. |
The field is stored in GENS0, GENS1, and GENS2 (if 3D) in the output EXODUS II file.
Technical Discussion¶
This post-processing variable is equal to \(\underline{\Delta}\) \(enorm^2\) . This, in turn, should approximate \(\underline{\Delta}\) \(\mid\) ( \(\underline{\Delta}V\) \(\mid^2\) ).
See also the Enormsq Field Norm post processing option.
References¶
No References.
Enormsq Field Norm¶
Enormsq Field Norm = {yes | no}
Description / Usage¶
This norm is based on the ENORM field variable (which, in turn, is derived from the VOLTAGE field variable).
The permissible values for this postprocessing option are:
yes |
Calculate the norm. |
no |
Do not calculate the norm. |
The norm is called GENSNORM in the output EXODUS II file.
Technical Discussion¶
This post-processing variable is equal to \(\underline{\Delta}\) \(enorm^2\) . This, in turn, should approximate \(\underline{\Delta}\) \(\mid\) ( \(\underline{\Delta}V\) \(\mid^2\) ).
See also the Enormsq Field post processing option.
References¶
No References.
Viscosity¶
Viscosity = {yes | no}
Description / Usage¶
This option allows you to plot the viscosity, which is written to the Output EXODUS II file as the variable MU. This is a useful feature for non-Newtonian fluids such as Phillip’s model for suspensions, Bingham plastic models, polymerizing solutions and other materials for which the viscosity may change orders of magnitude, greatly affecting the velocity and pressure fields. Contouring this variable MU over the domain can be useful in explaining some physical phenomena.
he permissible values for this postprocessing option are:
yes |
Calculate the viscosity and output as a nodal variable in the Output EXODUS II file. |
no |
Do not calculate the viscosity. |
Technical Discussion¶
See the material file Viscosity card for an explanation of the models for which the viscosity is variable and dependent on the flow field and other variables.
Density¶
Density = {yes | no}
Description / Usage¶
This card is used to trigger the thermophysical or mechanical property of density (see Density card) to be computed and output as an EXODUS II nodal variable in the Ouput EXODUS II file with the variable name RHO.
The permissible values for this postprocessing option are:
yes |
Calculate the density and store it as a nodal variable in the output EXODUS II file. |
no |
Do not calculate density. |
Examples¶
This is an example of the input to request density be written to the EXODUS II file.
Density = yes
Technical Discussion¶
No Discussion.
References¶
No References.
Lame MU¶
Lame MU = {yes | no}
Description / Usage¶
This option allows you to plot the Lame MU mechanical property, which is written to the Output EXODUS II file as the variable LAME_MU. This is a useful feature for temperature dependent mechanical properties and the like. Contouring this variable LAME_MU over the domain can be useful in explaining some physical phenomena.
The permissible values for this postprocessing option are:
yes |
Calculate the Lame MU and output as a nodal variable in the Output EXODUS II file. |
no |
Do not calculate the the coefficient (default). |
Examples¶
The following sample card requests LAME_MU be written to the EXODUS II file:
Lame MU = yes
Technical Discussion¶
No Discussion.
References¶
No References.
Lame LAMBDA¶
Lame LAMBDA = {yes | no}
Description / Usage¶
This option allows you to plot the Lame LAMDA mechanical property, which is written to the Output EXODUS II file as the variable LAMBDA. This is a useful feature for temperature dependent mechanical properties and the like. Contouring this variable LAMBDA over the domain can be useful in explaining some physical phenomena.
The permissible values for this postprocessing option are:
yes |
Calculate the Lame LAMBDA and output as a nodal variable in the Output EXODUS II file. |
no |
Do not calculate the the coefficient (default). |
Examples¶
The following sample card requests LAMBDA be written to the EXODUS II file:
Lame LAMBDA = yes
Technical Discussion¶
No Discussion.
References¶
No References.
Von Mises Strain¶
Von Mises Strain = {yes | no}
Description / Usage¶
This option allows you to plot the Von Mises strain invarients of the strain tensor, for use with the FAUX_PLASTICITY model of the modulus. These quantities are written to the Output EXODUS II file.
The permissible values for this postprocessing option are:
yes |
Calculate the von Mises strain invariants and output as a nodal variable in the Output EXODUS II file. |
no |
Do not calculate the invariants (default). |
Examples¶
The following sample card requests LAMBDA be written to the EXODUS II file:
Von Mises Strain = yes
Technical Discussion¶
No Discussion.
References¶
No References.
Von Mises Stress¶
Von Mises Stress = {yes | no}
Description / Usage¶
This option allows you to plot the Von Mises stress tensor invarients, for use with the FAUX_PLASTICITY model of the modulus. These quantities are written to the Output EXODUS II file.
The permissible values for this postprocessing option are:
yes |
Calculate the von Mises stress invariants and output as a nodal variable in the Output EXODUS II file. |
no |
Do not calculate the invariants (default). |
Examples¶
The following sample card requests LAMBDA be written to the EXODUS II file:
Von Mises Stress = yes
Technical Discussion¶
No Discussion.
Moving Mesh Residuals¶
Moving Mesh Residuals = {yes | no}
Description / Usage¶
These nodal variables are constructed from the corresponding weighted residual functions of the solid momentum equations (activated with the EQ = mesh* cards). The weighted residuals are formed using a Galerkin finite-element formulation. In the output EXODUS II file they appear as nodal variables RDX, RDY, and RDZ, corresponding to each of the independent components of the solid momentum balance (both pseudo and real).
The permissible values for this postprocessing option are:
yes |
Include the moving mesh residuals as nodal variables in the ouput EXODUS II file. |
no |
Do not include moving mesh residuals. |
Examples¶
Following is a sample card which does not activate writing of mesh residuals:
Moving Mesh Residuals = no
Technical Discussion¶
This option can be used to help understand convergence behavior of a particular problem, as it allows the user to visualize the pattern of residuals over the computational domain during a Newton iteration process. The intermediate solutions of a Newton iteration process can be activated with the Write Intermediate Results card. Contouring these residuals can indicate where the convergence of a problem is being delayed, and give the user/developer some clues as to the boundary condition or local region of the mesh which is responsible.
Mass Diffusion Vectors¶
Mass Diffusion Vectors = {yes | no}
Description / Usage¶
Activating this post-processing option allows the user to visualize the diffusive mass flux directions of all species components in a problem. Species components result from the EQ = species_bulk equation card. With this option selected, the output EXODUS II file will contain nodal variables called Y0dif0 (diffusion of first species in x direction), Y0dif1 (diffusion of first species in y direction), Y0dif2 (diffusion of first species in z direction), Y1dif0 (diffusion of second species in x direction), Y2dif1 (diffusion of second species in y direction), … and so on, depending on the number of species components in the problem.
The permissible values for this postprocessing option are:
yes |
Calculate the mass diffusion vectors and include in the output EXODUS II file. |
no |
Do not calculate the mass diffusion vectors. |
Technical Discussion¶
Currently this option is available only for FICKIAN and HYDRODYNAMIC mass flux types (see Diffusion Constitutive Equation card). In the FICKIAN case, the flux is computed with the base, constant diffusivity.
References¶
No References.
Diffusive Mass Flux Vectors¶
Diffusive Mass Flux Vectors = {yes | no}
Description / Usage¶
Please see description for Mass Diffusion Vectors card; this card performs exactly the same function.
Examples¶
This card turns on writing of diffusive mass flux vectors to the EXODUS II file:
Diffusive Mass Flux Vectors = yes
Technical Discussion¶
Please see description for Mass Diffusion Vectors card.
References¶
No References.
Mass Fluxlines¶
Mass Fluxlines = {yes | no}
Description / Usage¶
With this post-processing option mass-diffusion pathlines are calculated and stored as post-processing nodal variables in the output EXODUS II file. This variables are called Y0FLUX, Y1FLUX, …(by species number) in the file and can be contoured in the visualization program. These flux lines are analogous to the stream function, viz. contours of the flux function represent pathlines for each species in solution.
The permissible values for this postprocessing option are:
yes |
Calculate the mass fluxlines and include in the output EXODUS II file. |
no |
Do not calculate the mass fluxlines. |
Examples¶
The following sample card requests that mass-diffusion pathlines be written to the EXODUS II file:
Mass Fluxlines = yes
Technical Discussion¶
Currently this option is available only for FICKIAN and HYDRODYNAMIC mass flux types (see Diffusion Constitutive Equation card). In the FICKIAN case, the flux is computed with the base, constant diffusivity. Also, the Mass Diffusion Vectors post processing option must also be activated for this option to work.
References¶
No References.
Energy Conduction Vectors¶
Energy Conduction Vectors = {yes | no}
Description / Usage¶
Activation of this option can be used to visualize the energy conduction paths in a solution. The resulting nodal variables are called TCOND0 (conduction in x direction), TCOND1 (conduction in y direction), and TCOND2 (conduction in z direction) in the output EXODUS II file.
The permissible values for this postprocessing option are:
yes |
Calculate the energy conduction vectors and store in the output EXODUS II file. |
no |
Do not calculate the energy conduction vectors. |
Examples¶
This example card requests that energy conduction vectors be written to the EXODUS II file:
Energy Conduction Vectors = yes
Technical Discussion¶
These quantities can be employed in a hedge-hog or vector plot to visualize the energy conduction pathways across a domain (cf. the vector option in BLOT, or the hedge-hog option in Mustafa, for example).
References¶
No References.
Energy Fluxlines¶
Energy Fluxlines= {yes | no}
Description / Usage¶
This post-processing option triggers the energy fluxlines to be calculated. The energy flux function is analogous to the stream function, its contours representing paths of energy flow through the domain. This variable is called TFLUX in the output EXODUS II file.
The permissible values for this postprocessing option are:
yes |
Calculate and write the energy fluxlines to the output EXODUS II file. |
no |
Do not calculate the energy fluxlines. |
Technical Discussion¶
The Energy Conduction Vectors must also be activated for this post processing option to work.
References¶
No References.
Time Derivatives¶
Time Derivatives = {yes | no}
Description / Usage¶
This option enables writing the time derivative of all the field variables as nodal variables to the output EXODUS II file. These variables are labeled XDOT0 (mesh velocity in x direction), XDOT1 (mesh velocity in y direction), XDOT2 (mesh velocity in z direction), VDOT0 (fluid acceleration in x direction), VDOT1 (fluid acceleration in y direction), VDOT2 (fluid acceleration in z direction), TDOT (rate of temperature change), Y0DOT (rate of 1st species concentration change), Y1D0T (rate of second species concentration change), and so on. The quantities can then be contoured or displayed by some other means with a visualization or graphics package.
The permissible values for this postprocessing option are:
yes |
Calculate the time derivatives and write them as nodal variables in the output EXODUS II file. |
no |
Do not calculate the time derivatives. |
Examples¶
The following sample card requests that time derivatives be written to the EXODUS II file:
Time Derivatives = yes
Technical Discussion¶
Currently, this routine uses the values in the global vector xdot to report this data. During the first time step, all the xdot values are zero; by the second time step, these data should be realistic.
References¶
No References.
Mesh Stress Tensor¶
Mesh Stress Tensor = {yes | no}
Description / Usage¶
The mesh stress tensor is associated with the equations of elasticity. The stress tensor has six entries (in three dimensions, because it is symmetric) called T11, T22, T33, T12, T13, and T23 in the output EXODUS II file.
The permissible values for this postprocessing option are:
yes |
Calculate the mesh stress tensor and write to output EXODUS II file. |
no |
Do not calculate the mesh stress tensor. |
Examples¶
The following sample card turns on the writing of the stress tensor to the EXODUS II file:
Mesh Stress Tensor = yes
Technical Discussion¶
The defining constitutive equations for these stresses can be found in the description for the Solid Constitutive Equation card. This option applies to all solid-material types (see Mesh Motion card), viz. TOTAL_ALE, LAGRANGIAN, ARBITRARY, DYNAMIC_LAGRANGIAN. In the TOTAL_ALE and ARBITRARY mesh motion types, the mesh stress is exactly that and not the true stress of the material. For TOTAL_ALE mesh motion types, use Real Solid Stress Tensor option to get the true solid material stresses.
References¶
No References.
Real Solid Stress Tensor¶
Real Solid Stress Tensor = {yes | no}
Description / Usage¶
The real solid stress tensor is associated with the equations of elasticity. If the mesh motion is of LAGRANGIAN type, then these quantities are not available; if is of TOTAL_ALE type, they are available. The stress tensor has six entries (in three dimensions because it is symmetric) called T11_RS, T22_RS, T33_RS, T12_RS, T13_RS, and T23_RS in the output EXODUS II file.
The permissible values for this postprocessing option are:
yes |
Calculate the real solid stress tensor and write to the output EXODUS II file. |
no |
Do not calculate the real solid stress tensor. |
Examples¶
No stress tensor is written for the following sample input card:
Real Solid Stress Tensor = no
Technical Discussion¶
This option is applicable only to TOTAL_ALE mesh motion types (see Mesh Motion card). Compare this with Mesh Stress Tensor post processing option for other types of mesh motion.
References¶
No References.
Mesh Strain Tensor¶
Mesh Strain Tensor = {yes | no}
Description / Usage¶
The mesh strain tensor is associated with the equations of elasticity. The strain tensor has six entries (in three dimensions, because it is symmetric) called E11, E22, E33, E12, E13, and E23 in the output EXODUS II file, corresponding to the six independent components (the numbers 1, 2, and 3 indicate the basis direction, e.g. 1 means xdirection for a Cartesian system).
The permissible values for this postprocessing option are:
yes |
Calculate the mesh strain tensor and write the components as nodal variables to the output EXODUS II file. |
no |
Do not calculate the mesh strain tensor. |
Examples¶
The following example input card does not request output of the stain tensor:
Mesh Strain Tensor = no
Technical Discussion¶
Definitions of the strain tensor depend on the solid constitutive equation type (see description for Solid Constitutive Equation card).
References¶
No References.
Viscoplastic Def_Grad Tensor¶
Viscoplastic Def_Grad Tensor = {yes | no}
Description / Usage¶
The components of this tensor are associated with the elasto-viscoplasticity model, (described in detail in Schunk, et. al., 2001). If the mesh motion is of LAGRANGIAN type, then this card activates the components of this tensor to be available in the postprocessing EXODUS II file (see Mesh Motion card). The components are called FVP11, FVP12, FVP21, FVP22, and FVP33. This tensor is the identity tensor in regions that have not yielded, and so the diagonal components are unity; in regions that have yielded, these components deviate from the identity. Contouring them can reveal regions of plastic flow.
The permissible values for this postprocessing option are:
yes |
Calculate the viscoplastic Def_Grad tensor and write components in the output EXODUS II file. |
no |
Do not calculate the viscoplastic Def_Grad tensor. |
Examples¶
This sample input card does not activate Def_Grad output to the EXODUS II file:
Viscoplastic Def_Grad Tensor = no
Technical Discussion¶
Please see complete discussion in Schunk, et. el. (2001).
References¶
GT-019.1: Elastoviscoplastic (EVP) Constitutive Model in GOMA: Theory, Testing, and Tutorial, P. R. Schunk, A. Sun, S. Y. Tam (Imation Corp.) and K. S. Chen, January 11, 2001
Lagrangian Convection¶
Lagrangian Convection = {yes | no}
Description / Usage¶
In deformable solids with a Lagrangian mesh, convection in the stress-free state can be mapped to the deformed configuration; this variable stores the velocity vectors of this solid motion (see Convective Lagrangian Velocity card). This variable is called VL1, VL2, VL3 in the output EXODUS II file; the integer values 1, 2 and 3 denote coordinate directions.
The permissible values for this postprocessing option are:
yes |
Calculate the Lagrangian convection and store as nodal variable velocity fields in the output EXODUS II file. |
no |
Do not calculate the Lagrangian convection. |
Technical Discussion¶
This option only applies to Mesh Motion type of LAGRANGIAN.
References¶
No References.
Normal and Tangent Vectors¶
Normal and Tangent Vectors = {yes | no}
Description / Usage¶
This option allows one to write the values of the normal and tangent vectors used in rotating the mesh and momentum equations as nodal variables to the output EXODUS II file. In two-dimensional problems, the normal and tangent vectors are saved as N1, N2, N3 and T1, T2, T3 in the output EXODUS II file; in two dimensions these vectors are calculated at all the nodes. In three-dimensional problems, the normal and tangent vectors are saved as N1, N2, N3, TA1, TA2, TA3, and TB1, TB2, TB3; in three dimensions, these vectors only exist at nodes with rotation specifications, and the vectors correspond to the rotation vectors chosen by the ROT Specifications for the given node (see description for ROT cards). Thus in three-dimensional problems, vectors are not necessarily saved for every node, nor do the vectors necessarily correspond to the normal, first tangent, and second tangent, respectively.
The permissible values for this postprocessing option are:
yes |
Calculate the vectors and store as nodal variables in the output EXODUS II file. |
no |
Do not calculate the vectors. |
Examples¶
The following sample card produces no output to the EXODUS II file:
Normal and Tangent vectors = no
Technical Discussion¶
This option is mostly used to debug three-dimensional meshes for full threedimensional ALE mesh motion. The tangent fields in 3D should be smooth across the surfaces, and Goma takes many steps to make them so. The surface normal crossed into any vector that is different will produce one tangent vector. Then the normal crossed (viz. cross product of two vectors) with the first tangent will produce a second tangent vector. Because the surface tangent basis fields are not unique, they must be uniform over a surface when the rotated Galerkin weighted residuals are formed (see description for ROT cards). Imperfections or defects in the mesh can lead to nonsmooth fields.
References¶
GT-018.1: ROT card tutorial, January 22, 2001, T. A. Baer
Error ZZ Velocity¶
Error ZZ velocity = {yes | no}
Description / Usage¶
This option has been disabled for lack of use, but originally allowed the user to compute a posteriori error estimates in the velocity field from the Zienkiewicz-Zhu energy norm error measure.
Examples¶
No Examples.
Technical Discussion¶
No Discussion.
References¶
No References.
Error ZZ Heat Flux¶
Error ZZ heat flux = {yes | no}
Description / Usage¶
This option has been disabled for lack of use, but originally allowed the user to compute a posteriori error estimates in the computed temperature/energy flux field from the Zienkiewicz-Zhu energy norm error measure.
Examples¶
No Examples.
Technical Discussion¶
No Discussion.
References¶
No References.
Error ZZ Pressure¶
Error ZZ pressure = {yes | no}
Description / Usage¶
This option has been disabled for lack of use, but originally allowed the user to compute a posteriori error estimates in the pressure field from the Zienkiewicz-Zhu energy norm error measure.
Examples¶
No Examples.
Technical Discussion¶
No Discussion.
References¶
No References.
User-Defined Post Processing¶
User-Defined Post Processing = {yes | no} <float_list>
Description / Usage¶
This option enables user-defined postprocessing options in Goma. An arbitrary number of floating point constants can be loaded to use in the user-defined subroutine user_post (user_post.c). This variable is called USER in the output EXODUS II file and can be contoured or processed just like any other nodal variable in a postprocessing visualization package.
yes |
Calculate and write the user-defined postprocessing variable to the output EXODUSII file. |
no |
Do not calculate the user-defined postprocessing. |
<float_list> |
An arbitrary number (including zero) of floating point numbers, which can be accessed in file user_post |
Examples¶
Consider the following sample input card:
User-Defined Post Processing = yes 100.
Suppose you would like to contour the speed of a fluid in a two-dimensional problem using this card, with your intent being to multiply the calculated value by a factor of 100.0 for some unit conversion or something. You must add
post_value = param[0]*sqrt(fv->v[0]*fv->v[0] + fv->v[1]*fv->*v[1]) ;
to user_post.c. Note also that you have to comment out the error handler line just above the location you enter the post_value code. The comments in the routine help guide you through the process.
Technical Discussion¶
See the function user_post in user_post.c.
Porous Saturation¶
Porous Saturation = {yes | no}
Description / Usage¶
In partially saturated porous media, the saturation represents the volume fraction of the pore space that is filled with liquid. If this option is selected, then the saturation level (an auxiliary variable) is included in the output EXODUS II file. This variable is called SAT in the output EXODUS II file.
The permissible values for this postprocessing option are:
yes |
Calculate the porous saturation and write to the output EXODUS II file. |
no |
Do not calculate the porous saturation. |
Examples¶
This sample input card turns off writing of saturation to the EXODUS II file:
Porous Saturation = no
Technical Discussion¶
No Discussion.
References¶
GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk
GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk
SAND96-2149: Drying in Deformable Partially-Saturated Porous Media: Sol-Gel Coatings, Cairncross, R. A., P. R. Schunk, K. S. Chen, S. S. Prakash, J. Samuel, A. J. Hurd and C. Brinker (September 1996)
Total Density of Solvents in Porous Media¶
Total density of solvents in porous media = {yes | no}
Description / Usage¶
This post processing option can be used to trigger the computation and output of the total density of solvents as a nodal field variable to the output EXODUS II file. Three nodal variables are written, Rho_Total_Liq, Rho_Total_air and Rho_Total_solid. The mathematical details are given below in the technical discussion. This option applies to media types of POROUS_SATURATED, POROUS_UNSATURATED, and POROUS_TWO_PHASE (see Media Type card). The options are:
yes |
Calculate and write the total solvent densities as a postprocessing variable to the output EXODUSII file. |
no |
Do not calculate the total solvent densities. |
Examples¶
Total density of solvents in porous media = yes
This card will result in the calculation and output of the mixture density of solvent (viz., phase mixture of liquid solvent in vapor form, liquid form, and the form adsorbed in the solid skeleton for partially saturated porous flows). The form of that mixture density is given in the technical discussion.
Technical Discussion¶
In saturated flow cases, viz. for Media Type selection POROUS_SATURATED, the total solvent density is
where \(\rho_1\) is the pure liquid density and \(\phi\) is the porosity. Here we have assumed that no liquid solvent is adsorbed into the solid struts (currently the assumption used throughout Goma).
For partially saturated flows, viz. for Media Type selection POROUS_UNSATURATED or POROUS_TWO_PHASE, the total density is given by
where \(\rho_{gv}\) is the density of solvent vapor in the total gas-solvent vapor mixture (see Density of solvents in gas phase in porous media card), S is the saturation (see Porous Saturation card), and \(\chi_{ls}\) is the volume fraction of solvent in liquid phase (including any condensed species component). When calculating the total density of the liquid (Rho_Total_liq), the liquid vapor density comes from a Kelvin vapor-liquid equilibrium relation. The total density of the gas phase (Rho_Total_gas) will use a vapor density fro air and a volume fraction of zero (0) since air is insoluble. The total density of the solid in the gas (Rho_Total_solid) is zero (0).
References¶
GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk
Density of Solvents in Gas Phase in Porous Media¶
Density of solvents in gas phase in porous media = {yes | no}
Description / Usage¶
This post processing option can be used to trigger the computation and output of the density of solvents in the gas phase only, including the volume occupied by the assumed insoluble gas (e.g. air), as a nodal field variable to the output EXODUS II file. The nodal variables are called RhoSolv_g_liq, RhoSolv_g_air and RhoSolv_g_solid. The mathematical details are given below in the technical discussion. This option applies to media types of POROUS_UNSATURATED, and POROUS_TWO_PHASE (see Media Type card). The options are:
yes |
Calculate and write the gas phase solvent density as a postprocessing variable to the output EXODUSII file. |
no |
Do not calculate the total solvent density. |
Examples¶
The following input card turns off writing solvent densities to the EXODUS II file:
Density of solvents in gas phase in porous media = no
Technical Discussion¶
The air and solid components are insoluble in the gas phase so the RhoSolv_g_air and RhoSolv_g_solid variables will be zero. The gas-density of liquid solvents (RhoSolv_g_liq) is determined from the vapor-liquid equilibrium relationship at a liquid-vapor meniscus. Specifically,
where \(M_w\) is the average molecular weight of solvents in the mixture, R is the ideal gas constant, T is the temperature, and \(\rho_v\) is the equilibrium vapor pressure. Note that this vapor pressure can be affected by local meniscus curvature through the Kelvin equation (cf. Schunk, 2002 and Porous Vapor Pressure card).
References¶
GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk
Density of Liquid Phase in Porous Media¶
Density of liquid phase in porous media = {yes | no}
Description / Usage¶
This post processing option can be used to trigger the computation and output of the density of solvents in the liquid phase only, averaged over the mixture, as a nodal field variable to the output EXODUS II file. The nodal variable is called Rho_Liq_Phase. The mathematical details are given below in the technical discussion. This option applies to media types of POROUS_SATURATED, POROUS_UNSATURATED, and POROUS_TWO_PHASE (see Media Type card). The options are:
yes |
Calculate and write the density of solvent in the liquid phase as a postprocessing variable to the output EXODUSII file. |
no |
Do not calculate the liquid solvent density. |
Examples¶
An example of an input card which activates writing of the density to the EXODUS II file is:
Density of liquid phase in porous media = yes
Technical Discussion¶
In liquid-saturated flow cases, viz. for Media Type selection POROUS_SATURATED, the total solvent density in the liquid phase is
where \(\rho_l\) is the pure liquid density and \(\phi\) is the porosity. Here we have assumed that no liquid solvent is adsorbed into the solid struts (currently the assumption used throughout Goma).
For partially saturated flows, viz. for Media Type selection POROUS_UNSATURATED or POROUS_TWO_PHASE, the density of solvent in the liquid phase only is given by
where S is the saturation (see Porous Saturation card). Compare this with the quantity computed with the Total density of solvents in porous media card.
References¶
GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk
Gas Phase Darcy Velocity in Porous Media¶
Gas phase Darcy velocity in porous media = {yes | no}
Description / Usage¶
This post-processing option will lead to the explicit calculation and storage of the Darcy velocity components in the gas phase, viz. the velocity of the gas phase due to gas-phase pressure gradients. This option is only available for POROUS_TWO_PHASE media types (cf. Media Type card). The velocity components appear in the output EXODUS II file as the nodal variables Darcy_Vel_g_0, Darcy_Vel_g_1 and Darcy_Vel_g_2.
The permissible values for this postprocessing option are:
yes |
Calculate the gas-phase Darcy velocity components and write to the output EXODUSII file. |
no |
Do not calculate the gas phase velocity components. |
Examples¶
This input example turns on calculation of the gas phase velocity components:
Gas phase Darcy velocity in porous media =yes
Technical Discussion¶
The gas-phase Darcy velocity is given by the extended Darcy law, which accounts for the relative reduced flow due to the presence of another phase, viz.
Here \(\nu_g\) represents the Darcy flux, or Darcy velocity, in the gas phase, k is the permeability of the porous medium, \(k_g\) is the relative permeabilities for the gas and liquid phases respectively, \(\mu_g\) are the gas viscosity, \(p_g\) is the pressure in the gas phase, and g is the gravitational force vector. \(\rho_g\) is the density of the gas phase and is equal to the sum of the partial densities of air and solvent vapor,
References¶
GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk
Liquid Phase Darcy Velocity in Porous Media¶
Liquid phase Darcy velocity in porous media = {yes | no}
Description / Usage¶
This post-processing option will lead to the explicit calculation and storage of the Darcy velocity components in the liquid phase, viz. the velocity of the liquid phase due to liquid phase pressure gradients. This option is available for all porous media types (cf. Media Type card). The velocity components appear in the output EXODUS II file as the nodal variables Darcy_Vel_l_0, Darcy_Vel_l_1 and Darcy_Vel_l_2.
The permissible values for this postprocessing option are:
yes |
Calculate the liquid-phase Darcy velocity components and write to the output EXODUSII file. |
no |
Do not calculate the liquid phase velocity components. |
Examples¶
This input example turns on calculation of the liquid phase velocity components:
Liquid phase Darcy velocity in porous media = yes
Technical Discussion¶
The liquid-phase Darcy velocity is given by the extended Darcy law, which accounts for the relative reduced flow due to the presence of another phase, viz.
Here \(v_l\) represents the Darcy flux, or Darcy velocity, in the gas phase, k is the permeability of the porous medium, \(k_l\) is the relative permeabilities for the liquid and liquid phases respectively, \(\mu_l\) are the liquid viscosity, \(p_l\) is the pressure in the liquid phase, and g is the gravitational force vector. \(\rho_l\) is the density of the liquid phase.
References¶
GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk
Capillary Pressure in Porous Media¶
Capillary pressure in porous media = {yes | no}
Description / Usage¶
In partially saturated porous media, the capillary pressure is the difference between the gas and liquid pressures. This option only takes affect for POROUS_TWO_PHASE and POROUS_UNSATURATED media types (see Media Type card). This variable is called PC in the output EXODUS II file.
The permissible values for this postprocessing option are:
yes |
Calculate the capillary pressure and write to output EXODUS II file. |
no |
Do not calculate the capillary pressure. |
Examples¶
This is a sample input card to activate calculation of capillary pressure:
Capillary pressure in porous media = yes
Technical Discussion¶
The capillary pressure is a critical variable for partially saturated porous media, and is in fact the dependent variable for unsaturated (not two-phase) flows for which the gasphase pressure is taken as constant. It is simply defined as
As such, positive capillary pressures imply liquid phase pressure being greater than gas phase pressure. Because liquid phase saturation strongly correlates to capillary pressure, this current quantity is a good indicator of the level of liquid inventory in smaller pores in the skeleton relative to large pores. Contouring this quantity can give some indication of the level of suction exerted on the porous-skeleton, which is relevant when the skeleton is taken as deformable.
References¶
GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk
Grid Peclet Number in Porous Media¶
Grid Peclet Number in porous media = {yes | no}
Description / Usage¶
This option triggers the computation and output of the so-called grid-level Peclet number as a nodal variable in the output EXODUS II file. It appears as a nodal variable called Por_Grid_Peclet. This quantity gives the user a measure of advective transport relative to diffusive transport in a porous medium, and is strongly correlated to the steepness of a saturation front. This quantity is actually used to scale the formulation which employs the streamline upwind Petrov-Galerkin method for stabilizing the equations for partially saturated flow. This option only applies for unsaturated media and only for the SUPG option on the Porous Weight Function card.
The permissible values for this postprocessing option are:
yes |
Compute the grid-level Peclet Number and write to output EXODUS II file. |
no |
Do not calculate the grid-level Peclet Number. |
Examples¶
This is a sample input card to activate calculation of the Peclet Number:
Grid Peclet Number in porous media = yes
Technical Discussion¶
See discussion for the Porous Weight Function card.
References¶
GTM-029.0: SUPG Formulation for the Porous Flow Equations in Goma, H. K. Moffat, August 2001 (DRAFT).
SUPG Velocity in Porous Media¶
SUPG Velocity in porous media = {yes | no}
Description / Usage¶
Used to specify use of effective velocities in SUPG formulations for porous media. It is written to the output EXODUS II file as nodal variable U_supg_porous.
The permissible values for this postprocessing option are:
yes |
Calculate and write the effective velocity components as a postprocessing variable to the output EXODUSII file. |
no |
Do not calculate the effective velocity components. |
Examples¶
This is a sample input card to activate calculation of SUPG Velocity:
SUPG Velocity in porous media = yes
Technical Discussion¶
No Discussion.
References¶
GTM-029.0: SUPG Formulation for the Porous Flow Equations in Goma, H. K. Moffat, August 2001 (DRAFT).
Vorticity Vector¶
Vorticity Vector = {yes | no}
Description / Usage¶
This option allows the user to output the vorticity vector to the output EXODUS II file. It applies to problems with the fluid momentum equations (see EQ = momentum* cards). The output nodal variables are named VORTX, VORTY, VORTZ.
The permissible values for this postprocessing option are:
yes |
Calculate the vorticity vectors and store in the output EXODUS II file. |
no |
Do not calculate the vorticity vectors. |
Examples¶
This example card requests that vorticity vectors be written to the EXODUS II file:
Vorticity Vector = yes
Technical Discussion¶
The vorticity vector function, \(\underline\omega\) , is defined in terms of the velocity \(\underline\upsilon\) as: