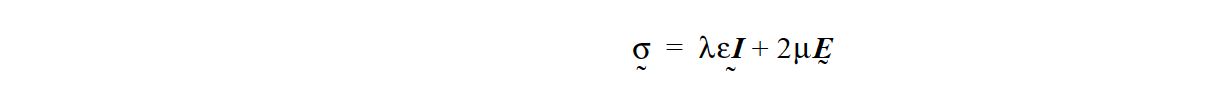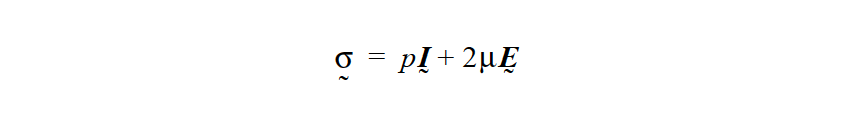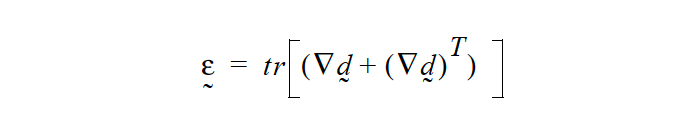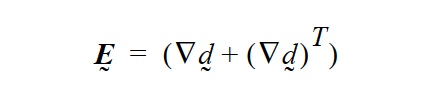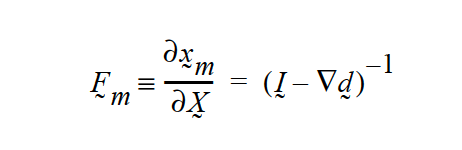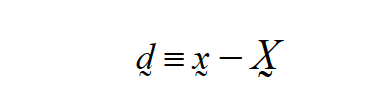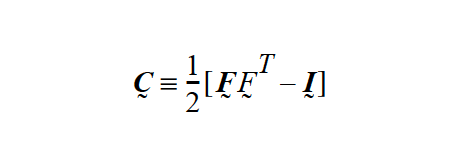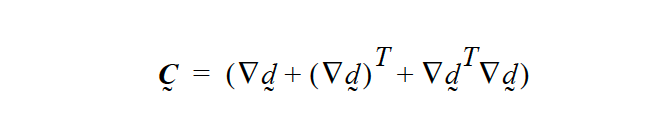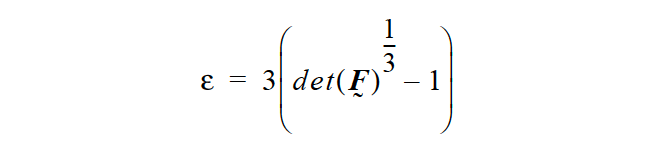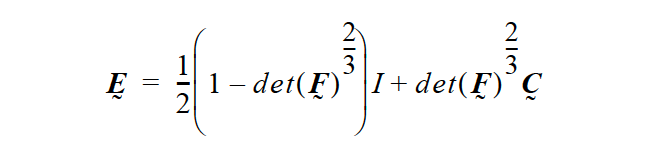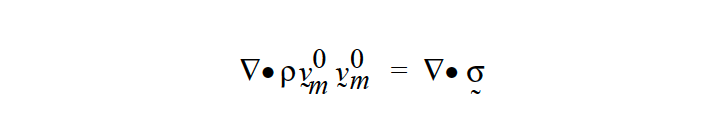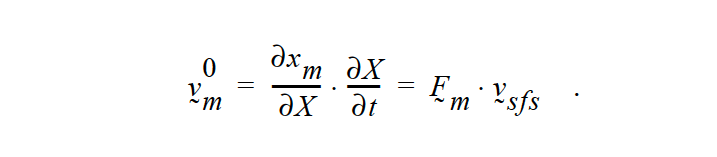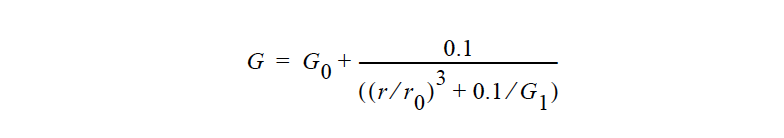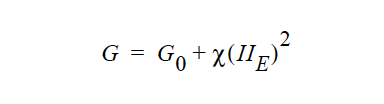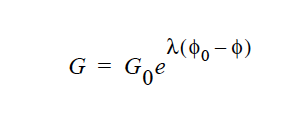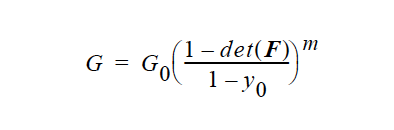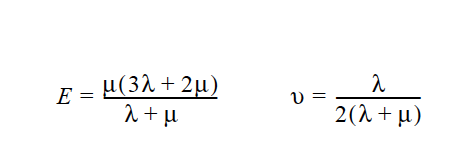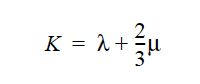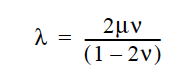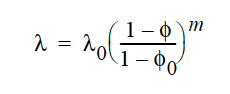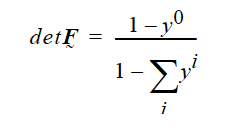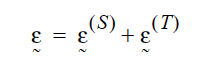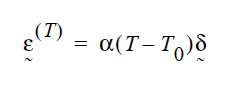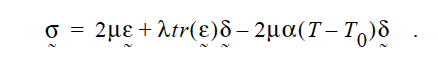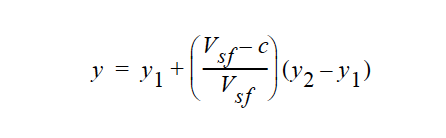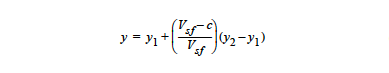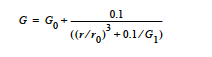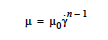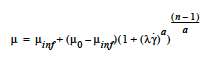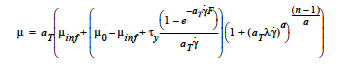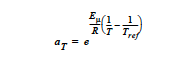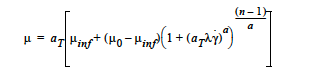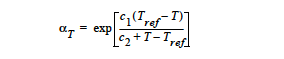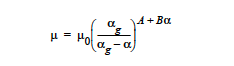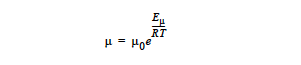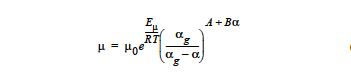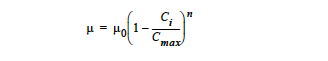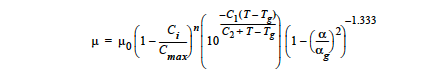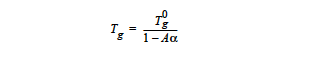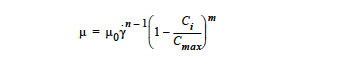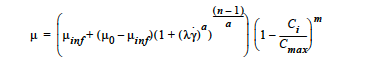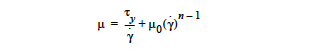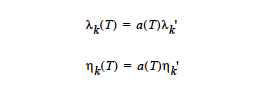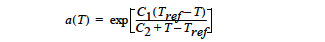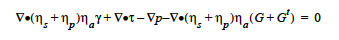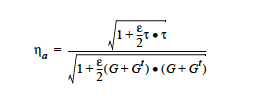Mechanical Properties and Constitutive Equations¶
This section of the material property input specifies the type of model, for both solids and fluids, that relates stress and strain (or strain-rate) as well as the various parameters for these models. Models for solids are relatively simple compared to solid mechanics codes but cover the primary needs in fluid-solid problems. The models for fluids are quite extensive, covering Newtonian, generalized-Newtonian, rate-dependent models, thermally-dependent models, curing and particleladen models and combinations of these. These properties are used in the solid and fluid momentum conservation equations.
Solid Constitutive Equation¶
Solid Constitutive Equation = {model_name}
Description / Usage¶
This required card specifies the constitutive equation used to control mesh motion and/ or the constitutive model describing solid material stress response to deformation. The single input parameter is defined as
{model_name} |
The name of the constitutive equation. The permissible values for {model_name} are dependent on the selection for the Mesh Motion type, that being one of ARBITRARY, LAGRANGIAN/DYNAMIC_LAGRANGIAN, or TOTAL_ALE. For an ARBITRARY Mesh Motion, {model_name} can be one of the following:
For a LAGRANGIAN, DYNAMIC_LAGRANGIAN, or TOTAL_ALE Mesh Motion, {model_name} can be one of the following:
|
The functional form of each of these equations is provided in the Technical Discussion with some important details.
Examples¶
The following is a sample input card:
Solid Constitutive Equation = LINEAR
This equation type requires two elastic constants be specified, Lame Lambda and Lame Mu. This constitutive equation can be used for all Mesh Motion types. It is not recommended for large mesh deformations, even for ALE problems, because of spurious stresses generated by solid body translation or rotation.
Technical Discussion¶
The general compressible form of Hooke’s Law, which applies to the LINEAR, NONLINEAR and HOOKEAN_PSTRAIN options, can be written as
Here \(\lambda\) is the Lame coefficient for volume expansion, \(\varepsilon\) is the volume strain measure whose definition depends on the model chosen, \(\mu\) is another elastic Lame coefficient for shear deformation, \(\underline {E}\) and is the chosen strain tensor, the form of which also depends on the constitutive model chosen.
The general incompressible form of Hooke’s Law, which applies to all INCOMP* options, can be written as:
with p being the solid phase pressure. An additional continuity equation is required in this case to account for the pressure (see Continuity equation card). Note, for these model options one must set the Lame LAMBDA coefficient to zero, or the pressure term and the expansion term are added together.
The volume change and strain tensors depend on the chosen solid constitutive equation and are as follows:
For the LINEAR option:
and
where \(\underline {d}\) is the displacement field vector, tr is the tensor trace operator, and the gradient operator (\(\Delta\)) is with respect to the deformed coordinates.
For all NONLINEAR models, we use the deformation gradient tensor as a building block:
The “material coordinates” are \(\underline {X}\) and describe the original locations of all parcels of material in the domain; and the “current configuration/spatial coordinates” \(\underline {x}\) are the deformed mesh coordinates. Of course we have
for all LAGRANGIAN mesh motion cases. We define a Cauchy-Green tensor as:
and invoke the linearized small strain theory (viz. that \(\Delta_x\) \(\underline{d}\) \(\equiv\) \(\Delta_x\) \(\underline {d}\)), and write
With these quantities, we form the volume strain and strain tensor for the various models:
For NONLINEAR, INCOMP_PSTRAIN, INCOMP_3D, and HOOKEAN_PSTRAIN:
For INCOMP_PSTRAIN and INCOMP_3D we use:
For all other models we use \(\underline {E}\) = \(\underline {C}\). It is noteworthy that we use the linearized small strain theory for parts of the strain tensor, but the real Lagrangian deformation gradient for the volumetric strain. For elastoviscoplastic models and TOTAL_ALE solid mechanics, we do not invoke the linearized small strain theory.
Also noteworthy is that the elastic constants \(\lambda\) and \(\mu\) are related to the more well known bulk and Young’s moduli and the Poisson’s ratio by simple expressions (see Lame Mu and Lame Lambda cards).
Theory¶
The incompressible options (i.e., INCOMP_PSTRAIN and INCOMP_PSTRESS and INCOMP_3D) use the theory of Segalman, et. al. (1992) to control mesh motion and couple the volume dilation to changes in solvent content. Plane strain implies that there is no deformation in the z-direction; plane stress implies there is no stress change in the z-direction.
References¶
GT-005.3: THE NEW TOTAL-ARBITRARY-LAGRANGIAN-EULERIAN (TALE) CAPABILITY and its applicability to coating with/on deformable media, August 6, 1999, P. R. Schunk
SAND2000-0807: TALE: An Arbitrary Lagrangian-Eulerian Approach to Fluid- Structure Interaction Problems, P. R. Schunk (May 2000)
SAND96-2149: Drying in Deformable Partially-Saturated Porous Media: Sol-Gel Coatings, Cairncross, R. A., P. R. Schunk, K. S. Chen, S. S. Prakash, J. Samuel, A. J. Hurd and C. Brinker (September 1996)
Segalman, D., W. Witkowski, D. Adolf, M. Shahinpoor, “Theory and Application of Electrically Controlled Polymeric Gels”, Smart Mater. Struct. 1:95-100 (1992).
Plasticity Equation¶
Plasticity Equation = {model_name} [ ]
Description / Usage¶
This optional card specifies the formulation for the potential yielding/plastic flow regime during solid deformation. This card is not to be used in place of the Solid Constitutive Equation card, but rather supplements that card to describe the constitutive behavior during plastic deformation. Elastic deformation still proceeds according to the model specified on the Solid Constitutive Equation card (i.e., for regimes that have not yielded). The single input parameter is defined as
{model_name} |
Name of the plasticity model. This parameter can have one of the following values: |
EVP_HYPER |
a constitutive equation that uses the elasticity portion specified on the Solid Constitutive Equation card for unyielding material and a complex hyperelastic plasticity equation for the yielding/flowing material as determined by the Von Mises yield criterion. |
NO_MODEL |
this, or any value other than EVP_HYPER, will result in no plastic deformation. |
Requirements for the use of this model are
Transient problems only
LAGRANGIAN mesh motion only; no TALE
Continuous media only; no porous media (as specified on the Media Type card)
Elastic Plane Strain models only (i.e., INCOMP_PSTRAIN in the Solid Constitutive Equation card)
a Plastic Viscosity card and an EVP Yield Stress card must also be supplied.
Examples¶
Following is a sample card:
Plasticity Equation = EVP_HYPER
which specifies hyperelastic elastoviscoplastic model is to be used for a solid phase constitutive equation. In addition to the Lame coefficients that are still required as the mechanical properties of the unyielded material, this model also requires a plastic viscosity and a yield stress, viz.
Plastic Viscosity = LINEAR 1.0 2.0
EVP Yield Stress = CONSTANT 50.0
Technical Discussion¶
Detailed theoretical discussion, usage tutorials and troubleshooting tips for this model are covered in the EVP tutorial (GT-019.1). Usage examples for four different strain scenarios are given, including a solid yielding from an applied mechanical load and a solid yielding from high shrinkage stress during drying.
FAQs¶
Problem – Trouble in continuing the first few time steps.
Solution – You may have a fast drying case with slow diffusion in the coating. Instead of decreasing the time step size according to the normal procedure and intuition, increase the time step size. With fast drying and slow diffusion, the initial concentration gradient is very steep at the drying surface. This is a very difficult numerical problem to solve. So when you increase the time step size, in effect, you are relaxing the concentration gradient the program is solving, that will get you past the initial numerical difficulty. However, even if the code can handle such a condition, the concentration and stress profile may appear very wavy. This waviness only reflects the degree of difficulty the code encountered and is not part of the real solution. In this case, refining the mesh towards the drying surface will only increase the waviness of the solution. Drawing from this observation, coarsening the mesh will also get you past this initial numerical difficulty. Although this condition may pose numerical stability problems initially, it does not affect subsequent solution. And most of the time, one is not interested in the solution from the initial time steps.
Problem – Trouble in converging in the plastic region.
Solution – Reduce the time step size because viscoplasticity is in itself a time dependent problem and elasticity in itself is not. Before the material yields, time dependency is induced only through the drying process. The reduction in time step size depends on the value of the plastic viscosity. The lower the viscosity, the small time step should be used. Also, it takes more iterations to converge a time step in the viscoplastic region than the elastic region, so increasing the maximum allowable iterations per time step will help.
Other Cautions: Always set the MASS_FRACTION in the input file to be the same as the Stress Free Solvent Vol Frac in the material file.
The code has been tested for a wide range of initial solvent volume fractions (up to 0.85). When using very high initial solvent volume fractions (approaching 0.85 or beyond), use with caution.
References¶
GT-019.1: Elastoviscoplastic (EVP) Constitutive Model in GOMA: Theory, Testing, and Tutorial, P. R. Schunk, A. Sun, S. Y. Tam (Imation Corp.) and K. S. Chen, January 11, 2001
S.Y. Tam’s thesis: “Stress Effects in Drying Coatings,” Ph.D Dissertation, University of Minnesota, 1997
Convective Lagrangian Velocity¶
Convective Lagrangian Velocity = {model_name} {float_list} [L/t]
Description / Usage¶
In solid mechanics, when the deformation of the mesh is Lagrangian, i.e., motion of the solid can be described by a mapping from the stress-free state (undeformed state) to the deformed state, it is often desirable to prescribe a convective velocity of the stress-free state that can lead to inertial forces through deformation (see Technical Discussion below). This required card allows for the specification of solid-body translation or rotation of the stress-free state, and results in an inertial term on the otherwise quasi static solid momentum equation.
Definitions of the input parameters are as follows:
{model_name} |
Name of the prescribed velocity model. This parameter can have one of the following values: NONE, CONSTANT, or ROTATIONAL. |
{float_list} |
One or more floating point numbers (<float1> through <floatn>) whose values are determined by the selection for {model_name}. These are identified in the discussion of each model below. Note that not all models employ a {float_list}. |
Thus,
NONE |
the stress-free state is assumed to be unmoving. No floating point input values are required with this model. |
CONSTANT <float1> <float2> <float3> |
the stress-free state is one of solid-body translation, viz. it moves uniformly with a velocity specified by three orthogonal components:
|
ROTATIONAL <float1> <float2> <float3> <float4> |
the stress-free state is one of solid-body rotation at a specified rotation rate.
Note that this model is applicable in 2-D and certain 3-D problems in which the rotation axis is the Z-axis. To generalize this model to three-dimensions, the proper input will require a point and a direction of the rotation axis. In two-dimensions, the axis of rotation is the Z-direction. |
Examples¶
The following is a sample input card:
Convective Lagrangian Velocity = ROTATIONAL 25.0 1. 1. 0.
This card is associated with a material file, and hence a material that is of LAGRANGIAN or TOTAL_ALE type (see Mesh Motion card). That material’s stressfree state, as specified by this model, will rotate about an axis that is located at [1.0, 1.0, 0] at 25 radians/sec (assuming seconds are the time scale of the problem).
Technical Discussion¶
This capability is often used when problems require a force or a boundary condition to be applied to a solid material that is moving relative to the source, or the desired frame of reference. Such constraints arise mainly in fluid-structure interaction problems where one solid material is moving relative to another, with a fluid material in between, e.g. deformable blade or knife metering/pushing liquid over a flat or round substrate. These models have also been used in porous-material translation relative to a drying source (see references below).
Specification of any model but NONE on this card produces the left-hand-side term in the equation for quasi static equilibrium:
\(\sigma\) is the Cauchy stress tensor of the solid material, and f is the body force per unit volume. The first term is a result of the specified advection of the stress-free state. \(v_m^0\), which depends solely on the user-prescribed velocity and the current state of deformation, is by definition
where \(F_m\) is the material deformation gradient tensor (computed somewhat differently depending on the formulation, as described in the references below), and \(v_sfs\) is the stress-free state velocity field specified by this card.
References¶
SAND96-2149: Drying in Deformable Partially-Saturated Porous Media: Sol-Gel Coatings, Cairncross, R. A., P. R. Schunk, K. S. Chen, S. S. Prakash, J. Samuel, A. J. Hurd and C. Brinker (September 1996)
GT-005.3: THE NEW TOTAL-ARBITRARY-LAGRANGIAN-EULERIAN (TALE) CAPABILITY and its applicability to coating with/on deformable media, August 6, 1999, P. R. Schunk
SAND2000-0807: TALE: An Arbitrary Lagrangian-Eulerian Approach to Fluid- Structure Interaction Problems, P. R. Schunk (May 2000)
Lame MU¶
Lame MU = {model_name} {float_list} [M/ :math:`Lt^2`]
Description / Usage¶
This required card is used to specify the model for the Lame coefficient μ for the solid constitutive equation (see Sackinger, et. al. 1995, and Solid Constitutive Equation card); this coefficient is equivalent to the shear modulus G in most cases, as described below.
Definitions of the input parameters are as follows:
{model_name} |
Name of the Lame Mu coefficient model. This parameter can have one of the following values: CONSTANT, POWER_LAW, CONTACT_LINE, SHEAR_HARDEN, EXPONENTIAL, DENSE_POWER_LAW, or USER. |
{float_list} |
One or more floating point numbers (<float1> through <floatn>) whose values are determined by the selection for {model_name}. These are identified in the discussion of each model. |
The details of each model option are given below:
CONSTANT <float1> |
For the CONSTANT model, {float_list} is a single value: <float1> - Standard value of the coefficient \(\mu\). (See Technical Discussion.) |
POWER_LAW <float1> <float2> <float3> |
The POWER_LAW model is only to be used for deformable porous media where the shear modulus is allowed to vary as a power of the porosity, \(\phi\) (see Scherer, 1992): The {float_list} contains three values for this model, where: .. figure:: /figures/360_goma_physics.png :align: center :width: 90%
|
CONTACT_LINE <float1> <float2> <float3> <float4> |
The CONTACT_LINE model is a convenient way to control mesh deformation near a fixed point and is normally used ONLY for ARBITRARY Mesh Motion types. This model enables the user to make the shear modulus much larger near the contact line (fixed point) than far away from the contact line, so that elements near the contact line are forced to retain their shape. The shear modulus in this model varies inversely with distance from the contact line: r is the distance from the fixed point, \(r_0\) is a decay length, \(G_0\) is the modulus at the contact line. The {float_list} contains four values for this model, where:
|
SHEAR_HARDEN <float1> <float2> |
The SHEAR_HARDEN model is: where \(\chi\) is the coefficient of variation, \(II_E\) is the second invariant of the strain tensor (see Solid Constitutive Equation card), \(G_0\) is the modulus at zero shear. The {float_list} contains two values for this model, where:
|
EXPONENTIAL <float1> <float2> <float3> |
The EXPONENTIAL model is used exclusively for poroelastic problems, and allows for an exponential dependence of the shear modulus \(\mu\) (or G) on porosity: where \(\lambda\) is the rate of decay, \(\phi_0\) is the porosity in the stress-free state, \(G_0\) is the modulus at zero shear.
|
DENSE_POWER_LAW <float1> <float2> |
The DENSE_POWER_LAW model is used mostly for drying/consolidation problems for which it is desired to have a plateau max-pack modulus behavior. This option requires input from the Stress Free Solvent Vol Frac card (\(y_0\) in equation below), and is used for solvent drying from a condensed, gelled phase. The functional form for the shear modulus is where m is the power law exponent, F is deformation gradient tensor (see Solid Constitutive Equation card), and \(G_0\) is the modulus at zero shear. This function is truncated or clipped at the low end value at G=:math:10^-12.
|
TABLE <integer1> <character_string1> {LINEAR | BILINEAR} [integer2] |
Please see discussion at the beginning of the material properties chapter 5 for input description and options. |
USER <float1>,…, <floatn> |
For the USER model, {float_list} is of arbitrary length, and the values are used through the param[] array in usr_lame_mu function to parameterize a user-defined model. See examples in user_mp.c. |
All modulus values in these equations have the same units as Lame Mu, i.e., M/Lt2.
Technical Discussion¶
Note that \(\mu\) and \(\lambda\), (see the Lame LAMBDA card) are related to the more often used Young’s Modulus and Poisson’s Ratio by the following standard expressions:
where E is the Young’s modulus and υ is Poisson’s ratio. A significant limiting case is approached as \(\nu\) approaches 0.5, in which case the solid becomes incompressible.
The POWER_LAW option could easily be adapted to a concentration measure, viz. made dependent on the concentration of some species (see EQ = species_bulk card). This can be done through the user option, and in fact in usr_lame_mu function of file user_mp.c in the Goma distribution has an example that is appropriate. Also note that all of these models are available for the elastoviscoplastic option on the Plasticity card, and for the real-solid in TOTAL_ALE mesh motion.
FAQs¶
Important note that when one desires an incompressible solid through the use of INCOMP_PSTRAIN type models, by using an incompressible continuity equation in a LAGRANGIAN mesh region (see EQ = continuity), then the bulk modulus, or Lame Lambda expansion term is also added on. So to get a truly incompressible response, one must set the Lame LAMBDA coefficient to zero.
References¶
Sackinger, P. A., Schunk, P. R. and Rao, R. R. 1995. “A Newton-Raphson Pseudo-Solid Domain Mapping Technique for Free and Moving Boundary Problems: A Finite Element Implementation”, J. Comp. Phys., 125 (1996) 83-103.
Scherer, G.W., 1992, “Recent Progress in Drying of Gels”, J. of Non-Crystalline Solids, 147&148, 363-374
GT-001.4: GOMA and SEAMS tutorial for new users, February 18, 2002, P. R. Schunk and D. A. Labreche
GT-019.1: Elastoviscoplastic (EVP) Constitutive Model in GOMA: Theory, Testing, and Tutorial, P. R. Schunk, A. Sun, S. Y. Tam (Imation Corp.) and K. S. Chen, January 11, 2001
GTM-027: Probing Plastic Deformation in Gelatin Films during Drying, M. Lu, S. Y. Tam, A. Sun, P. R. Schunk and C. J. Brinker, 2000
SAND96-2149: Drying in Deformable Partially-Saturated Porous Media: Sol-Gel Coatings, Cairncross, R. A., P. R. Schunk, K. S. Chen, S. S. Prakash, J. Samuel, A. J. Hurd and C. Brinker (September 1996)
Lame LAMBDA¶
Lame LAMBDA = {model_name} {float_list} [M/Lt2]
Description / Usage¶
This required card is used to specify the model for the Lame coefficient λ for the solid constitutive equation (see Sackinger, et. al., 1995). When using a nonlinear constitutive equation for ALE mesh motion, this coefficient is related to the bulk modulus:
Definitions of the input parameters are as follows:
{model_name} |
Name of the Lame LAMBDA model. This parameter can have one of the following values: CONSTANT, POWER_LAW, EXPONENTIAL or USER. |
{float_list} |
One or more floating point numbers (<float1> through <floatn>) whose values are determined by the selection for {model_name}. These are identified in the discussion of each model below. |
The models are described here.
CONSTANT <float1> |
For the CONSTANT model, {float_list} is a single value (see Lame MU card for relationship to other more common elastic constants):
|
POISSON_RATIO <float1> |
For any Lame MU model (see Lame MU card) this option uses the following formula to compute Lame Lame LAMBDA:
|
POWER_LAW <float1> <float2> <float3> |
The POWER_LAW model can be used in deformable porous media where the Lame coefficient varies as a power of the porosity, \(\phi\) (Scherer, 1992): The {float_list} contains three values for this model, where:
|
USER <float1>,…, <floatn> |
For the USER model, {float_list} is of arbitrary length, and the values are used through the param[] array in usr_lame_lambda function to parameterize a userdefined model. See examples in user_mp.c. |
Technical Discussion¶
Please see the Solid Constitutive Equation card for details on the use of this parameter. Special consideration is required for INCOMP* type constitutive equations. The isotropic stress term, or pressure, in that case is added onto the constitutive equation, and so this parameter must be set to zero so as to prevent any compressibility.
Important note that when one desires an incompressible solid through the use of INCOMP_PSTRAIN type models, by using an incompressible continuity equation in a LAGRANGIAN mesh region (see EQ = continuity), then the bulk modulus, or Lame Lambda expansion term is also added on. So to get a truly incompressible response, one must set the Lame LAMBDA coefficient to zero.
References¶
Sackinger, P. A., Schunk, P. R. and Rao, R. R. 1995. “A Newton-Raphson Pseudo-Solid Domain Mapping Technique for Free and Moving Boundary Problems: A Finite Element Implementation”, J. Comp. Phys., 125 (1996) 83-103.
Scherer, G.W., 1992, “Recent Progress in Drying of Gels”, J. of Non-Crystalline Solids, 147&148, 363-374
GT-001.4: GOMA and SEAMS tutorial for new users, February 18, 2002, P. R. Schunk and D. A. Labreche
SAND96-2149: Drying in Deformable Partially-Saturated Porous Media: Sol-Gel Coatings, Cairncross, R. A., P. R. Schunk, K. S. Chen, S. S. Prakash, J. Samuel, A. J. Hurd and C. Brinker (September 1996)
Stress Free Solvent Vol Frac¶
Stress Free Solvent Vol Frac = CONSTANT <float> []
Description / Usage¶
This required card is used to specify the model for the stress-free solvent volume fraction, which is the volume fraction of solvents in the solid material in its stress-free state. This card is used exclusively in materials of LAGRANGIAN or TOTAL_ALE Mesh Motion types (see Mesh Motion card) which are being modeled as gelled solids laden with solvent. At the gel-point, the solid is considered to be stress free, after which a reduction of solvent leads to volume shrinkage and hence a rising stress state. Definitions of the input parameters are as follows:
CONSTANT |
Name of the model for the stress-free solvent volume fraction. |
<float> |
The value of the stress-free solvent volume fraction; this value is unitless. |
Examples¶
The following is a sample card:
Stress Free Solvent Vol Frac = CONSTANT 0.5
This specification sets the volume fraction of solvent in the material to 50 per cent. That volume fraction is tantamount to the gel point of the material.
Technical Discussion¶
The stress free state volume fraction of solvent is basically the solvent fraction at which a material gels, viz., the state at which the material solidifies from a liquid state. This quantity is used in the continuity equation for incompressible solid materials, through which is transported by a variety of diffusion models (see Diffusivity card). The continuity equation, viz., EQ = continuity, is applied as follows:
where the dependent variable is the solid phase pressure (see Solid Constitutive Equation card). Here det F is the determinant of the deformation gradient tensor, yi is the volume fraction of component i (specified by the EQ = species_bulk card), and y0 is the volume fraction of total solvents at the stress free state. Clearly, as the solvent concentration decreases the local volume of solid decreases, creating a rising stress.
References¶
GT-001.4: GOMA and SEAMS tutorial for new users, February 18, 2002, P. R. Schunk and D. A. Labreche
GT-019.1: Elastoviscoplastic (EVP) Constitutive Model in GOMA: Theory, Testing, and Tutorial, P. R. Schunk, A. Sun, S. Y. Tam (Imation Corp.) and K. S. Chen, January 11, 2001
SAND96-2149: Drying in Deformable Partially-Saturated Porous Media: Sol-Gel Coatings, Cairncross, R. A., P. R. Schunk, K. S. Chen, S. S. Prakash, J. Samuel, A. J. Hurd and C. Brinker (September 1996)
Solid Thermal Expansion¶
Solid Thermal Expansion = {CONSTANT | SHRINKAGE} <float> [1/T]
Description / Usage¶
This card is used to specify the model for thermal expansion of solid materials. Definitions of the input parameters are as follows:
CONSTANT |
Name of the model for the thermal expansion coefficient. |
SHRINKAGE |
Model for adding solidification shrinkage stress effects for enthalpy models. Experimental only (1/25/2013). |
<float> |
The value of the thermal expansion coefficient. For the SRINKAGE model this float is not used. |
Technical Discussion¶
When solid materials expand due to temperature changes, the strain field is composed of two components, the strain due to the stress field and the strain due to thermal expansion:
The strain due to thermal expansion is given by
where \(\alpha\) is the linear thermal expansion coefficient \(T_0\) and is the reference temperature (see Solid Reference Temperature card). As a result, the solid constitutive relation contains an extra term:
Note, the linear thermal expansion coefficient is presumed to be independent of strain and the Lame constants are presumed to be independent of temperature. (Model is hardwired right now in GOMA source, PRS 1/23/2013).
In the case of the SHRINKAGE model, an additional term is added on to the deviatoric stress:
References¶
For a discussion of linear thermoelasticity, see (Section 6.2)
Malvern, L. E., 1969, Introduction to the Mechanics of a Continuous Medium, Prentice-Hall
Solid Reference Temperature¶
Solid Reference Temperature = CONSTANT <float> [T]
Description / Usage¶
This card is used to specify the model for the solid reference temperature used in the thermal expansion of solid materials. Definitions of the input parameters are as follows:
CONSTANT |
Name of the model for the reference temperature. |
<float> |
A floating point number that is the value of the solid reference temperature, \(T_{ref}\) . |
Technical Discussion¶
See the Solid Thermal Expansion card for a discussion of the use of this property in the linear thermoelasticity of solids.
References¶
No References.
Plastic Viscosity¶
Plastic Viscosity = {CONSTANT | LINEAR} <float1> [float2] [M/L-t]
Description / Usage¶
This card is used to specify the characteristic viscosity of plastic deformation and is required when the Plasticity Equation card is present. Definitions of the input model options are as follows:
CONSTANT |
Name of the model for a constant plastic viscosity.
|
LINEAR |
LINEAR Name of the model for a linear variation in plastic viscosity; this model requires two floating point values as parameters.
|
Examples¶
Following is a sample card:
Plastic Viscosity = LINEAR 1.0 100.
This specification results in a linear variation of plastic viscosity of the elastoviscoplasticity constitutive equation with concentration of solvent species according to the equation above.
Technical Discussion¶
Using the concentration of solvent species as the independent variable in the LINEAR model, the viscosity y at a certain concentration c is:
where \(V_{sf}\) is the stress-free solvent volume fraction and the solvent volume fraction at solidification, which is set by the Stress Free Solvent Vol Fraction card in the material file. The input parameters for the LINEAR model are the plastic viscosity limits \(y_1\) and \(y_2\). NOTE: this model activates a linear dependence on concentration and hence can only be used for cases in which there is solvent transport.
So for a typical drying/solidification problem, the material file input deck requirements are shown as follows:
Stress Free Solvent Vol Frac = CONSTANT 0.6
Plasticity Equation = EVP_HYPER
Plastic Viscosity = LINEAR 1.0 2.0
EVP Yield Stress = CONSTANT 50.0
Together with these properties one must specify the elastic constants Lame Mu and Lame Lambda.
Theory¶
See Schunk, et. al., 2001 (GT-019.1).
References¶
GT-019.1: Elastoviscoplastic (EVP) Constitutive Model in GOMA: Theory, Testing, and Tutorial, P. R. Schunk, A. Sun, S. Y. Tam (Imation Corp.) and K. S. Chen, January 11, 2001
GTM-020.0: In-Situ Characterization of Stress Development in Gelatin Film During Controlled Drying, M. Lu, S-Y Tam, P. R. Schunk and C. J. Brinker, March 2000.
GTM-027.0: Probing Plastic Deformation in Gelatin Films during Drying, M. Lu, S. Y. Tam, A. Sun, P. R. Schunk and C. J. Brinker, 2000.
S.Y. Tam’s thesis: “Stress Effects in Drying Coatings,” Ph.D Dissertation, University of Minnesota, 1997
EVP Yield Stress¶
EVP Yield Stress = {CONSTANT | LINEAR} <float1> [<float2>] [M/L-t2]
Description / Usage¶
This card is used to specify the characteristic yield stress for Von Mises yield criterion of plastic deformation and is required when the Plasticity Equation card is present. Definitions of the input parameters are as follows:
CONSTANT |
Name of the model for a constant yield stress.
|
LINEAR |
LINEAR Name of the model for a linear variation in plastic viscosity; this model requires two floating point values as parameters.
|
Examples¶
Following is a sample card:
EVP Yield Stress = LINEAR 1.0 100.
This specification results in a linear variation of yield stress of the elastoviscoplasticity constitutive equation with concentration of solvent species according to the equation above.
Technical Discussion¶
Using the concentration of solvent species as the independent variable, the yield stress y at a certain concentration c is:
where \(V_{sf}\) is the stress-free solvent volume fraction and the solvent volume fraction at solidification, which is set by the Stress Free Solvent Vol Fraction card in the material file. The input parameters for the LINEAR model are the plastic viscosity limits \(y_1\) and \(y_2\). NOTE: this model activates a linear dependence on concentration and hence can only be used for cases in which there is solvent transport.
So for a typical drying/solidification problem, the material file input deck requirements are shown as follows:
Stress Free Solvent Vol Frac = CONSTANT 0.6
Plasticity Equation = EVP_HYPER
Plastic Viscosity = LINEAR 1.0 2.0
EVP Yield Stress = CONSTANT 50.0
Together with these properties one must specify the elastic constants Lame Mu and Lame Lambda.
Theory¶
See Schunk, et. al., 2001 reference.
References¶
GT-019.1: Elastoviscoplastic (EVP) Constitutive Model in GOMA: Theory, Testing, and Tutorial, P. R. Schunk, A. Sun, S. Y. Tam (Imation Corp.) and K. S. Chen, January 11, 2001
GTM-020.0: In-Situ Characterization of Stress Development in Gelatin Film During Controlled Drying, M. Lu, S-Y Tam, P. R. Schunk and C. J. Brinker, March 2000.
GTM-027.0: Probing Plastic Deformation in Gelatin Films during Drying, M. Lu, S. Y. Tam, A. Sun, P. R. Schunk and C. J. Brinker, 2000.
S.Y. Tam’s thesis: “Stress Effects in Drying Coatings,” Ph.D Dissertation, University of Minnesota, 1997
Polymer Viscosity¶
Pseudo-Solid Constitutive Equation = {model_name}
Description / Usage¶
This card specifies the constitutive equation used to control mesh motion for arbitrary Lagrangian Eulerian solid mechanics and is required for use with the TOTAL_ALE mesh motion type (see Mesh Motion card). Details are discussed in references provided below.
The single input parameter is the type of model for the constitutive equation:
{model_name} |
The name of the constitutive equation; {model_name} can be one of the following:
The following models are allowed but not recommended.
|
Note again the requirement that the Mesh Motion type for the material in which this constitutive equation applies must be TOTAL_ALE.
Examples¶
Pseudo-Solid Constitutive Equation = NONLINEAR
This card specifies the mesh motion in the ALE solid region is to conform to the nonlinear elastic model, as described on the Solid Constitutive Equation card. This card is required together with Pseudo-Solid Lame Mu and Pseudo-Solid Lame Lambda cards.
Technical Discussion¶
The Pseudo-Solid mesh motion, like the ARBITRARY mesh motion, is governed by the equations of elasticity. These cards, together with the other cards required by the real solid constitutive behavior, are required for ALE solid mechanics. The theory is explained in detail in the provided references. Throughout the boundary condition options, the user will notice an appended _RS. This signifies that the boundary conditions apply to the real-solid elasticity in TOTAL_ALE problems. All other boundary conditions on force and displacement, viz. those without the _RS, are applied to the mesh motion.
References¶
GT-005.3: THE NEW TOTAL-ARBITRARY-LAGRANGIAN-EULERIAN (TALE) CAPABILITY and its applicability to coating with/on deformable media, August 6, 1999, P. R. Schunk
SAND2000-0807: TALE: An Arbitrary Lagrangian-Eulerian Approach to Fluid- Structure Interaction Problems, P. R. Schunk (May 2000)
Sackinger, P. A., Schunk, P. R. and Rao, R. R. 1995. “A Newton-Raphson Pseudo-Solid Domain Mapping Technique for Free and Moving Boundary Problems: A Finite Element Implementation”, J. Comp. Phys., 125 (1996) 83-103.
Pseudo-Solid Lame MU¶
Pseudo-Solid Lame MU = {model_name} {float_list} [M/Lt2]
Description / Usage¶
This card is required only for TOTAL_ALE mesh motion types (see Mesh Motion card) and is used to specify the model for the Lame coefficient \(\mu\) for the mesh motion solid constitutive equation (see Sackinger et al. 1995, and Solid Constitutive Equation card); this coefficient is equivalent to the shear modulus G. The model list here is abbreviated as compared to the Lame MU card as these properties are just used to aid in the elastic mesh motion, independent of the material.
Definitions of the input parameters are as follows:
{model_name} |
Name of the Lame’ Mu coefficient model. This parameter can have one of the following values: CONSTANT or CONTACT_LINE. |
{float_list} |
One or more floating point numbers (<float1> through <floatn>) whose values are determined by the selection for {model_name}. These are identified in the discussion of each model below. |
The details of each model option are:
CONSTANT <float1> |
|
CONTACT_LINE <float1> <float2> <float3> <float4> |
The CONTACT_LINE model is a convenient way to control mesh deformation near a fixed point and is normally used ONLY for TOTAL_ALE or ARBITRARY Mesh Motion types. This model enables the user to make the shear modulus much larger near the contact line (fixed point) than far away from the contact line, so that elements near the contact line are forced to retain their shape. The shear modulus in this model varies inversely with distance from the contact line: This card specifies the mesh motion in the ALE solid region is to conform to the nonlinear elastic model, as described on the Solid Constitutive Equation card. This card is required together with Pseudo-Solid Lame Mu and Pseudo-Solid Lame Lambda cards. r is the distance from the fixed point, \(r_0\) is a decay length, \(G_0\) is the modulus far from the contact line, and \(G_0\) is the modulus at the contact line. The {float_list} contains four values for this model, where:
|
Examples¶
Pseudo-Solid Lame MU = CONSTANT 0.5
This card specifies that the current material have a constant shear modulus of 0.5 for the mesh elasticity. Note that the real-solid mesh Lame MU is set with the Lame MU card.
Technical Discussion¶
It is best to consult the TALE tutorial (Schunk, 1999) for details of this card.
References¶
GT-005.3: THE NEW TOTAL-ARBITRARY-LAGRANGIAN-EULERIAN (TALE) CAPABILITY and its applicability to coating with/on deformable media, August 6, 1999, P. R. Schunk
Sackinger, P. A., Schunk, P. R. and Rao, R. R. 1995. “A Newton-Raphson Pseudo-Solid Domain Mapping Technique for Free and Moving Boundary Problems: A Finite Element Implementation”, J. Comp. Phys., 125 (1996) 83-103.
Pseudo-Solid Lame LAMBDA¶
Pseudo-Solid Lame LAMBDA = CONSTANT <float> [M/Lt2]
Description / Usage¶
This card is required only for TOTAL_ALE mesh motion types (see Mesh Motion card) and is used to specify the model for the Lame coefficient \(\lambda\) for the mesh motion elasticity (see Sackinger et al., 1995).
This material parameter currently has only one possible model type (CONSTANT) with only a single required input value, as follows:
CONSTANT |
|
Examples¶
The following is a sample input card:
Pseudo-Solid Lame LAMBDA = CONSTANT 1.
This card specifies that the current material have a constant shear modulus of 0.5 for the mesh elasticity. Note that the real-solid mesh Lame MU is set with the Lame MU card.
Technical Discussion¶
See discussion on Lame LAMBDA card and Solid Constitutive Equation card for more details. The main difference here is that this modulus is applied only to the moving mesh, and not the real solid as in an ALE solid mechanics simulation.
References¶
GT-005.3: THE NEW TOTAL-ARBITRARY-LAGRANGIAN-EULERIAN (TALE) CAPABILITY and its applicability to coating with/on deformable media, August 6, 1999, P. R. Schunk
Sackinger, P. A., Schunk, P. R. and Rao, R. R. 1995. “A Newton-Raphson Pseudo-Solid Domain Mapping Technique for Free and Moving Boundary Problems: A Finite Element Implementation”, J. Comp. Phys., 125 (1996) 83-103.
Liquid Constitutive Equation¶
Liquid Constitutive Equation = {model_name}
Description / Usage¶
This required card is used to specify the stress, strain-rate/strain constitutive equation associated with the momentum equations (e.g. Navier-Stokes equations) and contains Newtonian and generalized Newtonian models. The single input parameter is the {model_name} with the options listed below:
- {model_name}
Name of the constitutive equation, being one of the following values: NEWTONIAN, POWER_LAW, CARREAU, BINGHAM, CARREAU_WLF, CURE, THERMAL, EPOXY, SUSPENSION, FILLED_EPOXY, POWERLAW_SUSPENSION, CARREAU_SUSPENSION, or HERSCHEL_BULKLEY. Each of these constitutive models require additional parameters that are entered via additional cards, as described below.
Thus,
- NEWTONIAN
For a simple constant viscosity Newtonian fluid. This model requires one floating point value,
\(\mu\), where \(\mu\) is the viscosity in the chosen units for the problem and is entered with the Viscosity card.
- POWER_LAW
For a power law model. This model requires two parameters. The first, μ0, is the zero strain-rate limit of the viscosity and is entered with the Low Rate Viscosity card. The second, n, is the exponent on the strain rate which can take on any value between 1 (Newtonian) and 0 (infinitely shear thinning). n is entered with the Power Law Exponent card. The form of the equation is
where is the second invariant of the shear-rate tensor. To obtain solutions with the power law model, it is best to start with a Newtonian initial guess since the viscosity becomes infinite at zero shear-rate.
- CARREAU
For a Carreau-Yasuda strain-rate thinning or thickening relation. This option requires five floating point values. The first, μ0, is the zero strain-rate limit of the viscosity and is entered with the Low Rate Viscosity card. The second, n, is the exponent on the strain rate which can take on any value between 1 (Newtonian) and 0 (infinitely shear thinning). n is entered with the Power Law Exponent card. The third, μinf, is the high-strainrate limit to the viscosity and is entered with the High Rate Viscosity card. The fourth, λ, is the time constant reflecting the strain-rate at which the transition between μ0 and μinf takes place. λ is entered with the Time Constant card. The fifth, a, is a dimensionless parameter that describes the transition between the low-rate and the power-law region and is entered with the Aexp card. The form of the equation is
where is the second invariant of the shear-rate tensor.
- BINGHAM
For a Bingham-Carreau-Yasuda fluid. This option requires eight floating point values. It uses the same parameters as the CARREAU model with the addition of coefficients to describe the yield and temperature dependent behavior. The first, μ0, is the zero strain-rate limit of the viscosity and is entered with the Low Rate Viscosity card. The second, n, is the exponent on the strain rate which can take on any value between 1 (Newtonian) and 0 (infinitely shear thinning). n is entered with the Power Law Exponent card. The third, μinf, is the high-strain-rate limit to the viscosity and is entered with the High Rate Viscosity card. The fourth, λ, is the time constant reflecting the strain-rate at which the transition between μ0 and μinf takes place. λ is entered with the Time Constant card. The fifth, a, is a dimensionless parameter that describes the transition between the low-rate and the power-law region and is entered with the Aexp card. The form of the equation is
where is a simplified temperature dependent shift factor that is expressed as an Arrhenius type temperature dependence of the following form:
The exponent for the temperature dependence, Eμ/R, is input using the Thermal Exponent card. Tref is input using the Reference Temperature card in the thermal properties section of the material file. The stress at which the material yields is input with the Yield Stress card. The sharpness of the transition from the solid to fluid state, F, is indicated with the Yield Exponent card.
- CARREAU_WLF
An extension of the Carreau-Yasuda model to incorporate a temperature-dependent shift in shear-rate according to the Williams-Landel-Ferry equation (Hudson and Jones, 1993). The form of the equation is
where \(a_T\) is another form of the temperature-dependent shift factor:
Here is a thermal exponential factor (can be Arrhenius) and is input by the Thermal Exponent card; \(c_2\) is the WLF constant 2 and is input by the Thermal WLF Constant2 card. μ0, is the zero strain-rate limit of the viscosity and is entered with the Low Rate Viscosity card. n, is the exponent on the strain rate which can take on any value between 1 (Newtonian) and 0 (infinitely shear thinning) and is entered with the Power Law Exponent card. \(μ_{inf}\), is the high-strain-rate limit to the viscosity and is entered with the High Rate Viscosity card. λ, is the time constant reflecting the strain-rate at which the transition between μ0 and μinf takes place and is entered with the Time Constant card. a, is a dimensionless parameter that describes the transition between the low-rate and the power-law region and is entered with the Aexp card.
- CURE
For a model to increase the viscosity with the extent of reaction. The Cure model can be used to represent polymerizing systems whose viscosity depends on the extent of reaction. The form of the equation is
This option requires four floating point values. The first, μ0, is the reference state viscosity and is entered with the Low Rate Viscosity card. The constant, \(α_g\), is entered with the Cure Gel Point card and marks the extent of reaction at the transition from the liquid to the solid state. The exponents A and B are entered with the Cure A Exponent and Cure B Exponent cards.
- THERMAL
For a temperature-dependent viscosity. This option, which requires two floating point values, can be used to represent fluids that change viscosity with temperature. The form of the equation is
where the reference state viscosity, μ0, is entered with the Low Rate Viscosity card. The exponent, Eμ/R, is specified using the Thermal Exponent card.
- EPOXY
For a thermal and curing component. The Epoxy model combines the temperature dependence of the THERMAL option with the extent of reaction dependence of the CURE option. The functional form of the equation is:
Five cards must be used to specify all the parameters for this model. The first, μ0, is the reference state viscosity and is entered with the Low Rate Viscosity card. The thermal exponent, Eμ/R, is specified using the Thermal Exponent card. The constant, \(α_g\), is entered with the Cure Gel Point card and marks the extent of reaction at the transition from the liquid to the solid state. The exponents A and B are entered with the Cure A Exponent and Cure B Exponent cards.
- SUSPENSION
For simulating a carrier fluid with high-volume fraction particles. This option invokes a concentrationdependent viscosity model useful in modeling solid suspensions. The functional form associated with this option is,
where μ0 is effectively the viscosity of the suspending fluid specified with the Low Rate Viscosity card, n is an exponent specified by the Power Law Exponent card and is typically less than zero. \(C_{max}\) is the “binding” solid concentration and is specified with the Suspension Maximum Packing card. Ci is the solid concentration and is tied to a convective-diffusion equation specified in the equation section of the Problem Description. The correct species number “i” is specified with the Suspension Species Number card. Note that for \(C_i\) > \(C_{max}\) and n < 0, the model as written above is physically undefined. For concentrations in this range, a very large value for viscosity will be used, effectively solidifying the material.
- FILLED_EPOXY
This option combines the cure and thermal dependence of the EPOXY model with the solid volume fraction dependence of the SUSPENSION model. The functional form of this equation is
with the temperature \(T_g\) being calculated from
Here the viscosity now depends on extent of reaction, temperature and solid volume fraction. Nine cards must be specified to define the parameters for this option and are entered in the following manner. The first, μ0, is the reference state viscosity and is entered with the Low Rate Viscosity card. n is the exponent for suspension behavior and is specified by the Power Law Exponent card; it is typically less than zero. \(C_{max}\) is the “binding” solid concentration and is specified with the Suspension Maximum Packing card. \(C_i\) is the solid concentration and is tied to a convective-diffusion equation specified in the equation section of the previous chapter. The correct species number “i” is identified with the Suspension Species Number card. Here \(c_1\) is a thermal exponential factor and is input by the Thermal Exponent card; \(c_2\) is a second thermal exponent and is entered via the Cure B Exponent card. The constant for the curing model, \(α_g\), is entered with the Cure Gel Point card and marks the extent of reaction at the transition from the liquid to the solid state. The cure exponent used in the EPOXY model is here assumed to be constant (-4/3) and is fixed in the model. The constant A in the gel temperature equation is entered with the Cure A Exponent card and the temperature is entered with the Unreacted Gel Temperature card. Although it does not appear directly in the model equations, the Cure Species Number must also be specified.
- POWERLAW_SUSPENSION
This is a specialized research model that incorporates the power law model with the suspension model to try and simulate particles suspending in shear-thinning fluid. This option requires five input values. The first, μ0, is the zero strain-rate limit of the viscosity of the solvent and is entered with the Low Rate Viscosity card. The second, n, is the exponent on the strain rate which can take on any value between 1 (Newtonian) and 0 (infinitely shear thinning). n is entered with the Power Law Exponent card. The third value is the exponent for the suspension Krieger model, which is input through the Thermal Exponent, m. The fourth term is the suspension maximum packing, \(C_{max}\), which is entered through the Suspension Maximum Packing card. \(C_i\) is the solid concentration and is tied to a convectivediffusion equation specified in the equation section of the previous chapter. The correct species number “i” is identified with the Suspension Species Number card. The form of the equation is
where y is the second invariant of the shear-rate tensor. It is best to start with a Newtonian initial guess for the power law suspension model, since the viscosity for the power law model will become infinite at zero shear-rate.
- CARREAU_SUSPENSION
This model is a hybrid for the flow of particle-laden suspensions in shear-thinning fluids. It uses a Carreau-Yasuda strain-rate thinning or thickening relation for the suspending fluid and a Krieger model for the suspension. This option requires eight input values. The first, μ0, is the zero strain- rate limit of the viscosity and is entered with the Low Rate Viscosity card. The second, n, is the exponent on the strain rate which can take on any value between 1 (Newtonian) and 0 (infinitely shear thinning). n is entered with the Power Law Exponent card. The third, μinf, is the high-strain-rate limit to the viscosity and is entered with the High Rate Viscosity card. The fourth, λ, is the time constant reflecting the strain-rate at which the transition between μ0 and μinf takes place. λ is entered with the Time Constant card. The fifth, a, is a dimensionless parameter that describes the transition between the low-rate and the power-law region and is entered with the Aexp card. The sixth value is the exponent for the suspension Krieger model, which is input through the Thermal Exponent, m. The seventh term is the suspension maximum packing, Cmax, which is entered through the Suspension Maximum Packing card. Ci is the solid concentration and is tied to a convective-diffusion equation specified in the equation section of the previous chapter. The correct species number “i” is identified with the Suspension Species Number card.The form of the equation is
where y is the second invariant of the shear-rate tensor.
- HERSCHEL_BULKLEY
This is a variant on the power law model that includes a yield stress. It requires three input values to operate: a reference viscosity value, μ0, a power-law exponent, n. and a yield shear stress value, \(τ_y\). The model for this constitutive relations is as follows:
The nature of this relation is best seen by multiplying the entire relation by the shear rate to produce a relation between shear stress and shear rate. In this manner it can be seen that the shear stress does not go to zero for zero shear rate. Instead it approaches the yield shear stress value. Put another way, only for imposed shear stresses greater than the yield stress will the fluid exhibit a nonzero shear rate. This is effective yielding behavior.
A caveat needs stating at this point. This model is essentially a superposition of two power-law models. One with the supplied exponent and the other with an implicit exponent of n = 0. It has long been observed that power-law models with exponents approaching zero exhibit very poor convergence properties. The Herschel_Bulkley model is no exception. To alleviate these convergence problems somewhat, the sensitivities of the yield stress term with respect to shear rate has not been included in the Jacobian entries for this viscosity model. This helps in that it allows for convergence at most yield stress values, but also means that the iteration scheme no longer uses an exact Jacobian. The difference is seen in that this model will take relatively more iterations to converge to an answer. The user should expect this and not be too troubled (it’s alright to be troubled a little).
Examples¶
The following is a sample card setting the liquid constitutive equation type to NEWTONIAN and demonstrates the required cards:
Liquid Constitutive Equation = NEWTONIAN
Viscosity = CONSTANT 1.00
The following is a sample card setting the liquid constitutive equation type to POWER_LAW and demonstrates the required cards:
Liquid Constitutive Equation = POWER_LAW
Low Rate Viscosity= CONSTANT 1.
Power Law Exponent= CONSTANT 1.
The following is a sample card setting the liquid constitutive equation type to CARREAU and demonstrates the required cards:
Liquid Constitutive Equation = CARREAU
Low Rate Viscosity= CONSTANT 1.
Power Law Exponent= CONSTANT 1.
High Rate Viscosity= CONSTANT 0.001
Time Constant = CONSTANT 1.
Aexp = CONSTANT 1.
The following is a sample card setting the liquid constitutive equation type to BINGHAM and demonstrates the required cards:
Liquid Constitutive Equation = BINGHAM
Low Rate Viscosity= CONSTANT 10.00
Power Law Exponent= CONSTANT .70
High Rate Viscosity= CONSTANT 0.01
Time Constant = CONSTANT 100.
Aexp = CONSTANT 2.5
Thermal Exponent = CONSTANT 1.
Yield Stress = CONSTANT 5.
Yield Exponent = CONSTANT 1.0
Reference Temperature= CONSTANT 273.
The following is a sample card setting the liquid constitutive equation type to CARREAU_WLF and demonstrates the required cards:
Liquid Constitutive Equation = CARREAU_WLF
Low Rate Viscosity= CONSTANT 10.00
Power Law Exponent= CONSTANT .70
High Rate Viscosity= CONSTANT 0.01
Time Constant = CONSTANT 100.
Aexp = CONSTANT 2.5
Thermal Exponent = CONSTANT 1.
Thermal WLF Constant2 = CONSTANT 0.5
Reference Temperature= CONSTANT 273.
The following is a sample card setting the liquid constitutive equation type to CURE and demonstrates the required cards:
Liquid Constitutive Equation = CURE
Low Rate Viscosity= CONSTANT 1.
Power Law Exponent= CONSTANT 1.
The following is a sample card setting the liquid constitutive equation type to THERMAL and demonstrates the required cards:
Liquid Constitutive Equation = THERMAL
Low Rate Viscosity= CONSTANT 1.
Thermal Exponent= CONSTANT 9.
The following is a sample card setting the liquid constitutive equation type to EPOXY and demonstrates the required cards:
Liquid Constitutive Equation = EPOXY
Liquid Constitutive Equation = FILLED_EPOXY
Low Rate Viscosity= CONSTANT 1.e5
Thermal Exponent= CONSTANT 9.
Cure Gel Point = CONSTANT 0.8
Cure A Exponent= CONSTANT 0.3
Cure B Exponent= CONSTANT 43.8
The following is a sample card setting the liquid constitutive equation type to SUSPENSION and demonstrates the required cards:
Liquid Constitutive Equation = SUSPENSION
Low Rate Viscosity= CONSTANT 1.e5
Power Law Exponent = CONSTANT -3.0
Suspension Maximum Packing= CONSTANT 0.49
Suspension Species Number = 0
The following is a sample card setting the liquid constitutive equation type to FILLED_EPOXY and demonstrates the required cards:
Liquid Constitutive Equation = FILLED_EPOXY
Low Rate Viscosity = CONSTANT 1.e5
Power Law Exponent = CONSTANT -3.0
Thermal Exponent = CONSTANT 9.
Suspension Maximum Packing = CONSTANT 0.49
Suspension Species Number = 0
Cure Gel Point = CONSTANT 0.8
Cure A Exponent = CONSTANT 0.3
Cure B Exponent = CONSTANT 43.8
Cure Species Number = 2
Unreacted Gel Temperature = CONSTANT 243
The following is a sample card setting the liquid constitutive equation type to POWERLAW_SUSPENSION and demonstrates the required cards:
Liquid Constitutive Equation = POWERLAW_SUSPENSION
Low Rate Viscosity= CONSTANT 1.
Power Law Exponent= CONSTANT 1.
Thermal Exponent = CONSTANT -1.82
Suspension Maximum Packing= CONSTANT 0.68
Suspension Species Number= 0
The following is a sample card setting the liquid constitutive equation type to CARREAU_SUSPENSION and demonstrates the required cards:
Liquid Constitutive Equation = CARREAU_SUSPENSION
Low Rate Viscosity= CONSTANT 1.
Power Law Exponent= CONSTANT 1.
High Rate Viscosity= CONSTANT 0.001
High Rate Viscosity= CONSTANT 0.001
Time Constant = CONSTANT 1.
Aexp = CONSTANT 1.
Thermal Exponent = CONSTANT -1.82
Suspension Maximum Packing= CONSTANT 0.68
Suspension Species Number= 0
The following card gives an example of the HERSCHEL_BULKLEY model
Liquid Constitutive Equation = HERSCHEL_BULKLEY
Low Rate Viscosity = CONSTANT 0.337
Power Law Exponent = CONSTANT 0.817
Yield Stress = CONSTANT 1.39
Technical Discussion¶
See Description/Usage section for this card.
Theory¶
The NEWTONIAN, POWER_LAW, and CARREAU models are described in detail in Bird, et al. (1987). Details of the continuous yield stress model used in the Bingham- Carreau-Yasuda (BINGHAM) model, which is a Carreau model combined with a continuous yield stress model, can be found in Papanastasiou (1987).
References¶
Bird, R. B., Armstrong, R. C., and Hassager, O. 1987. Dynamics of Polymeric Liquids, 2nd ed., Wiley, New York, Vol. 1.
Hudson, N. E. and Jones, T. E. R., 1993. “The A1 project - an overview”, Journal of Non-Newtonian Fluid Mechanics, 46, 69-88.
Papanastasiou, T. C., 1987. “Flows of Materials with Yield,” Journal of Rheology, 31 (5), 385-404.
Papananstasiou, T. C., and Boudouvis, A. G., 1997. “Flows of Viscoplastic Materials: Models and Computation,” Computers & Structures, Vol 64, No 1-4, pp 677-694.
Viscosity¶
Viscosity = {model_name} {float_list} [M/Lt]
Description / Usage¶
This card is used to specify the viscosity model for the liquid constitutive equation (see Sackinger et al., 1995). Definitions of the input parameters are as follows:
{model_name} |
The name of the viscosity model, which can be one of the following: CONSTANT, USER, USER_GEN, or FILL, LEVEL_SET, CONST_PHASE_FUNCTION. |
{float_list}. |
One or more floating point numbers (<float1> through <floatn>) whose values are determined by the selection for {model_name}. These are identified in the discussion of each model below. Note that not all models employ a {float_list}. |
Thus,
CONSTANT <float1> |
This option specifies a constant viscosity for a Newtonian fluid. The {float_list} has a single value:
|
USER <float1>… <floatn |
This option specifies that the viscosity will be given by a user-defined model; the model must be incorporated into Goma by modifying function “usr_viscosity” in file user_mp.c. The model parameters are entered in the {float_list} as <float1> through <floatn> and passed to the routine as an array. |
USER_GEN <float1>… <floatn> |
This option specifies that the viscosity will be given by a generalized user-defined model. This user-defined model must be incorporated by modifying the routine “usr_viscosity_gen” in the file user_mp_gen.c. Any number of parameters can be passed (via <float1> through <floatn>) in here. |
FILL <float1> <float2> |
The {float_list} for this option requires two values. It invokes a FILL dependent viscosity that is set to the value of float1 if the FILL variable is 1 and float2 if the FILL variable is 0. |
LEVEL_SET <float1> <float2> <float3> |
This model is used to vary the viscosity in the flow region when a level set function is used to track the boundary between two fluids using level set interface tracking. This choice assures a smooth transition in density across the zero level set contour. The {float_list} contains three values for this model, where:
Note: a better way to specify the identical viscosity model is to make use of the 2nd Level Set Viscosity card documented also in this manual. |
CONST_PHASE_FUNCTION <floatlist> <float1> <float2> |
This model is used to vary the viscosity in the flow regime when phase functions are used to track the motion of muliple phases. This choice assures a smooth transition in viscosity across the phase boundaries. The {float_list} contains a variable number of values that depend on the number phase functions being tracked, where:
The user should examine the CONST_PHASE_FUNCTION density model for a detailed description of the relations used to compute viscosity with this model. That model refers to densities but the same equations apply if viscosities are exchanged for densities. |
TABLE <integer1> <character_string1> {LINEAR | BILINEAR} [integer2] [FILE = filenm] |
Please see discussion at the beginning of the material properties chapter 5 for input description and options. Currently the only valid options for character_string1 is TEMPERATURE and MASS_FRACTION. |
Examples¶
The following is a sample card that sets the viscosity to USER:
Viscosity = USER 1. 1. 1. 1. 1.
Viscosity = LEVEL_SET 0.083 0.0001 0.1
Technical Discussion¶
The viscosity specified by this input card is used with the NEWTONIAN Liquid Constitutive Equation.
References¶
Sackinger, P. A., Schunk, P. R. and Rao, R. R. 1995. “A Newton-Raphson Pseudo-Solid Domain Mapping Technique for Free and Moving Boundary Problems: A Finite Element Implementation”, J. Comp. Phys., 125 (1996) 83-103.
Low Rate Viscosity¶
Low Rate Viscosity = CONSTANT <float> [M/Lt]
Description / Usage¶
This card is used to specify the model for the low-rate viscosity parameter for the POWER_LAW, CARREAU, CARREAU_WLF, BINGHAM, SUSPENSION, THERMAL, CURE, EPOXY, FILLED_EPOXY, POWERLAW_SUSPENSION and CARREAU_SUSPENSION model options of the Liquid Constitutive Equation card. This is also the reference viscosity value in the HERSCHEL_BULKLEY constitutive equation.
Definitions of the input parameters are as follows:
CONSTANT |
Name of the model for the low-rate viscosity.
|
LEVEL_SET |
Name of the model for level-set dependent low-rate viscosity. Allows for this viscosity level to be a function of the level-set field. Specifically used for changing the low-rate viscosity from one constant value on the negative side of the interface to another constant value on the positive side. The model requires three floats:
|
Examples¶
The following is a sample card that sets the low rate viscosity to 10:
Low Rate Viscosity = CONSTANT 10.
Technical Discussion¶
See Description/Usage for Liquid Constitutive Equation card.
References¶
No References.
Power Law Exponent¶
Power Law Exponent = CONSTANT <float> []
Description / Usage¶
This card is used to specify the model for the power-law exponent parameter of the POWER_LAW, CARREAU, BINGHAM, CARREAU_WLF, CURE, SUSPENSION, FILLED_EPOXY, POWERLAW_SUSPENSION, CARREAU_SUSPENSION, and HERSCHEL_BULKLEY fluid options of the Liquid Constitutive Equation card.
Definitions of the input parameters are as follows:
CONSTANT |
Name of the model for the power-law exponent.
|
LEVEL_SET |
Name of the model for level-set dependent power law exponent. Specifically used for changing the exponent from one constant value on the negative side of the interface to another constant value on the positive side. The model requires three floats:
|
Examples¶
The following is a sample card that sets the power law exponent to 0.2:
Power Law Exponent = CONSTANT 0.2
Technical Discussion¶
See Description/Usage for Liquid Constitutive Equation card.
References¶
No References.
High Rate Viscosity¶
High Rate Viscosity = CONSTANT <float> [M/Lt]
Description / Usage¶
This card is used to specify the model for the high-rate viscosity parameter of the CARREAU, BINGHAM, CARREAU_WLF and CARREAU_SUSPENSION fluid options of the Liquid Constitutive Equation card. Definitions of the input parameters are as follows:
CONSTANT |
Name of the model for the high-rate viscosity.
|
LEVEL_SET |
Name of the model for level-set dependent high-rate viscosity. Allows for this viscosity level to be a function of the level-set field. Specifically used for changing the high-rate viscosity from one constant value on the negative side of the interface to another constant value on the positive side. The model requires three floats:
|
Examples¶
The following is a sample card that sets the high rate viscosity to 10.:
High Rate Viscosity = CONSTANT 10.
Technical Discussion¶
See Description/Usage for Liquid Constitutive Equation card.
References¶
No References.
Time Constant¶
Time Constant = CONSTANT <float> [t]
Description / Usage¶
This card is used to specify the model for the time constant parameter of the CARREAU, BINGHAM, CARREAU_WLF and CARREAU_SUSPENSION fluid options of the Liquid Constitutive Equation card. Definitions of the input parameters are as follows:
CONSTANT |
Name of the model for the time constant.
|
LEVEL_SET |
Name of the model for level-set dependent time constant. Allows for this time constant level to be a function of the level-set field. Specifically used for changing the time constant from one constant value on the negative side of the interface to another constant value on the positive side. The model requires three floats:
|
Examples¶
The following is a sample card that sets the time constant to 0.2.
Time Constant = CONSTANT 0.2
Technical Discussion¶
See Description/Usage for Liquid Constitutive Equation card.
Aexp¶
Aexp = CONSTANT <float> []
Description / Usage¶
This card is used to specify the model for the Aexp parameter of the CARREAU,BINGHAM, CARREAU_WLF and CARREAU_SUSPENSION model options of the Liquid Constitutive Equation card. Definitions of the input parameters are as follows:
CONSTANT |
Name of the model for Aexp.
|
LEVEL_SET |
Name of the model for level-set dependent Aexp parameter. Allows for this parameter level to be a function of the level-set field. Specifically used for changing the Aexp parameter from one constant value on the negative side of the interface to another constant value on the positive side. The model requires three floats:
|
Technical Discussion¶
See Description/Usage for Liquid Constitutive Equation card.
References¶
Bird, R. B., Armstrong, R. C., and Hassager, O. 1987. Dynamics of Polymeric Liquids, 2nd ed., Wiley, New York, Vol. 1.
Thermal Exponent¶
Thermal Exponent = CONSTANT <float> [T]
Description / Usage¶
This card is used to specify a thermal exponential factor for CARREAU_WLF, BINGHAM, THERMAL, EPOXY, FILLED_EPOXY, POWERLAW_SUSPENSION and CARREAU_SUSPENSION viscosity models, as selected in the Liquid Constitutive Equation card. The value represented by the thermal exponent varies between these liquid constitutive models; the appropriate values for each model is indicated below.
Definitions of the input parameters are as follows:
CONSTANT |
Name of the model for the thermal exponent.
|
LEVEL_SET |
Name of the model for level-set dependent thermal exponent factor. Allows for this exponent level to be a function of the level-set field. Specifically used for changing the thermal exponent from one constant value on the negative side of the interface to another constant value on the positive side. The model requires three floats:
|
Examples¶
The following is a sample card that sets the thermal exponent to 0.5.
Thermal Exponent = CONSTANT 0.5
Technical Discussion¶
See Description/Usage for Liquid Constitutive Equation card.
Thermal WLF Constant2¶
Thermal WLF Constant2 = CONSTANT <float> [T]
Description / Usage¶
This card is used to specify the thermal constant 2 of the CARREAU_WLF viscosity model in the Liquid Constitutive Equation card. Definitions of the input parameters are as follows:
CONSTANT |
Name of the model for Thermal Constant2.
|
LEVEL_SET |
Name of the model for level-set dependent WLF thermal constant 2. Allows for this thermal constant 2 level to be a function of the level-set field. Specifically used for changing the thermal constant 2 from one constant value on the negative side of the interface to another constant value on the positive side. The model requires three floats:
|
Examples¶
The following is a sample card that sets the Thermal WLF Constant2 to 0.1.
Thermal WLF Constant2 = CONSTANT 0.1
Technical Discussion¶
See Description/Usage for Liquid Constitutive Equation card.
Yield Stress¶
Yield Stress = CONSTANT <float> [M/Lt2]
Description / Usage¶
This card is used to specify the model for the yield stress parameter, \(τ_y\), of the BINGHAM and HERSCHEL_BULKLEY model options of the Liquid Constitutive Equation card. Definitions of the input parameters are as follows:
CONSTANT |
Name of the model for the yield stress.
|
Examples¶
The following is a sample card that sets the yield stress to 100:
Yield Stress = CONSTANT 100.
Technical Discussion¶
See Description/Usage for Liquid Constitutive Equation card.
Yield Exponent¶
Yield Exponent = CONSTANT <float> [t]
Description / Usage¶
This card is used to specify the model for the yield exponent parameter, F, for the BINGHAM model option of the Liquid Constitutive Equation card, or when the Polymer Constitutive Equation card is SARAMITO_OLDROYDB, SARAMITO_GIESEKUS, or SARAMITO_PTT. Definitions of the input parameters are as follows:
- CONSTANT <float>
Name of the model for the yield exponent. <float> the value of the yield exponent, F, which has the dimensions of inverse shear-rate in whatever units are consistent with the problem of interest and which connotes the steepness of the transition from solid to fluid behavior for the Bingham-Carreau-Yasuda model or the Saramito yield stress model.
For the BINGHAM model, if F is large, the material has an abrupt transition from solid-like to fluid-like behavior, whereas for a small F, the transition is more gradual.
For the SARAMITO_OLDROYDB, SARAMITO_GIESEKUS, and SARAMITO_PTT models, the material has and abrupt transition when F equals zero. This Transistion becomes smooth for nonzero when F is greater than zero, with the transition becoming more gradual as F increases.
Examples¶
The following is a sample card that sets the yield exponent to 10.0
Yield Exponent = CONSTANT 10.0.
Technical Discussion¶
See Description/Usage for Liquid Constitutive Equation and Polymer Constitutive Equation cards.
Suspension Maximum Packing¶
Suspension Maximum Packing = CONSTANT <float> []
Description / Usage¶
This card is used to specify the model for the \(C{max}\) parameter of the SUSPENSION and FILLED_EPOXY model options of the Liquid Constitutive Equation card. Definitions of the input parameters are as follows:
CONSTANT |
Name of the model for suspension maximum packing.
|
Examples¶
The following is a sample card that sets the suspension maximum packing:
Suspension Maximum Packing = CONSTANT 0.68.
Technical Discussion¶
See Description/Usage for Liquid Constitutive Equation card.
Suspension Species Number¶
Suspension Species Number = <integer>
Description / Usage¶
This card is used to specify the value of the species number “i” of the SUSPENSION and FILLED_EPOXY model options of the Liquid Constitutive Equation card. Definitions of the input parameters are as follows:
<integer> - the species number “i”.
Examples¶
The following is a sample card that sets the suspension species number to 1:
Suspension Species Number = 1
Technical Discussion¶
See Description/Usage for Liquid Constitutive Equation card.
Cure Gel Point¶
Cure Gel Point = CONSTANT <float> []
Description / Usage¶
This card is used to specify the model for the \(α_g\) parameter for the CURE, EPOXY, and FILLED_EPOXY model options of the Liquid Constitutive Equation card. Definitions of the input parameters are as follows:
CONSTANT |
Name of the model for the \(α_g\) parameter.
|
Examples¶
The following is a sample card that sets the cure gel point to 0.75:
Cure Gel Point = CONSTANT 0.75
Technical Discussion¶
See Description/Usage for Liquid Constitutive Equation card.
Cure A Exponent¶
Cure A Exponent = CONSTANT <float> []
Description / Usage¶
This card is used to specify the model for the A exponent of the CURE, EPOXY, and FILLED_EPOXY model options of the Liquid Constitutive Equation card. Definitions of the input parameters are as follows:
CONSTANT |
Name of the model for the A exponent.
|
Examples¶
The following is a sample card that sets the cure A exponent to 1.0:
Cure A Exponent = CONSTANT 1.0
Technical Discussion¶
See Description/Usage for Liquid Constitutive Equation card.
Cure B Exponent¶
Cure B Exponent = CONSTANT <float> []
Description / Usage¶
This card is used to specify the model for the B exponent of the CURE, EPOXY, and FILLED_EPOXY model options of the Liquid Constitutive Equation card. Definitions of the input parameters are as follows:
CONSTANT |
Name of the model for the B exponent.
|
Examples¶
The following is a sample card that sets the cure B exponent to 0.1:
Cure B Exponent = CONSTANT 0.1.
Technical Discussion¶
See Description/Usage for Liquid Constitutive Equation card.
Cure Species Number¶
Cure Species Number = <integer>
Description / Usage¶
This card is used to specify the species number, e.g., the i in \(C_i\), for the FILLED_EPOXY model options of the Liquid Constitutive Equation card. Definitions of the input parameters are as follows:
<integer> - the value of the species equation, i, associated with tracking the curing species.
Examples¶
The following is a sample card that sets the cure species number to 0.
Cure Species Number = 0
Technical Discussion¶
See Description/Usage for Liquid Constitutive Equation card.
Unreacted Gel Temperature¶
Unreacted Gel Temperature = CONSTANT <float>
Description / Usage¶
This card is used to specify the model for the unreacted gel temperature parameter for the FILLED_EPOXY fluid option of the Liquid Constitutive Equation card.
Definitions of the input parameters are as follows:
CONSTANT |
Name of the model for the unreacted gel temperature.
|
Examples¶
The following is a sample card that sets the unreacted gel temperature to 273.0:
Power Law Exponent = CONSTANT 273.0
Technical Discussion¶
See Description/Usage for Liquid Constitutive Equation card.
Polymer Constitutive Equation¶
Polymer Constitutive Equation = {model_name}
Description / Usage¶
This required card is used to specify the polymer constitutive equation. A single input parameter must be defined, that being the {model_name}.
- {model_name}
Name of the constitutive equation model, being one of the following values: NOPOLYMER, OLDROYDB, GIESEKUS, PTT, SARAMITO_OLDROYDB, SARAMITO_GIESEKUS, SARAMITO_PTT, WHITE-METZNER. Several of these polymer constitutive models require additional parameters for the polymer properties that are entered via additional cards, as described below. Please see the Example sectionand the tutorial referenced below.
Thus,
- NOPOLYMER
For Newtonian and generalized Newtonian models. No floating point values are required.
- OLDROYDB
For the Oldroyd-B constitutive model. This option requires four floating point values, which are described below.
- GIESEKUS
For the Giesekus model. This option requires five floating point values, which are described below.
- PTT
For the Phan-Thien Tanner model. This option requires six floating point values, which are described below.
- SARAMITO_OLDROYDB
For the Oldroyd-B model used with the Saramito yield model. This option requires six floating point values, which are described below.
- SARAMITO_GIESEKUS
For the Giesekus model used with the Saramito yield model. This option requires seven floating point values, which are described below.
- SARAMITO_PTT
For the Giesekus model used with the Saramito yield model. This option requires eight floating point values, which are described below.
- WHITE_METZNER
For the White-Metzner model. This option is not currently working.
Examples¶
The following is a sample card that sets the polymer constitutive equation to NOPOLYMER. This option does not require any additional cards since it indicates that there is no polymer constitutive equation present.
Polymer Constitutive Equation = NOPOLYMER
The following is a sample card that sets the polymer constitutive equation to OLDROYDB. This option requires four cards describing the polymer stress formulation, weight function, viscosity and time constant.
Polymer Constitutive Equation = OLDROYDB
Polymer Stress Formulation = EVSS_F
Polymer Weight Function = GALERKIN
Polymer Viscosity = CONSTANT 1.
Polymer Time Constant = CONSTANT 0.02
The following is a sample card that sets the polymer constitutive equation to GIESEKUS. This option requires five cards describing the polymer stress formulation, weight function, viscosity, time constant and mobility parameter.
Polymer Constitutive Equation = GIESEKUS
Polymer Stress Formulation = EVSS_F
Polymer Weight Function = GALERKIN
Polymer Viscosity = CONSTANT 1.
Polymer Time Constant = CONSTANT 0.2
Mobility Parameter = CONSTANT 0.1
The following is a sample card that sets the polymer constitutive equation to PHANTHIEN TANNER (or PTT). This option requires six additional cards that set the polymer stress formulation, weight function for the stress equation, viscosity, time constant and nonlinear PTT parameters.:
Polymer Consitutive Equation = PTT
Polymer Stress Formulation = EVSS_F
Polymer Weight Function = GALERKIN
Polymer Viscosity = CONSTANT 8000.
Polymer Time Constant = CONSTANT 0.01
PTT Xi parameter = CONSTANT 0.10
PTT Epsilon parameter = CONSTANT 0.05
The following is a sample card that sets the polymer constitutive equation to SARAMITO_OLDROYDB. This option requires six cards describing the polymer stress formulation, weight function, viscosity, time constant, yield stress, and yield exponent.
Polymer Constitutive Equation = SARAMITO_OLDROYDB
Polymer Stress Formulation = EVSS_F
Polymer Weight Function = GALERKIN
Polymer Viscosity = CONSTANT 1.
Polymer Time Constant = CONSTANT 0.02
Polymer Yield Stress = CONSTANT 15.
Yield Exponent = CONSTANT 0.
The following is a sample card that sets the polymer constitutive equation to SARAMITO_GIESEKUS. This option requires seven cards describing the polymer stress formulation, weight function, viscosity, time constant, mobility parameter, yield stress, and yield exponent.
Polymer Constitutive Equation = SARAMITO_GIESEKUS
Polymer Stress Formulation = EVSS_F
Polymer Weight Function = GALERKIN
Polymer Viscosity = CONSTANT 1.
Polymer Time Constant = CONSTANT 0.2
Polymer Yield Stress = CONSTANT 12.
Yield Exponent = CONSTANT 1.0
Mobility Parameter = CONSTANT 0.1
The following is a sample card that sets the polymer constitutive equation to SARAMITO_PTT. This option requires eight additional cards that set the polymer stress formulation, weight function for the stress equation, viscosity, time constant, nonlinear PTT parameters, yield stress, and yield exponent.
Polymer Consitutive Equation = SARAMITO_PTT
Polymer Stress Formulation = EVSS_F
Polymer Weight Function = GALERKIN
Polymer Viscosity = CONSTANT 8000.
Polymer Time Constant = CONSTANT 0.01
Polymer Yield Stress = CONSTANT 200.
Yield Exponent = CONSTANT 0.5
PTT Xi parameter = CONSTANT 0.10
PTT Epsilon parameter = CONSTANT 0.05
The following is a sample card that sets the polymer constitutive equation to WHITE_METZNER. This option is not currently functional for multimode viscoelasticity. If needed it could be resurrected with only minimal changes to the input parser.
Polymer Consitutive Equation = WHITE_METZNER
Technical Discussion¶
The viscoelastic tutorial is helpful for usage issues such as extensions from single mode to multimodes.
References¶
GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao
Polymer Stress Formulation¶
Polymer Constitutive Equation = {model_name}
Description / Usage¶
This card specifies which formulation of the polymer constitutive equation should be used. Valid options are
EVSS_G |
Uses the classic elastic-viscous stress splitting of Rajagopalan (1990) where the stress is the elastic stress only without a Newtonian component. This option is the default if this Polymer Stress Formulation card is not supplied. This formulation is almost never used. |
EVSS_F |
Uses the EVSS formulation of Guenette and Fortin (1995) that solves the standard stress equation with the addition of a new term to the momentum equation. This formulation is used most often. |
EVSS_L |
Uses a research formulation for viscoelasticity that includes a level set discretization that switches the equations from solid to fluid. This option is not currently in production usage. |
Examples¶
The following is a sample card that sets the polymer stress formulation to EVSS_F:
Polymer Stress Formulation = EVSS_F
Technical Discussion¶
No Discussion.
References¶
Guenette, R. and M. Fortin, “A New Mixed Finite Element Method for Computing Viscoelastic Flow,” J. Non-Newtonian Fluid Mech., 60 (1995) 27-52.
Rajagopalan, D., R. C. Armstrong and R. A. Brown, “Finite Element Methods for Calculation of Viscoelastic Fluids with a Newtonian Viscosity”, J. Non-Newtonian Fluid Mech., 36 (1990) 159-192.
Polymer Weight Function¶
Polymer Weight Function = {GALERKIN | SUPG}
Description / Usage¶
This optional card is used to specify the weight function for the polymer stress equation. Valid options are
GALERKIN |
Uses a Galerkin weight-function for the stress equation. This option is the default if this card is not present. |
SUPG |
Uses a streamline upwind Petrov-Galerkin weight-function for the stress equation. If this option is chosen, a weight must be specified via the Polymer Weighting card. |
Examples¶
The following is a sample card that set the polymer weight function to SUPG and demonstrates the required cards.
Polymer Weight Function = SUPG
Polymer Weighting = CONSTANT 0.1
The following is a sample card that set the polymer weight function to GALERKIN.
Polymer Weight Function = GALERKIN
Technical Discussion¶
No Discussion.
Polymer Shift Function¶
Polymer Shift Function = {CONSTANT | MODIFIED_WLF} <float1> [float2]
Description / Usage¶
This optional card is used to specify the temperature shift function for the polymer relaxation times and viscosities in the polymer stress equation(s);
Valid options are
CONSTANT |
Applies a constant temperature shift factor to the polymer relaxation time(s) and the polymer viscosities.
|
This option may be useful for continuation in elasticity level since continuation in this parameter will uniformly increase or decrease the relaxation time(s) and viscosities of all viscoelastic modes.
MODIFIED_WLF |
Applies a temperature shift factor which is a modified version of the Williams-Landel-Ferry shift model (cf. Bird, Armstrong, and Hassager 1987, pp.139-143); The reference temperature, Tref, is taken from the Reference Temperature card. Note that if C2 is chosen equal to Tref, this model reduces to an Arrhenius form where C1 = Eμ/RTref. Also note that this form is based on the exponential function whereas the WLF model is based on 10x.
|
Examples¶
The following is a sample card that sets a constant temperature shift.
Polymer Shift Function = CONSTANT 1.0
The following is a sample card that utilizes the modified WLF shift function.
Polymer Shift Function = MODIFIED_WLF 2.5 95.0
Technical Discussion¶
No Discussion.
References¶
Bird, R. B., Armstrong, R. C., and Hassager, O. Dynamics of Polymeric Liquids, Volume 1. John Wiley & Sons, Inc. 1987.
Polymer Weighting¶
Polymer Weighting = <float> [t/L]
Description / Usage¶
This card is only used if the value of the Polymer Weight Function card is SUPG. The single input parameter is defined as
<float> - scale factor for the upwind term in the Petrov-Galerkin formulation. If this is set to zero, a Galerkin weight function is used. The correct scaling for this term is the inverse of the average inflow velocity.
Examples¶
The following is a companion pair of sample input cards that includes setting the polymer weighting to 0.1:
Polymer Weight Function = SUPG
Polymer Weighting = 0.1
Technical Discussion¶
No Discussion.
References¶
No References.
Discontinuous Jacobian Formulation¶
Discontinuous Jacobian Formulation = {model_name} <float>
Description / Usage¶
This optional card is used to specify the off element Jacobian contributions for the discontinuous Galerkin (DG) discretization of the polymer stress equation. These terms are important because the DG method uses stress information from upstream elements to determine the flux in the current element. If the off element Jacobians are not included, convergence is poor, but including these terms greatly increases the complexity of the code, the matrix bandwidth and the matrix solution time.
The default sets this option to false, implying that no off element Jacobians are included. Valid options for {model_name} are:
FULL |
adds in the full complement of off-element Jacobians; no floating point data required. This option does not always work in parallel computations. |
EXPLICIT |
approximates the off-element Jacobians by adding terms to the residual equation based on the previous iteration.
|
SEGREGATED |
approximates the off-element Jacobians by adding terms to the residual equation based on a mass lumping at the current iteration.
|
Examples¶
The following is a sample card that set the discontinuous Jacobian formulation to full.
Discontinuous Jacobian Formulation = FULL
The following is a sample card that set the discontinuous Jacobian formulation to explicit. Note this is more of a research option than a production one and the choice of scaling requires tuning for each problem.
Discontinuous Jacobian Formulation = EXPLICIT 0.1
The following is a sample card that set the discontinuous Jacobian formulation to segregated. Note this is more of a research option than a production one and the choice of scaling requires tuning for each problem.
Discontinuous Jacobian Formulation = SEGREGATED 0.2
Technical Discussion¶
For a discussion of the discontinuous Galerkin method see Fortin and Fortin (1989), Baaijens (1994) or Baaijens (1998). Internal (Sandia) users may find T. A. Baer’s Gordon Conference presentation (1997) helpful.
References¶
Baaijens, F. P. T. , “Application of Low-Order Discontinuous Galerkin Method to the Analysis of Viscoelastic Flows,” J. Non-Newtonian Fluid Mech., 52, 37-57 (1994).
Baaijens, F. P. T., “An Iterative Solver for the DEVSS/DG Method with Application to Smooth and Non-smooth Flows of the Upper Convected Maxwell Fluid,” J. Non- Newtonian Fluid Mech., 75, 119-138 (1998).
Fortin, M. and A. Fortin, “A New Approach for the FEM Simulations of Viscoelastic Flow, J. Non-Newtonian Fluid Mech., 32, 295-310 (1989).
Adaptive Viscosity Scaling¶
Adaptive Viscosity Scaling = CONSTANT <float>
Description / Usage¶
This optional card is used to specify the adaptive viscosity scaling and the ε parameter associated with its usage (see theory section below). It requires one floating point number that scales the term. Definitions of the input parameters are as follows:
CONSTANT |
Name of the model for the adaptive viscosity scaling.
|
Examples¶
The following is a sample card that sets the adaptive viscosity scaling to 0.5:
Adaptive Viscosity Scaling = CONSTANT 0.5
Technical Discussion¶
The momentum equation is modified with the addition of a numerical adaptive viscosity to help maintain the elliptic character of the equation set as stress and velocity gradient increase
where ηs is the solvent viscosity and ηp is the polymer viscosity. If we set the adaptive viscosity to zero (ηa= 0), we obtain the Standard EVSS Formulation of Guenette and Fortin (1995). For adaptive viscosity, we use the following definition
with 0<ε<1.
The equations are unchanged in the limit of h, the element size, going to zero.
Please see the viscoelastic tutorial for a discussion of usage for the adaptive viscosity scaling. The papers by Sun, et. al. (1996) and Sun, et. al (1999) provide a good discussion of the theory behind its usage. CRMPC presentations by R.R. Rao demonstrates its usefulness for Goma calculations.
References¶
GT-014.1: Tutorial for Running Viscoelastic Flow Problems with GOMA, June 21, 2000, R. R. Rao
Guenette, R. and M. Fortin, “A New Mixed Finite Element Method for Computing Viscoelastic Flows,” J. Non-Newtonian Fluid Mech., 60, 27-52 (1995).
Sun, J., N. Phan-Thien, R. I. Tanner, “An Adaptive Viscoelastic Stress Splitting Scheme and Its Applications: AVSS/SI and AVSS/SUPG,” J. Non-Newtonian Fluid Mech., 65, 75-91 (1996).
Sun, J., M. D. Smith, R. C. Armstrong, R. A. Brown, “Finite Element Method for Viscoelastic Flows Bases on the Discrete Adaptive Viscoelastic Stress Splitting and the Discontinuous Galerkin Method: DAVSS-G/DG,” J. Non-Newtonian Fluid Mech., 86, 281-307 (1999).
Polymer Viscosity¶
Polymer Viscosity = {model_name} <float> [M/Lt]
Description / Usage¶
This card is used to specify the polymer viscosity associated with the model set in the Polymer Constitutive Equation card. This is a required card for the OLDROYDB, GIESEKUS and PTT models.
Definitions of the input parameters are as follows:
{model_name} |
Permissible names for the viscosity model are CONSTANT, POWER_LAW and CARREAU. |
CONSTANT |
a simple constant viscosity, Newtonian fluid. |
POWER_LAW |
a power-law model |
CARREAU |
a Carreau strain-rate thinning or thickening relation |
Input parameters are not identified for the latter two models as they have not worked since the multimode port. They could be made to work again if the proper tweaking is done to the input parser, but are not currently functional.
Examples¶
The following is a sample card that sets the polymer viscosity to 8000.0:
Polymer Viscosity = CONSTANT 8000.0
Technical Discussion¶
No Discussion.
References¶
Polymer Time Constant¶
Polymer Time Constant = {model_name} <float> [t]
Description / Usage¶
This card is used to specify the polymer time constant associated with the Polymer Constitutive Equation card. It is a required card for the OLDROYDB, GIESEKUS and PTT options. Definitions of the input parameters are as follows:
Definitions of the input parameters are as follows:
{model_name} |
Permissible names for the viscosity model are CONSTANT, POWER_LAW and CARREAU. |
CONSTANT |
a simple constant viscosity, Newtonian fluid. |
POWER_LAW |
a power-law model |
CARREAU |
a Carreau strain-rate thinning or thickening relation |
Input parameters are not identified for the latter two models as they have not worked since the multimode port. They could be made to work again if the proper tweaking is done to the input parser, but are not currently functional.
If the polymer time constant varies with properties, it must do so in the same way as the polymer viscosity; thus, the model on this card must be the same as the model selected on the Polymer Viscosity card.
All three models are described in detail in Bird, et. al. (1987).
Examples¶
The following is a sample card that sets the polymer time constant to 1.0:
Polymer Time Constant = CONSTANT 1.0
Technical Discussion¶
No Discussion.
References¶
Bird, R. B., Armstrong, R. C., and Hassager, O. 1987. Dynamics of Polymeric Liquids, 2nd ed., Wiley, New York, Vol. 1.
Polymer Yield Stress¶
Polymer Yield Stress = CONSTANT <float> []
Description / Usage¶
This card is required when using the Saramito yield model. The card should be included in the input when the option selected for the Polymer Constitutive Equation card is SARAMITO_OLDROYDB, SARAMITO_GIESEKUS, or SARAMITO_PTT. Definitions of the input parameters are as follows:
- CONSTANT <float>
Name of the model for the yield stress. * <float> - the value of the yield stress.
This card does not have to be present for constitutive equations other than SARAMITO_OLDROYDB, SARAMITO_GIESEKUS, and SARAMITO_PTT
Examples¶
The following is a sample card that sets the polymer yield stress to 12:
Polymer Yield Stress = CONSTANT 12
Mobility Parameter¶
Mobility Parameter = CONSTANT <float> []
Description / Usage¶
This card is used in the Giesekus model in the nonlinear stress terms. The card should be included in the input when the option selected for the Polymer Constitutive Equation card is GIESEKUS. Definitions of the input parameters are as follows:
CONSTANT |
Name of the model for the mobility parameter.
|
This card does not have to be present for constitutive equations other than GIESEKUS.
Examples¶
The following is a sample card that sets the mobility parameter to 0.2:
Mobility Parameter = CONSTANT 0.2
Technical Discussion¶
No Discussion.
PTT Xi parameter¶
PTT Xi parameter = {model_name} <float>
Description / Usage¶
This card is used in the Phan-Thien Tanner model in the nonlinear stress terms. The card should be included in the input when the option selected for the Polymer Constitutive Equation card is PTT. Definitions of the input parameters are as follows:
CONSTANT |
Name of the model for PTT Xi parameter.
|
This card does not have to be present for constitutive equations other than PTT.
Examples¶
The following is a sample card that sets the PTT Xi parameter to 0.1:
PTT Xi parameter = CONSTANT 0.10
Technical Discussion¶
No Discussion.
PTT Epsilon parameter¶
PTT Epsilon parameter = {model_name} <float>
Description / Usage¶
This card is used in the Phan-Thien Tanner model in the nonlinear stress terms. The card should be included in the input when the option selected for the Polymer Constitutive Equation card is PTT. Definitions of the input parameters are as follows:
CONSTANT |
Name of the model for PTT Epsilon parameter.
|
This card does not have to be present for constitutive equations other than PTT.
Examples¶
The following is a sample card that sets the PTT Epsilon parameter to 0.1:
PTT Xi parameter = CONSTANT 0.10
Technical Discussion¶
No Discussion.
Surface Tension¶
Surface Tension = {CONSTANT | DILATION | USER} <float_list> [M/t2]
Description / Usage¶
This card is used to specify the interfacial surface tension of the fluid which enters into the CAPILLARY boundary condition and CAP_ENDFORCE boundary condition cards. The surface tension, albeit a property of an interface and not of a bulk material, is sometimes influenced by thermophysical phenomena associated with a material, hence the inclusion of this card in the material file. It should be mentioned that this card is optional, and if it does not appear the surface tension is taken off the aforementioned boundary condition cards. PLEASE see the important technical discussion below if you plan on using this card. Definitions of the input parameters are as follows:
CONSTANT |
Name of the model for a constant value of interfacial surface tension of the fluid:
|
DILATION |
Name of a surface tension model that depends on mesh dilation (only useful if the free surface is constrained to be a material surface both normally and tangentially, see Schwartz ,et. al. 1996). The model mathematically is |
USER |
A user-defined surface tension model that is defined in the user-supplied routine usr_surface_tension in the file user_mp.c. This model will have an arbitrary number of user-defined parameters (<float1> to floatn>). |
WARNING: When specifying surface tension on this card, be sure the surface tension (multiplier) on the boundary condition CAPILLARY card is set to 1. In other words, the value of surface tension on the boundary condition cards is multiplied with the value on this card before the calculation is carried out.
Technical Discussion¶
Please read and understand the warning issued above regarding the proper place to specify surface tension. Basically, for constant surface tension models, it is a good idea to leave this card out and simply enter the proper surface tension value for the current surface on the boundary condition cards CAPILLARY and CAP_ENDFORCE. For variable models, please set the surface tension values on these BC cards to 1.0, and then handle your model through this card. The surface tension is a thermodynamic property of the interface and actually depends on the chemical composition of the fluids (or fluid/solids) of the bounding phases. The property controls the importance of the capillary stress jump on a curved interface on the hydrodynamics of the flow and the meniscus position and motion.
References¶
GT-001.4: GOMA and SEAMS tutorial for new users, February 18, 2002, P. R. Schunk and D. A. Labreche
Second Level Set Conductivity¶
Second Level Set Conductivity = {model_name} {float_list} {char_string} [M/Lt]
Description / Usage¶
This card allows to the user to specify a second thermal conductivity model that will be applied to one side of a level set interfacial curve:
{model_name} |
The name of the conductivity model can only be CONSTANT at the current time. |
{float1} |
This is a single float parameter which is the value of Fourier thermal conducticity applied to the second level set phase fluid. |
{char_string} |
This string may take the values POSITIVE or NEGATIVE. It identifies which side of the interface the preceding conductivity model is applied to. |
This card allows the user to apply a CONSTANT or USER model to one side of the interface while the other side recieves the constant conductivity value listed on this card. The side of the interface that corresponds to char_string appearing on this card receives the constant conductivity value. The opposite side’s conductibity is determined from the other, (possibly) more complex model. Transition between them is accomplished using smooth Heaviside functions whose width is given on the Level Set Length Scale card. Note that it is the prescence of the this card in the material file that actually activates this selection process.
Examples¶
The following is a usage example for this card:
Conductivity = USER 1.e4 0.1 3.0
Second Level Set Conductivity = CONSTANT. 1.0e-4 POSITIVE
This setup will cause the negattive side of the interface to receive conductivity values obtained from the USER model with the parameters listed above . The positive side of the interface will show a constant conductivity of 1.0e-4.
Technical Discussion¶
No Discussion.
References¶
No References.
Second Level Set Density¶
Second Level Set Density = {model_name} {float_list} {char_string} [M/Lt]
Description / Usage¶
This card allows to the user to specify a second density model that will be applied to one side of a level set interfacial curve:
{model_name} |
The name of the density model can only be CONSTANT at the current time. |
{float1} |
This is a single float parameter which is the value of density applied to the second level set phase fluid. |
{char_string} |
This string may take the values POSITIVE or NEGATIVE. It identifies which side of the interface the preceding density model is applied to. |
This card allows the user to apply one of the several complex density models currently available in Goma to one side of the interface while the other side recieves the constant density value listed on this card. The side of the interface that corresponds to char_string appearing on this card recieves the constant density value. The opposite sides density is determined from the other, more complex model. Transition between them is accomplished using smooth Heaviside functions whose width is given on the Level Set Length Scale card. Note that it is the prescence of the this card in the material file that actually activates this selection process.
Examples¶
The following is a usage example for this card:
Density = SUSPENSION 1.0 1.0 1.0
Second Level Set Density = CONSTANT. 1.0 POSITIVE
This setup will cause the negattive side of the interface to receive density values obtained from the SUSPENSION model with the parameters listed above . The positive side of the interface will show a constant density of 1.0.
Technical Discussion¶
No Discussion.
Second Level Set Heat Capacity¶
Second Level Set Heat Capacity = {model_name} {float_list} {char_string} [M/Lt]
Description / Usage¶
This card allows to the user to specify a second thermal heat capacity model that will be applied to one side of a level set interfacial curve:
{model_name} |
The name of the heat capacity model can only be CONSTANT at the current time. |
{float1} |
This is a single float parameter which is the value of heat capacity applied to the second level set phase fluid. |
{char_string} |
This string may take the values POSITIVE or NEGATIVE. It identifies which side of the interface the preceding heat capacity model is applied to. |
This card allows the user to apply a CONSTANT or USER model to one side of the interface while the other side recieves the constant heat capacity value listed on this card. The side of the interface that corresponds to char_string appearing on this card receives the constant heat capacity value. The opposite side’s heat capacity is determined from the other, (possibly) more complex model. Transition between them is accomplished using smooth Heaviside functions whose width is given on the Level Set Length Scale card. Note that it is the prescence of the this card in the material file that actually activates this selection process.
Examples¶
The following is a usage example for this card:
Heat Capacity = ENTHALPY 1.e4 0.1
Second Level Set Heat Capacity = CONSTANT. 1.0 POSITIVE
This setup will cause the negattive side of the interface to receive heat capacity values obtained from the USER model with the parameters listed above . The positive side of the interface will show a constant heat capacity of 1.0e-4.
Technical Discussion¶
No Discussion.
Second Level Set Momentum Source¶
Second Level Set Momentum Source = {model_name} {float_list} {char_string} [M/Lt]
Description / Usage¶
This card allows to the user to specify a second thermal Navier-Stokes volumetric momentum source model that will be applied to one side of a level set interfacial curve:
{model_name} |
The name of the momentum source model can only be CONSTANT at the current time. |
{float1} |
This is a single float parameter which is the value of volumetric momentum source term applied to the second level set phase fluid.[F/L3] |
{char_string} |
This string may take the values POSITIVE or NEGATIVE. It identifies which side of the interface the preceding momentum source model is applied to. |
This card allows the user to apply one of the several momentum source models implement in Goma to one side of the interface while the other side recieves the constant momentum source value listed on this card. The side of the interface that corresponds to char_string appearing on this card receives the constant momentum source value. The opposite side’s momentum source is determined from the other, (possibly) more complex model. Transition between them is accomplished using smooth Heaviside functions whose width is given on the Level Set Length Scale card. Note that it is the prescence of the this card in the material file that actually activates this selection process.
Examples¶
The following is a usage example for this card:
Navier-Stokes Source = SUSPEND 0. 0. -980.0 1.34e3
Second Level Set Momentum Source = CONSTANT. 1.0e-4 POSITIVE
This setup will cause the negattive side of the interface to receive momentum source values obtained from the USER model with the parameters listed above . The positive side of the interface will show a constant momentum source of 1.0e-4.
Technical Discussion¶
An important thing to note is that the units of the quantity specified on this card are units of force per volume in exact correspondence to the units used with the preceding momentum source model. Note also that this card should not be used when using the LEVEL_SET momentum source model. For one thing, it makes no sense and for another thing the values specified on the latter model are simply the gravitational acceleration and therefore are inconsistent with this card.
Second Level Set Viscosity¶
Second Level Set Viscosity = {model_name} {float_list} {char_string} [M/Lt]
Description / Usage¶
This card allows to the user to specify a second viscosity model that will be applied to one side of a level set interfacial curve:
{model_name} |
The name of the viscosity model can only be CONSTANT at the current time. |
{float1} |
This is a single float parameter which is the value of Newtonian viscosity applied to the second level set. phase fluid. |
{char_string} |
This string may take the values POSITIVE or NEGATIVE. It identifies which side of the interface the preceding viscosity model is applied to. |
This card allows the user to apply one of the several complex viscosity models currently available in Goma to one side of the interface while the other side recieves the constant viscosity value listed on this card. The side of the interface that corresponds to char_string appearing on this card recieves the constant viscosity value. The opposite sides viscosity is determined from the other, more complex model. Transition between them is accomplished using smooth Heaviside functions whose width is given on the Level Set Length Scale card. Note that it is the prescence of the this card in the material file that actually activates this selection process.
Examples¶
The following is a usage example for this card:
Liquid Constitutive Equation = HERSCHEL_BULKLEY
Low Rate Viscosity = CONSTANT 10000
Power Law Exponent = CONSTANT 0.6
Yield Stress = CONSTANT 1.e6
Second Level Set Viscosity = CONSTANT. 1.0 POSITIVE
This setup will cause the negattive side of the interface to receive viscosity values obtained from the HERSCHEL_BULKLEY model with the parameters listed above . The positive side of the interface will show a constant viscosity of 1.0.
Technical Discussion¶
No Discussion.
References¶
No References.
Shell Bending Stiffness¶
Shell bending stiffness = {model_name} {float_list} [M/Lt2]
Description / Usage¶
This required card is used to specify the model for the Shell bending stiffness property D which is defined as D=Et3/12(1-ν2), where E is the elastic modulus, ν Poisson’s ratio, and t the shell thickness. The units are M-L2/t2 (or F-L). The elastic modulus is set through the Lame MU and Lame Lambda cards. This property is needed for the inextensible cylindrical shell equations (see EQ = Shell Tension).
Definitions of the input parameters are as follows:
{model_name} |
Name of the Shell bending stiffness coefficient model. This parameter can have one of the following values: CONSTANT.
|
The details of each model option are given below:
CONSTANT <float1> |
For the CONSTANT model, {float_list} is a single value:
|
References¶
GT-027.1: GOMA’s Shell Structure Capability: User Tutorial (GT-027.0). P. R. Schunk and E. D. Wilkes.
GT-033.0: Structural shell application example: tensioned-web slot coater (GT-033.0). P. R. Schunk and E. D. Wilkes.