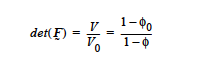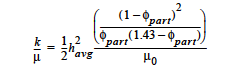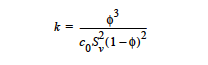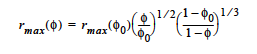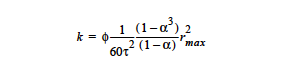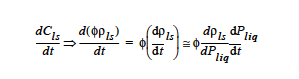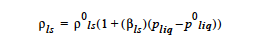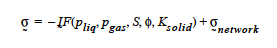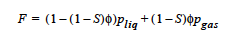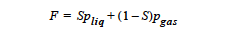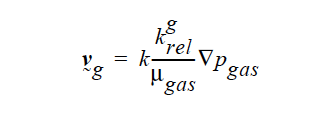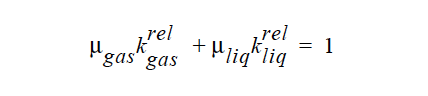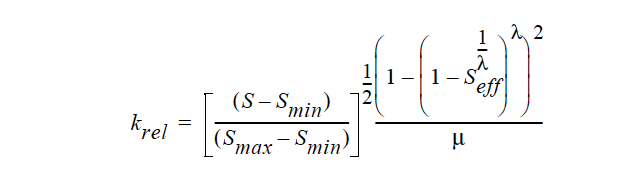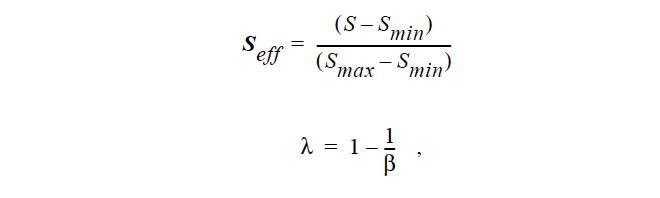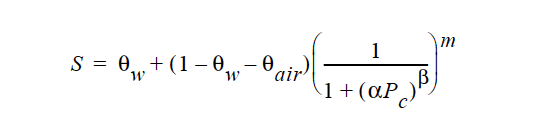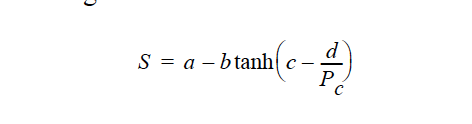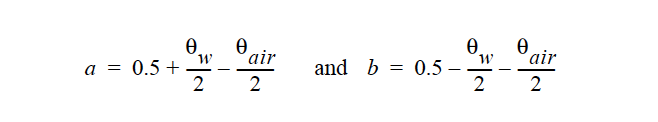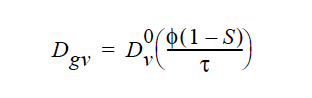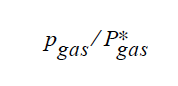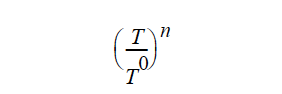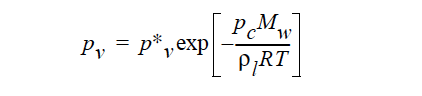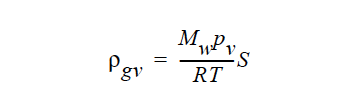Microstructure Properties¶
Microstructure property models address material parameters and constitutive equations required for multiphase continuum approaches to flow in porous media, viz. fluid flow in partially or fully saturated porous media. Actually, only a few of these model/property cards pertain directly to media structure or microstructure, but all are affected by intrinsic material properties of all involved phases. Cards or records typically appearing in this section fall into one of three categories: microstructural or flow-property specification, numerical treatment specification, and species transport property specifications. These “sections” appear in this order in most of the sample input files.
Media Type¶
Media Type = {model_name}
Description / Usage¶
This card is used to designate the characteristic medium type for solid materials so that the proper microstructural features/models may be imposed. Basically, the choices are dictated by whether the medium is to be modeled as porous (viz. a medium in which flow will be determined relative to the motion of a porous solid skeleton) or as continuous (viz., in which the mechanics equations apply to all parts of the medium and not weighted by a solid fraction). If porous flow through Darcy or Brinkman formulations are desired in the material, then the phase is designated as continuous.
The input parameter is a {model_name} and has the following possible values:
{model_name} |
{model_name} Name of the media model; the choices are
|
Specific characteristics of these types are identified below, including other cards that must be present.
If the type chosen is CONTINUOUS, then the material is assumed to be amorphous and no further microstructure properties need to be specified (next required card is the Diffusion Constitutive Equation).
In a porous medium with one phase in the pores (i.e. a saturated medium), use POROUS_SATURATED then only the Porosity and Permeability cards are required. A POROUS_SATURATED medium model enables the user to solve the simplest porous flow equation for the liquid phase pressure only for rigid porous media (see the porous_sat or porous_liq equation cards). For deformable porous saturated media, one can employ a stress balance and porosity equation for deformable porous media (see mesh* equation cards and porous_deform equation card).
In a porous medium with two phases in the pores (such as air-water, i.e., an unsaturated medium), two options exist - POROUS_UNSATURATED, a formulation of the porous flow problem using the capillary pressure as the field variable (gas pressure assumed to be uniform), and POROUS_TWO_PHASE, a formulation of the porous flow problem using the liquid pressure and gas pressure as field variables. All the cards in this Microstructure porous flow section, except the Brinkman cards (FlowingLiquid Viscosity and Inertia Coefficient), are needed for the unsaturated or two-phase models. As in the saturated case above, these options can also be chosen for deformable porous media, for which the Lagrangian mesh stress equations and the porosity equation are used to complete the effective stress principle formulation.
The POROUS_BRINKMAN model is an extension of the Navier-Stokes equation for porous media. In addition, it has an inertia term intended to account for boundary and interface deficiencies at Reynold’s numbers greater than one (Re > 1), a deficiency in all Darcy flow models (see, e.g., Gartling, et. al., 1996). It is a vector formulation (the momentum equations) of saturated flow in a porous medium which reduces to the Navier-Stokes equations as the porosity increases to one (φ → 1). For Brinkman flow, the input parameters (i.e., cards) that must be specified from this section are Porosity, Permeability, FlowingLiquid Viscosity, and Inertia Coefficient. Please note the use of two viscosities; for the Brinkman media type, the viscosity entered via the (Mechanical Properties and Constitutive Equations) Viscosity card is interpreted to be the Brinkman viscosity (μB) and is used to calculate the viscous stresses (see Gartling, et. al., 1996) while the FlowingLiquid Viscosity (μ) is used in the correction term for nonlinear drag forces in porous media. Brinkman viscosity is an effective value and can be taken as the porosity weighted average of the matrix and fluid. It is generally not correct to set it equal to the liquid viscosity (Martys, et. al., 1994; Givler and Altobelli, 1994).
The POROUS_SHELL_UNSATURATED model is used for thin shell, open pore, porous media, viz. the shell_sat_open equation. This media type instructs GOMA to obtain most of the media properties from the bulk continuum specifications just like POROUS_UNSATURATED. Exceptions are the Porous Shell Cross Permeability model and the Porous Shell Height material models. Please see the porous shell tutorial
Examples¶
Following is a sample card:
Media Type = POROUS_TWO_PHASE
This card will require a plethora of material models for Darcy flow of liquid and gas in a porous medium. It also will require the use of two Darcy flow mass balances in the Problem Description EQ specification section, specifically porous_liq and porous_gas equations. See references below for details.
Technical Discussion¶
In solving porous medium problems, it is important to understand that each conservation equation represents a component, or species balance. The porous_liq equation is actually a species balance for the liquid phase primary component (e.g. water) for all phases in the medium, viz. liquid, gas, and solid. This is the case even though the dependent variable is the liquid phase pressure. This is the only required equation for rigid POROUS_SATURATED media. The same holds true for rigid POROUS_UNSATURATED media, as the liquid solvent is present in liquid and gas vapor form (it is actually taken as insoluble in the solid). For deformable media, one must add a stress balance through the mesh* equations (in LAGRANGIAN form, as described on the Mesh Motion card) and a solid phase “solvent” balance which is used to solve for the porosity, viz. the porous_deform equation. In these cases, the gas is taken to be at constant pressure. If pressure driven Darcy flow is important in the gas, an additional species balance for the primary gas component is required through the porous_gas equation. This last case is the so-called POROUS_TWO_PHASE media type.
Options for representing the solid medium as rigid or deformable are discussed under the Saturation, Permeability and Porosity cards. When rigid porous media are modeled, both porosity and permeability are constant. In Goma 4.0, these concepts were being researched and improved, with much of the usage documentation residing in technical memos.
References¶
GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk
GT-009.3: GOMA’s capabilities for partially saturated flow in porous media, September 1, 2002, P. R. Schunk
Gartling D. K., C. E. Hickox and R. C. Givler 1996. “Simulations of Coupled Viscous and Porous Flow Problems”, Comp. Fluid Dynamics, 7, 23-48.
Givler, R. C. and S. A. Altobelli 1994. “A Determination of the Effective Viscosity for the Brinkman-Forchheimer Flow Model.” J. Fluid Mechanics, 258, 355-370.
Martys, N., D. P. Bantz and E. J. Barboczi 1994. “Computer Simulation Study of the Effective Viscosity in Brinkman’s Equation.” Phys. Fluids, 6, 1434-1439
Porosity¶
Porosity = {model_name} <float> []
Description / Usage¶
This card is used to specify the model for the porosity, which is required for the Brinkman or Darcy formulations for flow through porous media, viz. for POROUS_BRINKMAN, POROUS_TWO_PHASE, POROUS_SATURATED, and POROUS_UNSATURATED media types (see Media Type card).
Definitions of the {model_name} and <float> parameters are as follows:
CONSTANT |
Name {model_name} of the constant porosity model.
|
DEFORM |
Name {model_name} of the model for a porosity that varies with deformation of the porous medium. A conservation balance is required for the solid material skeleton and is invoked in the equation specification section (see EQ section).
|
Examples¶
The following is a sample input card:
Porosity = DEFORM 0.5
This model will result in a porosity of 0.5 (volume fraction of the interstitial space of a porous skeleton) in the undeformed or stress-free state, but will allow the porosity to vary affinely with the volume change invariant of the deformation gradient tensor (see technical discussion). As mentioned above, the DEFORM model requires a field equation for the mass-conservation of the solid matrix through the porous_deform equation.
Technical Discussion¶
Porosity is a microstructural attribute of a porous medium which describes the fraction of volume not occupied by the solid skeleton. For rigid porous media, it is a parameter that weights the capacitance term (time-derivative term) of the Darcy flow equations for liquid solvent and gas “solvent” concentrations. It often affects the Saturation function (see Saturation card) and the permeability function (see Permeability card). The references cited below elucidate the role of the porosity parameter in these equations.
For deformable porous media, Goma uses the porosity as a measure of fraction solid concentration, as a part of a mass balance for the solid skeleton. The reason this equation is required is a result of the lack of an overall conservation law for the mixture. Instead, we close the system by individual conservation equations for all species components in the medium, including the solid; the liquid and gas phase components are accounted for with individual Darcy flow equations. The conservation law which governs the porosity assumes there is an affine deformation of the pores with the overall deformation of the solid, and hence can be written as:
where F˜ is the deformation gradient tensor, φ0 is the initial porosity, and φ is the porosity. This equation is invoked with the porous_deform option on the EQ specifications.
References¶
GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk
GT-009.3: GOMA’s capabilities for partially saturated flow in porous media, September 1, 2002, P. R. Schunk
SAND96-2149: Drying in Deformable Partially-Saturated Porous Media: Sol-Gel Coatings, Cairncross, R. A., P. R. Schunk, K. S. Chen, S. S. Prakash, J. Samuel, A. J. Hurd and C. Brinker (September 1996)
Permeability¶
Permeability = {model_name} {float_list} [L2]
Description / Usage¶
This card is used to specify the model for permeability, which is required for the Brinkman and Darcy formulations for flow through porous media. Definitions of the input parameters are as follows:
{model_name} |
Name of the permissible models for permeability: CONSTANT, TENSOR, KOZENY_CARMEN, SOLIDIFICATION and PSD_VOL, PSD_WEXP, or PSD_SEXP. (No USER model as of 6/13/2002; contact Developers for this addition). |
{float_list} |
One or more floating point numbers (<float1> through <floatn>) whose values are determined by the selection for {model_name}. |
Permeability model choices and their parameters are discussed below.
CONSTANT <float1> |
Model for constant permeability with a single parameter. This model is allowed for all Media Types (cf. Media Type card).
|
TENSOR <float1> <float2> <float3> <float4> |
Model for a two dimensional, constant anisotropic permeability; it has not been implemented in three dimensions. All media types (cf. Media Type card) except POROUS_BRINKMAN may use this model.
|
PSD_VOL <float1> <float2> <float3> <float4> |
This is a model of a deformable medium with a probabilistic distribution of pore sizes; see Technical Discussion section. Four parameters are required for the PSD_VOL model:
All media types (cf. Media Type card) except POROUS_BRINKMAN may use this model |
PSD_WEXP <float1> <float2> <float3> <float4> |
Same <float> specifications as PSD_VOL model. This model is allowed for all media types except POROUS_BRINKMAN (cf. Media Type card). |
PSD_SEXP <float1> <float2> <float3> <float4> |
Same <float> specifications as PSD_VOL model. This model is allowed for all media types except POROUS_BRINKMAN (cf. Media Type card). |
SOLIDIFICATION <float1> |
Used to phase in a porous flow term in the liquid momentum equations for low volume fraction packing of particles in the Brinkman porous flow formulation (see discussion below). Used for Phillip’s model of suspensions for the Liquid Constitutive Equation, viz. CARREAU_SUSPENSION, SUSPENSION, FILLED_EPOXY or POWER_LAW_SUSPENSION.
This model is ONLY allowed for media type POROUS_BRINKMAN (cf. Media Type card). The functional form is: where μ0 is the clear fluid viscosity, φpart is the volume fraction of particles, or concentration divided by the maximum packing (0.68 for monodisperse spheres), and havg is the average element size. |
KOZENY_CARMAN <float1> <float2> |
The Kozeny-Carman equation relates the permeability to the porosity for a porous medium and has been shown to fit well the experimental results in many cases. This. equation is easily derivable from the PSD_* models for the case of uniform pore-size distribution, viz. a delta distribution (cf. Cairncross, et. al., 1996 for derivation). The model is currently implemented in the isotropic media case and is useful for deformable problems in which the porosity changes with deformation (cf. Porosity card DEFORM model). The functional form for this model is as follows: Here φ is the porosity, c0 is a constant consisting of tortuosity and shape factor of the pores, and Sv is the surface area per solid volume. The float parameters are:
|
EXTERNAL_FIELD <float1> |
This model reads in an array of values for the porosity from an initial exodus file. This allows for spatial variations in the parameter value.
The ExodusII field variable name should be “PERM”, viz. External Field = PERM Q1 name.exoII (see this card) |
Examples¶
Following is a sample card:
Permeability = CONSTANT 0.001
This specification leads to a constant permeability of 0.001.
Technical Discussion¶
For all models, this card provides the permeability, in units of [L2]. For saturated porous materials (viz. POROUS_BRINKMAN or POROUS_SATURATED media types), the viscosity from the Viscosity card is used to compute the porous conductivity, viz., permeability divided by viscosity. For unsaturated media types, the viscosity factor comes through the relative permeability cards (see Rel Gas Permeability and Rel Liq Permeability cards). Please consult the references below for the proper form of the equations.
The PSD_VOL (Probability Size Distribution, PSD) model treats the medium as a bundle of capillary tubes with a distribution of pores such that over a range of porek sizes the volume of pores is evenly distributed. For such a model, the maximum poresize varies with the porosity:
Then, the permeability is a function of the maximum pore-size and the pore-size distribution:
The input parameters for the PSD models are φ0, rmax(φ0), α, and 1 ⁄ τ2. More detail on the deformable porous medium models is given in Cairncross, et. al., 1996. The PSD_WEXP and PSD_SEXP are similar pore-size distribution models to PSD_VOL. The references below should be consulted for details on how to use these models.
References¶
GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk
GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk
SAND96-2149: Drying in Deformable Partially-Saturated Porous Media: Sol-Gel Coatings, Cairncross, R. A., P. R. Schunk, K. S. Chen, S. S. Prakash, J. Samuel, A. J. Hurd and C. Brinker (September 1996)
Liquid phase compressibility¶
Permeability = {model_name} {float_list} [L2]
Description / Usage¶
This card specifies the model and model parameters for liquid-phase compressibility, and was specifically designed for use in porous-media flow problems that are partially saturated (viz. Media Type card values of POROUS_UNSATURATED or POROUS_TWO_PHASE). This feature was added partially for numerical convenience in rigid porous media to accommodate regimes where the saturation level is at or near unity; at these saturation levels the capacitance term (see Technical Discussion below) all but vanishes, viz. there is no sensitivity of the saturation level to liquid phase pressure, and the mathematical behavior can change type. This occurs in situations of low permeability, narrow pore-size distribution, and sudden pressure spikes during simulation startup.
CONSTANT |
Name of the model for the compressibility coefficient, currently the only option. It requires a single parameter:
|
This card requires a companion card Liquid phase reference pressure.
Examples¶
The cards (using APREPRO variables)
Liquid phase compressibility = CONSTANT {beta_liquid}
Liquid phase reference pressure = CONSTANT {p_not}
leads to the application of a linearized compressibility model for the density of liquid in the time-derivative capacitance term. This is useful for rigid porous media when the conditions are such that the saturation front is sharp.
Technical Discussion¶
For Cls the most part, we have needed the Liquid Phase Compressibility capability to ease the startup of impregnation problems, in which an external pressure load is impulsively applied to a liquid layer being forced into a rigid porous matrix. The capacitance term as the saturation level approaches 1.0 (S->1) in the porous Darcy flow equation appears in Goma as
Here is the liquid solvent concentration (in both gas and liquid phases), φ is the porosity, ρls and is the liquid phase density. Here we employ the linearized density model:
where βls is the coefficient of compressibility entered on this card, viz. dρls ⁄ dPliq defined above, p0liq is the reference liquid pressure (see Liquid phase reference pressure* card)
FAQs¶
The following troubleshooting tips regarding startup of partially saturated porous media problems are part of the authors experience presented in Schunk, 2002 (GT- 009.3):
-Linear elements, viz. Q1 elements, are better for saturation front startup at an external boundary if the difference between the boundary specified liquid-phase pressure and the medium-initialized liquid phase pressure are drastically different. Quadratic elements in this case can lead to zero or low Saturation values at all computational Gaussian integration points and the front may never penetrate.
-Time stepping is all important. There are three relevant parameters: time-step scheme, initial time step size, and time-step error factor. The rules of thumb that can be established are as follows:
If you are using Porous Mass Lumping, you must set the Time Step Parameter to 0.0, or your performance will suffer. In fact, it is always a good idea in steep penetration front problems to use backward Euler techniques.
With mass lumping and first order time integration, you must control your step size with the tolerance setting. Too big of time step early on can propagate to large errors at later times when time stepping. You may need to experiment with the error tolerance on the Time step error card. Constantly scrutinize your results for correctness and suspect an error growth here.
You must have a significant capacitance term on the first time step. If your capacitance term is small, then the problem is elliptic and will try to satisfy all boundary conditions, and this can mess up your penetration front.You can use Liquid phase compressibility property to help this for steep front startup.
Are you getting stagnant calculations with time-step decreases but not change in iteration history? Problem is that you have lost your capacitance term. Compressibility of the liquid is sometimes a remedy, but also a more accurate predictor. Mass lumping can help too and accomplishes the same thing. Sometimes your initial time step can be too small for a good start. Try increasing it …
-Another startup issue: Steep discontinuities at boundaries and internally for initial conditions are bad, obviously. If your time step is such that the front cannot penetrate beyond one element in one time step, then with linear elements the capacitance term is ineffective (small) upon reduced time steps. Somehow you have got to get the front beyond one or two elements before things work properly. I find that ramping up the initial boundary conditions helps. Sometimes a large first time step to kick it is good too.
-On startup of a pressurized column of liquid penetrating into a porous substrate, I noticed that at zero-based p_liq, there was no problem elevating the applied pressure on the penetration, but at Atm-based p_liq we couldn’t start the problem without severe compressibility. However, compressibility affects the solution, and in fact allows you to push all of your column of liquid into a compressed layer in the substrate, with no Sat from propagation. So beware of poorly defined compressibility of liquid. Also, refinement in the porous layer helped the startup. But the most significant thing for the problem I was solving, don’t be surprised if just a little perturbation on externally applied pressure greatly affects the penetration rate. In fact, in one problem simply changing from p_ext of 1.01325e+6 to 1.11325+6 increases the penetration rate 2-fold initially. The steeper curves are harder to handle.
References¶
GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk
GT-009.3: GOMA’s capabilities for partially saturated flow in porous media, September 1, 2002, P. R. Schunk
Liquid phase reference pressure¶
Liquid phase reference pressure = CONSTANT <float> [M/L-t2] or [N/L2]
Description / Usage¶
This card is used to specify the model and model parameters for the liquid-phase compressibility reference pressure. See Liquid phase compressibility card for discussion and theory.
CONSTANT |
model for the reference pressure, currently the only available option. It requires a single floating point value:
|
Examples¶
The cards
Liquid phase compressibility = CONSTANT {beta_liquid}
Liquid phase reference pressure = CONSTANT {p_not}
leads to the application of a linearized compressibility model for the density of liquid in the time-derivative capacitance term. This is useful for rigid porous media when the conditions are such that the saturation front is sharp.
Technical Discussion¶
See discussion on Liquid phase compressibility card.
References¶
GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk
GT-009.3: GOMA’s capabilities for partially saturated flow in porous media, September 1, 2002, P. R. Schunk
Flowing Liquid Viscosity¶
FlowingLiquid Viscosity = CONSTANT <float> [M/Lt]
Description / Usage¶
This card is used to specify the model for the viscosity of liquid flowing through pores with the Brinkman model of flow through porous media, viz. see Media Type card with POROUS_BRINKMAN option. In the Brinkman model, the viscosity input through the Viscosity card is used as the Brinkman viscosity, and the viscosity input through this card is used in determining the hydraulic resistance. Detailed discussion of these two viscosities can be found by consulting the references below.
Definitions of the input parameters are as follows:
CONSTANT |
Name for the constant viscosity model.
|
Examples¶
Following is a sample card:
Flowing Liquid Viscosity = CONSTANT 101.0
This card is only applicable to the POROUS_BRINKMAN media type and results in a hydraulic resistance viscosity of 101.0.
Technical Discussion¶
See references below for discussion on use of this card.
References¶
GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk
Gartling, D. K., C. E. Hickox and R. C. Givler 1996. “Simulations of Coupled Viscous and Porous Flow Problems”, Comp. Fluid Dynamics, 7, 23-48.
Inertia Coefficient¶
Inertia Coefficient = CONSTANT <float> []
Description / Usage¶
This card is used to specify the model for the inertia coefficient cˆ in the Brinkman formulation for flow through porous media, viz. see POROUS_BRINKMAN option on Media Type card. Detailed discussion of this coefficient can be found by consulting the references below. Definitions of the input parameters are as follows:
CONSTANT |
Name of the model for the inertia coefficient.
|
Examples¶
Following is a sample input card that produces a weighting coefficient of 1.0 on the inertial term in the POROUS_BRINKMAN equations.
Inertia Coefficient= CONSTANT 1.0
Technical Discussion¶
See references below for discussion on use of this card.
References¶
GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk
Gartling, D. K., C. E. Hickox and R. C. Givler 1996. “Simulations of Coupled Viscous and Porous Flow Problems”, Comp. Fluid Dynamics, 7, 23-48.
Capillary Network Stress¶
Capillary Network Stress = {model_name}
Description / Usage¶
This card specifies the mechanism by which capillary stress and capillary pressure in the liquid phase of a partially saturated porous medium is transferred to the solid network. This model is active only when the porous_deform equation (see EQ card) is active, and the drained network is deformable under liquid phase pressure. The principles of this card rest in the theory of the effective stress principle. In effect, the model specified here can be used to change the affinity of the pore liquid to the solid network (more discussion below). The input parameter is the model for capillary network stress.
The options for {model_name} are the names of transfer mechanisms:
WETTING |
specifies that the porous skeleton has the same hydrostatic pressure as the liquid. This model has not been tested recently. See discussion below. |
PARTIALLY_WETTING |
specifies that the porous skeleton has a hydrostatic pressure that is the average of the liquid and gas phase pressures, weighted by their saturations (see related report on drying of deformable porous media by Cairncross, et. al., 1996). |
COMPRESSIBLE |
functions the same as the PARTIALLY_WETTING option but includes a factor that accounts for the compressibility of the solid material, viz. the actual struts of the solid material, not the network (see Cairncross, et. al., 1996). |
Technical Discussion¶
Basically, this card sets the functional form of the capillary stress contribution to the composite effective stress in a porous medium. The constitutive equation is as follows:
where ˜network is the drained network stress that would result in the absence of any pore fluid (gas or liquid). The function F depends on the model type specified on this card. For POROUS_SATURATED media types, this card is not used and F = pliq. For POROUS_UNSATURATED and POROUS_TWO_PHASE media types, F is as follows for different transfer mechanisms:
WETTING: The assumption here is that a thin liquid layer covers all surfaces.
PARTIALLY_WETTING: The most commonly used model.
COMPRESSIBLE: If the solid struts are also significantly compressible, viz. the solid bulk modulus Ks is of the same order of magnitude as the network skeleton bulk modulus, Kn, this model should be used. Not recently tested; please consult with Developers before using this option. PRS (6/13/2002)
References¶
SAND96-2149: Drying in Deformable Partially-Saturated Porous Media: Sol-Gel Coatings, Cairncross, R. A., P. R. Schunk, K. S. Chen, S. S. Prakash, J. Samuel, A. J. Hurd and C. Brinker (September 1996)
Rel Gas Permeability¶
Rel Gas Permeability = {model_name} <float> []
Description / Usage¶
This card specifies the model for the relative gas phase permeability for flow in a partially saturated porous media, such that the gas flow is the pressure gradient in the gas times the permeability times the relative gas phase permeability divided by the gas viscosity. This card rests on a consistency in the specification of the relative liquid permeability (see models on the Rel Liq Permeability card) and this, the relative gas permeability. Definitions of the input parameters are as follows:
CONSTANT |
{model_name} for constant relative gas phase permeability with a single input value:
|
The CONSTANT model is rarely used, as it is dependent on the saturation level and the relative liquid permeability value. Please see the Rel Liq Permeability card.
SUM_TO_ONE |
{model_name} for the relative gas phase permeability. This model assumes that the relative liquid permeability and relative gas permeability add to one.
|
Examples¶
Following is a sample card:
Rel Gas Permeability = SUM_TO_ONE 0.0001
This card specifies that the relative gas permeability in Darcy’s law for the gas flux is to depend on the liquid phase relative permeability such that the two sum-to-one. The gas viscosity here is specified to be 0.0001, in the appropriate viscosity units of M/L/t.
Technical Discussion¶
This card is only required for Media Type POROUS_TWO_PHASE. Darcy’s law for gas flow is, in its simplest form:
where, the Darcy velocity is proportional to the gradient in gas pressure, with k being the permeability, krelg being the relative gas permeability and μgas the viscosity of the gas. For the SUM_TO_ONE option above, the floating point constant is the gas phase viscosity, and the gas-phase relative permeability is calculated using
For the CONSTANT option the floating point constant must include the effect of viscosity, viz. the constant represents krelg/μgas
References¶
GT-009.3: GOMA’s capabilities for partially saturated flow in porous media, September 1, 2002, P. R. Schunk
SAND96-2149: Drying in Deformable Partially-Saturated Porous Media: Sol-Gel Coatings, Cairncross, R. A., P. R. Schunk, K. S. Chen, S. S. Prakash, J. Samuel, A. J. Hurd and C. Brinker (September 1996)
Rel Liq Permeability¶
Rel Liq Permeability = {model_name} {float_list} []
Description / Usage¶
This card is required for Media Type POROUS_TWO_PHASE. This card specifies the model for the relative liquid phase permeability for flow in a partially saturated porous media, such that the liquid flow is the pressure gradient in the liquid times the permeability times the relative liquid phase permeability divided by the liquid viscosity. Definitions of the input parameters are as follows:
{model_name} |
Name of the model for the relative gas phase permeability; the permissible values are CONSTANT, VAN_GENUCHTEN, PSD_VOL, PSD_WEXP, and PSD_SEX. |
{float_list} |
One or more floating point numbers (<float1> through <floatn>) whose values are determined by the selection for {model_name}. |
Permeability model choices and their parameters are discussed below.
CONSTANT <float1> |
a constant relative liquid permeability; this is a rarelyused option.
|
VAN_GENUCHTEN <float1> <float2> <float3> <float4> |
assumes that the relative liquid permeability is a function of the saturation (as specified in the Saturation card). The {float_list} contains four values for this model, where:
|
PSD_VOL <float1> |
This model can only be used in conjunction with the same model for permeability and saturation; a single input value isrequired:
All other parameters are loaded up from the Saturation and Permeability cards. |
PSD_WEXP <float1> |
This model can only be used in conjunction with the same model for permeability and saturation; a single input value is required:
|
PSD_SEXP <float1> |
This model can only be used in conjunction with the same model for permeability and saturation; a single input value is required:
|
Technical Discussion¶
The most often used model is that of VAN_GENUCHTEN. The functional form of this model is as follows:
where
and is the viscosity. This function is clipped to zero as and clipped to one as Seff → 1. PSD_* model theory details can be found in the references cited below. These models bring in more explicit dependence on pore size and size distribution, as well as other microstructural features. In the VAN_GENUCHTEN model, such parameter effects are embodied in the Saturation dependence, which is empirically fit through the saturation function.
References¶
GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk
GT-009.3: GOMA’s capabilities for partially saturated flow in porous media, September 1, 2002, P. R. Schunk
SAND96-2149: Drying in Deformable Partially-Saturated Porous Media: Sol-Gel Coatings, Cairncross, R. A., P. R. Schunk, K. S. Chen, S. S. Prakash, J. Samuel, A. J. Hurd and C. Brinker (September 1996)
Saturation¶
Saturation = {model_name} {float_list} []
Description / Usage¶
This card specifies the model for the liquid saturation in a partially saturated porous media, which is frequently observed experimentally to be a function of the capillary pressure (gas pressure minus liquid pressure). This card is required for Media Type specifications of POROUS_PART_SAT, POROUS_UNSAT, and POROUS_TWO_PHASE. Definitions of the input parameters are as follows:
{model_name} |
Name of the model for the liquid in a partially saturated porous media. The permissible values are CONSTANT,VAN_GENUCHTEN, TANH, PSD_VOL, PSD_WEXP, and PSD_SEXP. |
{float_list} |
One or more floating point numbers (<float1> through <floatn>) whose values are determined by the selection for {model_name}. |
Saturation model choices and their parameters are discussed below.
CONSTANT <float1> |
For the constant value of saturation model. This model is rarely used, unless one wanted to study the flow of gas and liquid at some constant, pre-specified saturation as a function of gas and liquid phase pressure. |
VAN_GENUCHTEN |
The VAN_GENUCHTEN model assumes that saturation is a function of the capillary pressure. The {float_list} contains four values, where:
|
TANH <float_list> |
The first version of the TANH model assumes that saturation is only a function of capillary pressure. The {float_list} contains four values, where:
|
PSD_VOL <float1> <float2> |
This model can only be used in conjunction with the same model for permeability and relative liquid permeability; two input values are required:
|
PSD_WEXP <float1> <float2> |
This model can only be used in conjunction with the same model for permeability and relative liquid permeability; two input values are required:
|
PSD_SEXP <float1> <float2> |
This model can only be used in conjunction with the same model for permeability and relative liquid permeability; two input values are required:
|
Examples¶
Following is a sample card:
Saturation = VAN_GENUCHTEN 0.01 0.01 3.9 1.
The parameters on this VAN_GENUCHTEN specification are basically curve fit parameters to experimental measured saturation values versus capillary pressure. They do have some physical meaning, as is described below, and in the references.
Technical Discussion¶
The saturation function specification is perhaps the most critical and most influential function for capturing accurate behavior of flow through partially saturated porous media. The basic cap of this function versus capillary pressure is depicted in the figure below: Notice the plateau of saturation at unity at low capillary pressures (high positive liquid pressures) and the dip to the irreducible water saturation at high capillary pressures. In most real operations, this dependence will be highly sensitive to many factors: viz. whether you are filling or vacating the pore space, whether network stress in poroelastic problems is leading to liquid tension, etc.
The Van Genuchten model has the following functional form:
Here the irreducible water saturation is θw, the irreducible air saturation 0air, the suction factor is α, and the exponents β and m, the latter of which is 1 – 1 ⁄ β.
The TANH model has the following functional form:
where a and b are automatically calculated from
and c and d are two fitted coefficients provided as input parameters. Here the irreducible water saturation is 0w, the irreducible air saturation 0air, and are also provided by the user as input parameters. Pc is the capillary pressure which has a lower limit of 1.E-5.
References¶
GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk.
GTM-029.0: SUPG Formulation for the Porous Flow Equations in Goma, H. K. Moffat, August 2001 (DRAFT).
SAND96-2149: Drying in Deformable Partially-Saturated Porous Media: Sol-Gel Coatings, Cairncross, R. A., P. R. Schunk, K. S. Chen, S. S. Prakash, J. Samuel, A. J. Hurd and C. Brinker (September 1996).
Porous Weight Function¶
Porous Weight Function = {GALERKIN | SUPG} <float>
Description / Usage¶
This required card is used to specify the weight function form on the capacitance term of the Darcy flow equations for partially saturated flow (viz. for Media Type specifications of POROUS_PART_SAT and POROUS_UNSAT, and POROUS_TWO_PHASE.) The standard approach is to use a Galerkin formulation, but often times the SUPG option allows for a more stable time integration algorithm using the classic Streamwise Upwinding Petrov Galerkin weight function (see references below). The model options for this card are as follows:
GALERKIN |
Name of the weight function formulation. This option requests a standard Galerkin finite element weighted residual treatment. A parameter is required, viz. <float>, but it is not used by Goma; it should be set to zero.
|
SUGP |
Name of the weight function formulation. This option requests a streamwise upwinding Petrov-Galerkin formulation. A floating point parameter is required as a SUPG weighting parameter and it should be set between 0.0 (for no upwinding) and 1.0 (for full upwinding).
|
The default model if this card is missing is GALERKIN.
Technical Discussion¶
As mentioned above, this card is used to invoke a streamwise upwinding scheme for purposes of stabilizing the solution around steep saturation fronts. Galerkin finite element treatment is often an extremely inaccurate discretization for propagating a discontinuity, such as is the case around these fronts, and often has to be supplemented with streamwise diffusion and/or mass lumping so that the saturation variable remains monotonic and well behaved, viz. to keep it from going below zero. Another expedient to aid in keeping the front smooth and monotonic is to use mass lumping (cf. Mass Lumping card).
References¶
GTM-029.0: SUPG Formulation for the Porous Flow Equations in Goma, H. K. Moffat, August 2001 (DRAFT).
Bradford, S. F. and N. D. Katopodes, “The anti-dissipative, non-monotone behavior of Petrov-Galerkin Upwinding,” International J. for Numerical Methods in Fluids, v. 33, 583-608 (2000).
Brooks, A. N. and T. J. R. Hughes, “Streamline Upwind/Petrov-Galerkin Formulations for Convection Dominated Flows with Particular Emphasis on the Incompressible Navier-Stokes Equations,” Comp. Math. In Appl. Mechanics and Eng., 32, 199 - 259 (1992).
Gundersen, E. and H. P. Langtangen, “Finite Element Methods for Two-Phase Flow in Heterogeneous Porous Media,” in Numerical Methods and Software Tools in Industrial Mathematics, Morten Daehlen, Aslak Tveito, Eds., Birkhauser, Boston, 1997.
Helmig, R. and R. Huber, “Comparison of Galerkin-type discretization techniques for two-phase flow in heterogeneous porous media,” Advances in Water Resources, 21, 697-711 (1998).
Unger, A. J. A., P. A. Forsyth and E. A. Sudicky, “Variable spatial and temporal weighting schemes for use in multi-phase compositional problems,” Advances in Water Resources, 19, 1 - 27 (1996).
Porous Mass Lumping¶
Porous Mass Lumping = {yes | true | no | false}
Description / Usage¶
Mass lumping is a technique for handling stiff problems with propagation of discontinuities. By “Mass” we mean the so-called mass matrix, or the submatrix generated by the time-derivative term in the physical equations. Discretization of this term with the standard Galerkin finite element method produces a symmetric, but nondiagonal matrix, also known as the consistent mass matrix as it adheres to the proper weak form. This required card specifies the mode in which the mass matrix is computed. If mass lumping is turned on, then the matrix is formed on a nodal, collocated basis and the mass matrix becomes diagonal. This technique expedites timeintegration during the propagation of steep fronts.
The mass lumping here applies ONLY to the time-derivative term in the EQ=porous_liq or EQ=porous_gas equations in Goma, and only when the Media Type is either POROUS_UNSATURATED or POROUS_TWO_PHASE. Mass lumping is not enabled for saturated porous flow. Please see technical discussion below for other usage tips. The card options are as follows:
yes | true Compute mass matrix with the lumped approach.
no | false Compute mass matrix with the standard Galerkin approach. This is the default.
Examples¶
Porous Mass Lumping = true
Technical Discussion¶
Mass lumping is almost essential for unsaturated porous flow problems, especially at low permeabilities and in conditions for which the saturation front is sharp. It is recommended that mass lumping always be used for all unsaturated porous flow problems. However, with such use it is also recommended to use ONLY 1st order time integration (see Time step parameter card and choose Backward-Euler, 0.0). For second order time integration on the porous flow equations, mass lumping does not provide any benefit as the increased accuracy in time tends to lead to insufficient accuracy in space, and wiggles form.
Mass lumping is not currently available for saturated deformable porous flow.
References¶
GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk
GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk
GTM-029.0: SUPG Formulation for the Porous Flow Equations in Goma, H. K. Moffat, August 2001 (DRAFT).
Bradford, S. F. and N. D. Katopodes, “The anti-dissipative, non-monotone behavior of Petrov-Galerkin Upwinding,” International J. for Numerical Methods in Fluids, v. 33, 583-608 (2000).
Gundersen, E. and H. P. Langtangen, “Finite Element Methods for Two-Phase Flow in Heterogeneous Porous Media,” in Numerical Methods and Software Tools in Industrial Mathematics, Morten Daehlen, Aslak Tveito, Eds., Birkhauser, Boston, 1997.
Helmig, R. and R. Huber, “Comparison of Galerkin-type discretization techniques for two-phase flow in heterogeneous porous media,” Advances in Water Resources, 21, 697-711 (1998).
Unger, A. J. A., P. A. Forsyth and E. A. Sudicky, “Variable spatial and temporal weighting schemes for use in multi-phase compositional problems,” Advances in Water Resources, 19, 1 - 27 (1996).
Porous Diffusion Constitutive Equation¶
Porous Diffusion Constitutive Equation = {model_name}
Description / Usage¶
This required card is used to specify the species diffusion model for the gas phase in a porous medium. Just now there is only one option, but plans are to expand the options to include multicomponent diffusion models (cf. Diffusion Constitutive Equation card). It is important to note that this model specification only applies to the gas phase of each component. Liquid phase species diffusive transport has not been implemented as of 12/19/01.
Definitions of the input parameters are as follows, with only a single permissible value:
DARCY_FICKIAN |
Name of the model for the diffusion constitutive equation in the porous gas phase. |
This model simply implies that gas species can be transported relative to the solid skeleton phase not only by a pressure gradient, as in Darcy’s law, but also by Fickian diffusion.
Examples¶
The following sample input card uses the APREPRO variable model_name (which is set to DARCY_FICKIAN.
Porous Diffusion Constitutive Equation = {model_name}
Technical Discussion¶
Currently, the DARCY_FICKIAN model is the only option for the porous diffusion equation and it only applies to one phase. When this card is parsed, it is contained in a solvent species loop. When we allow more than one volatile species, we will eventually allow for other diffusion constitutive equation models, e.g. of the Stefan-Maxwell type. Also, we will have to build a phase dependence into this card, as the diffusion law may be different in the liquid and in the gas. Right now, we do not allow for diffusion transport (viz. by a chemical potential or concentration gradient) in the liquid phase of a porous medium. Please consult references below for theoretical discussion.
References¶
GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk
GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk
SAND96-2149: Drying in Deformable Partially-Saturated Porous Media: Sol-Gel Coatings, Cairncross, R. A., P. R. Schunk, K. S. Chen, S. S. Prakash, J. Samuel, A. J. Hurd and C. Brinker (September 1996)
Porous Gas Diffusivity¶
Porous Gas Diffusivity = {model_name} <integer> <float_list> [L2/t]
Description / Usage¶
This card sets the model for the porous gas diffusivity, or the diffusion coefficient for diffusive species flux in the gas phase of a porous medium. It is applicable to media types POROUS_UNSATURATED and POROUS_TWO_PHASE (see Media Type card).
Definitions of the input options for {model_name} and the <integer> and <float> parameters fro each model are as follows:
CONSTANT <integer> <float1> |
the name for the constant diffusivity model.
|
POROUS <integer> <float1> <float2> <float3> <float4> <float5> |
the name for a microstructure dependent porous medium model.
|
For two-phase or unsaturated flow in a porous medium, the diffusivity calculated by this model is the diffusivity of solvent vapor through the gas phase in the pore-space (see Martinez, 1995).
Examples¶
Porous Gas Diffusivity = POROUS 0 1.e-5 0.5 1.e+6 25.0 3
See the equation below for the diffusivity model that this card represents.
Technical Discussion¶
The generalized flux of liquid phase solvent, in both gas and liquid phases, contains a term that accounts for diffusion of the liquid solvent species as gas vapor (see references below). That flux is as follows:
If the media type is POROUS_TWO_PHASE, this expression is divided by
and if in addition it is temperature dependent, this expression is multiplied by
References¶
GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk
GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk
SAND94-0379: “Formulation and Numerical Analysis of Nonisothermal Multiphase Flow in Porous Media”, Sandia Technical Report, Martinez, M. J., 1995
SAND96-2149: Drying in Deformable Partially-Saturated Porous Media: Sol-Gel Coatings, Cairncross, R. A., P. R. Schunk, K. S. Chen, S. S. Prakash, J. Samuel, A. J. Hurd and C. Brinker (September 1996)
Porous Latent Heat Vaporization¶
Porous Latent Heat Vaporization = CONSTANT <integer> <float> [E/M]
Description / Usage¶
This required card is used to specify the model for the latent heat of vaporization for each liquid solvent species in a partially saturated porous media flow problem, viz. Media Type card set to POROUS_UNSATURATED or POROUS_TWO_PHASE. As of 6/13/2002, we only allow single liquid phase solvent, and the porous enthalpy equation is being tested. Definitions of the input parameters are as follows:
CONSTANT |
Name of the constant latent heat of vaporization model.
|
Examples¶
The following is a sample input card:
Porous Latent Heat Vaporization = CONSTANT 0 1000.2
See the equation below for the diffusivity model that this card represents.
Technical Discussion¶
First order phase change involves the adsorption or expulsion of heat. This thermal effect is modeled through the porous energy equation (see EQ cards; this equation was under development and testing as this manual was being assembled) with a source term that depends on the evaporation/condensation rate.
References¶
No References.
Porous Latent Heat Fusion¶
Porous Latent Heat Fusion = CONSTANT <integer> <float> [E/M]
Description / Usage¶
This required card is used to specify the model for the latent heat of fusion (or freezing) for each liquid solvent species in a partially saturated porous media flow problem, viz. Media Type card set to POROUS_UNSATURATED or POROUS_TWO_PHASE. As of 6/13/2002, we only allow single liquid phase solvent and the porous enthalpy equation is being tested. Definitions of the input parameters are as follows:
CONSTANT |
Name of the constant latent heat of fusion model.
|
Examples¶
The following is a sample input card:
Porous Latent Heat Fusion = CONSTANT 0 1000.2
See the equation below for the diffusivity model that this card represents.
Technical Discussion¶
First order phase change involves the adsorption or expulsion of heat. This thermal effect is modeled through the porous energy equation (see EQ cards; this equation was under development and testing as this manual was being assembled) with a source term that depends on the evaporation/condensation rate. Fusion implies a liquid to solid transition. It is envisioned that this card will someday be used for porous flow in mushy zones of solidifying metals, or the freezing of water in a porous solid.
References¶
No References.
Porous Vapor Pressure¶
Porous Vapor Pressure = {model_name} {integer} {float_list} [M/L-t2]
Description / Usage¶
Used to specify the model for the vapor pressure for each multiphase flow component in the porous medium that is activated for Media Type POROUS_UNSATURATED or POROUS_TWO_PHASE.
Definitions of the input parameters are as follows:
{model_name} |
The permissible values for the model in this class are KELVIN and FLAT for a volatile liquid, and NON_VOLATILE for a non-volatile liquid. |
{integer} |
All models require an integer field after the model name which is the species_number; always set to zero until a multicomponent capability exists. |
{float_list} |
One or more floating point numbers (<float1> through <floatn>) whose values are determined by the selection for {model_name}. |
Porous vapor pressure model choices and their parameters are presented below; consult the Technical Discussion for relevant details.
KELVIN <integer> <float1> <float2>… <float5> |
For the KELVIN porous vapor pressure model, the {float_list} has a five values:
|
FLAT <integer> <float1> <float2>… <float5> |
For the FLAT porous vapor pressure model, the {float_list} has a five values (same as KELVIN above):
The FLAT option requires the same parameters as the KELVIN model but leaves out the exponential function. |
NON_VOLATILE <integer> |
The NON_VOLATILE model requires no additional input. |
Examples¶
The sample input card:
Porous Vapor Pressure = FLAT 0 {Vap_Pres} {density} {30.} {Rgas} {T}
applies the FLAT model as described above to vapor-liquid equilibrium (assumed to be single component for now) using all APREPRO-defined parameters.
Technical Discussion¶
The KELVIN option is used to include the effect of vapor-pressure lowering that results in equilibrium over high curvature menisci, i.e., small pores. The equation form of this is:
The FLAT option requires the same parameters but leaves out the exponential function. The constants are still needed so that the gas-phase concentration can be calculated with the ideal gas law. The functional form is
where S is the local saturation, and ρgv is the gas phase density of vapor. This model is ad-hoc but nonetheless leads to some interesting results. It basically says that as saturation increases, the gas-liquid menisci, and correspondingly the interfacial area available for evaporation, become more concentrated and hence the gas-phase vapor concentration increases.
The NON_VOLATILE option should be set if no gas-phase transport of vapor of the liquid phase component is desired, as if the liquid phase were non-volatile. Goma, with this choice, sets the gas phase concentration of liquid vapor to zero.
For nonvolatile pore liquids, the vapor pressure on a flat interface, viz. the first required floating point on this card, should be set to zero. As of 6/13/02 this card has only been implemented for pure liquid solvents, so that no equilibrium solvent partitioning across the interface is present.
FAQs¶
Sometimes system aborts can happen with the Kelvin model because of real large, negative capillary pressures. In this case, the exponential term can exceed the machine limit. This can happen well into a transient run. The user should be aware of this; consult GT-009.3 for tips related to dealing with this problem.
References¶
GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk
GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk
SAND96-2149: Drying in Deformable Partially-Saturated Porous Media: Sol-Gel Coatings, Cairncross, R. A., P. R. Schunk, K. S. Chen, S. S. Prakash, J. Samuel, A. J. Hurd and C. Brinker (September 1996)
Porous Liquid Volume Expansion¶
Not currently enabled (12/21/2001)
Description / Usage¶
This card is not currently activated.
Examples¶
No examples.
Technical Discussion¶
No Discussion.
References¶
No References.
Porous Gas Constants¶
Porous Gas Constants = IDEAL_GAS <float_list> [varies]
Description / Usage¶
This required card is used for Media Types of POROUS_UNSATURATED and POROUS_TWO_PHASE, and is used to input some standard thermodynamic gas constants needed for vapor-liquid equilibrium calculations (see Media Type card). Eventually more than one model may be allowed for nonideal gas situations.
The IDEAL_GAS model is the only model currently requiring standard constants; they are defined as follows:
IDEAL_GAS |
the model name requiring constants for the thermodynamic ideal gas law.
|
Technical Discussion¶
For POROUS_UNSATURATED media types the ambient pressure dictates the equilibrium pressure for the calculation of the gas-phase density of solvent (viz. the total ambient pressure minus the vapor pressure will be the gas partial pressure, from which the concentration of gas can be computed based on the other gas constants). In POROUS_TWO_PHASE media types, the gas partial pressure is a dependent variable and computed as a part of the Darcy law mass balance. In this case the dynamic pressure is used instead of <float4> here for the calculation of the gas-phase concentrations.
It is important to realize that setting the ambient pressure on this card for Media Types of POROUS_UNSATURATED will potentially affect your saturation curve and the appropriate values of your liquid phase pressure boundary conditions. If possible, you should set this value to zero, and base your Saturation versus vapor pressure curve accordingly. Also, in that case your liquid pressure boundary conditions can all be referenced to zero. However, if you choose a gauge pressure, or thermodynamic pressure, you Saturation/capillary pressure curve must be shifted accordingly, as do your boundary conditions. Also, remember these pressures will affect your solid pressure state in poroelastic problems.
References¶
GT-008.2: Porous Media Capabilities/Tutorial for GOMA. User Guidance for Saturated Porous Penetration Problems, August 11, 1999, P. R. Schunk
GT-009.3: GOMA’s Capabilities for Partially Saturated Flow in Porous Media, September 1, 2002, P. R. Schunk
SAND96-2149: Drying in Deformable Partially-Saturated Porous Media: Sol-Gel Coatings, Cairncross, R. A., P. R. Schunk, K. S. Chen, S. S. Prakash, J. Samuel, A. J. Hurd and C. Brinker (September 1996)