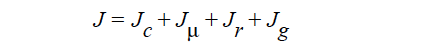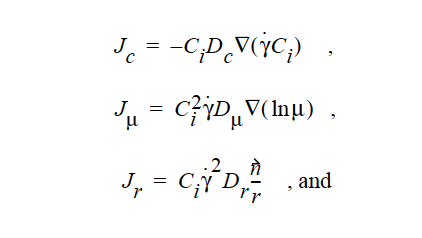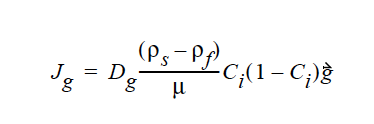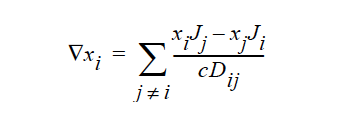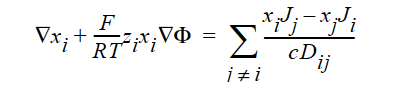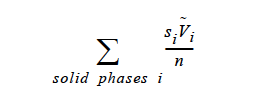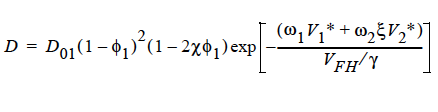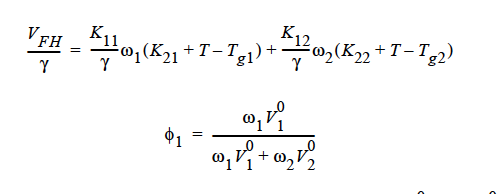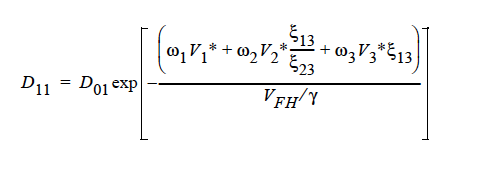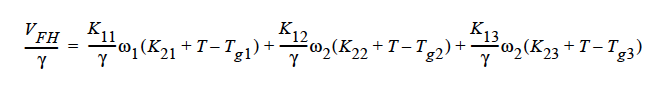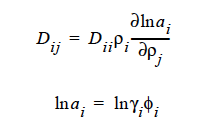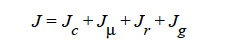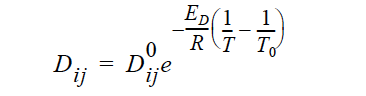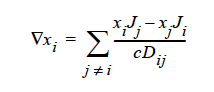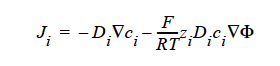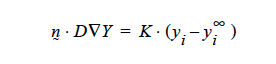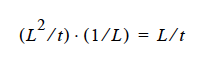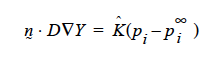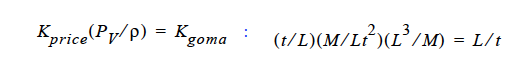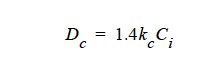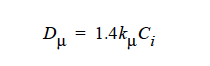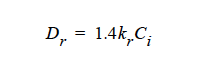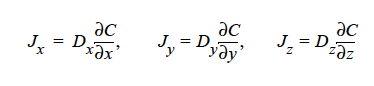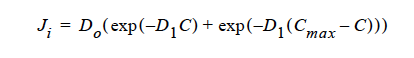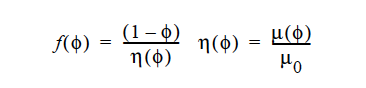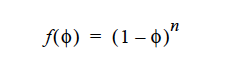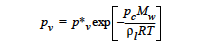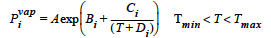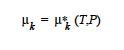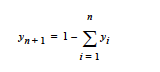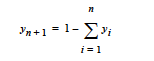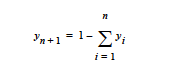Species Properties¶
The section of material properties defines the models and parameters governing diffusive mass transport, whether it be ordinary, forced or thermal diffusion of species. Included in those generalizations are electrical potential-driven species movements. Models include those for single species, especially particle-laden suspensions, binary species and multi-component systems. Models for various equations of mass transport are included, various models of diffusion properties, different representations of species by means of molar, mass or volume concentrations, various models of vapor pressure for multiphase flow and on material boundaries for lumped parameter analyses, and properties for charged species.
Number of Species¶
Number of Species =
Description / Usage¶
This card is no longer used. It may be removed from the Material file.
Examples¶
No Example.
Technical Discussion¶
The Number of Species is now determined by Goma from the Problem Specification for each material in the Goma input file.
References¶
No References.
Diffusion Constitutive Equation¶
Diffusion Constitutive Equation = {model_name}
Description / Usage¶
This card is used to specify the constitutive equation governing mass transport. Definitions of the input parameters are as follows:
{model_name} |
Name of the model for the diffusion constitutive equation. The currently supported options are:
|
This card requires only the specification of a {model_name}. The Technical Discussion subsection below presents each of these models.
Technical Discussion¶
NONE indicates that the material block to which this material file applies is a nondiffusing material. FICKIAN implies that the rate of diffusion is proportional to the gradient in volume fraction and the diffusion coefficient of each species. DARCY implies that mass transport occurs by pressure-driven flow through a porous medium. DARCY_FICKIAN implies that mass transport occurs by both diffusion and pressuredriven flow in a porous medium.
HYDRODYNAMIC implies that mass transport of at least one species is driven by gradients in the second invariant of the rate of deformation tensor (shear rate) and gradients in viscosity (Phillips, et.al. 1992). This model also includes a sedimentation flux term to account for the motion of non-neutrally buoyant particles resulting from gravitation (Zhang and Acrivos, 1994) and a curvature-driven flux term from the normal component of the acceleration vector (Krishnan et al., 1996). This model is used in predicting the particle distributions of particulate suspensions undergoing flow. For this model, the mass flux vector J is given by the following:
where
where Ci is the particulate phase volume fraction, i is the species number designation of the particulate phase, the shear rate, μ the viscosity, the normal unit acceleration vector, r the curvature of streamlines, Dc, Dμ, Dr and Dg the “diffusivity” parameters, ρs and ρf the particle and fluid phase densities, respectively, and , the gravitational acceleration vector.
GENERALIZED_FICKIAN is based on the generalized-Fick’s law (Taylor and Krishna, 1993). The mass transport of each species is influenced by all of the species in the mixture.
ρ is the mass-concentration of species. The elements along the diagonal, Dii, are selfdiffusivities, while Dij are mutual-diffusivities between species i and j. Note that mutual diffusivities in generalized formulation can be both positive and negative.
FICKIAN_CHARGED indicates a model for multicomponent transport (diffusion and migration) of charged species in dilute electrolyte solutions will be used. The Fickian diffusivity of species i, Di, as defined in the following Fickian flux model (cf. Newman 1991; Chen 2000)
is taken to be constant. Here, ci is molar concentration of species i, Φ is electrical potential in electrolyte solution, zi is charge number of species i, F is the Faraday constant (96487 C/mole), R is the universal gas constant (8.314 J/mole-K), and T the electrolyte solution temperature.
STEFAN-MAXWELL activates a model for multicomponent diffusion of neutral species in concentrated solutions. The Stefan-Maxwell diffusivities, Dij, as defined in the following Stefan-Maxwell flux model (cf. Chen et al. 2000, Chen et al. 1998):
are taken to be constant. Here, xi is mole fraction of species i, Ji the molar flux of species i, and c the total molar concentration. Since Dij = Dji and Dii are not defined, only n(n-1)/2 Stefan-Maxwell diffusivities are required (here, n is the total number of diffusing species). For example, for n = 3 (i.e., a solution having three species), three Stefan-Maxwell diffusivities are needed: D12, D13, and D23.
STEFAN-MAXWELL_CHARGED For multicomponent transport (diffusion and migration) of charged species in concentrated electrolyte solutions. The Stefan- Maxwell diffusivities, Dij, as defined in the following Stefan-Maxwell flux model (cf. Chen et al. 2000, Chen et al. 1998)
are taken to be constant, as in the case of multicomponent diffusion of neutral species in concentrated solutions. Here, the charged species definitions are the same as for the FICKIAN_CHARGED model.
References¶
GTM-025.0: Chen, K. S., “Modeling diffusion and migration transport of charged species in dilute electrolyte solutions: GOMA implementation and sample computed predictions from a case study of electroplating”, Sandia memorandum, September 21, 2000.
Chen, K. S., Evans, G. H., Larson, R. S., Noble, D. R., and Houf, W. G. “Final Report on LDRD Project: A Phenomenological Model for Multicomponent Transport with Simultaneous Electrochemical Reactions in Concentrated Solutions”, SAND2000- 0207, Sandia National Laboratories Technical Report (2000).
Chen, K. S., Evans, G. H., Larson, R. S., Coltrin, M. E., and Newman, J. “Multidimensional modeling of thermal batteries using the Stefan-Maxwell formulation and the finite-element method”, in Electrochemical Society Proceedings, Volume 98-15, p. 138-149 (1998).
Krishnan, G. P., S. Beimfohr, and D. Leighton, 1996. “Shear-induced radial segregation in bidisperse suspensions,” J. Fluid Mech. 321, 371
Newman, J. S., Electrochemical Systems, Prentice Hall, Inc., Englewood Cliffs, New Jersey (1991).
Phillips, R.J., R.C. Armstrong, and R.A. Brown, 1992, “A constitutive equation for concentrated suspensions that accounts for shear-induced particle migration,” Physics of Fluids A, 4(1), 30-40.
Taylor, R. and R. Krishna. 1993. Multicomponent Mass Transfer. John Wiley & Sons, New York.
Zhang K., and A. Acrivos, 1994, “Viscous resuspension in fully-developed laminar pipe flows,” Int. J. Multiphase Flow, (20)3, 579-591.
Species Weight Function¶
Species Weight Function = {model_name} <float>
Description / Usage¶
This optional card is used to specify the weight functions to be used on the weighted residual of the species convective diffusion equations. For high Peclet number cases, you may want to use a Petrov-Galerkin formulation rather than a Galerkin formulation.
{model_name} |
Name of the formulation model. Valid entries are GALERKIN, for a full Galerkin formulation, SUPG, for a streamwise upwinded Petrov-Galerkin formulation.
|
When this card is absent, the default {model_name} is GALERKIN.
Technical Discussion¶
No Discussion.
References¶
No References.
Number of Chemical Reactions¶
Number of chemical reactions = <integer>
Description / Usage¶
This card is used to specify the number of electrochemical reactions being modeled in an electrode (anode or cathode), as in a thermal-battery cell.
Technical Discussion¶
No Discussion.
References¶
No References.
Reaction Rate¶
Reaction Rate = <model_name> <float1> <float2>
Description / Usage¶
This card is used to specify rates of species electrochemical reactions in the anode and cathode regions in a LiSi/LiCl-KCl/FeS2 thermal battery cell using Butler-Volmer kinetics.
This property currently allows for a single {model_name} which has two parameters:
ELECTRODE_KINETICS |
the name of reaction rate model
|
Two companion cards, THERMODYNAMIC POTENTIAL and INTERFACIAL AREA are required to complete the specification of parameters present in the Butler-Volmer kinetic model of current density.
Examples¶
The following are two sample cards:
Reaction Rate = ELECTRODE_KINETICS 0.5 0.5
Reaction Rate = ELECTRODE_KINETICS 1.0 1.0
Technical Discussion¶
No Discussion.
References¶
No References.
Thermodynamic Potential¶
Thermodynamic Potential = {model_name} {float_list}
Description / Usage¶
This card is used to specify the anodic or cathodic thermodynamic potential in a thermal battery cell.
{model_name} |
Name of thermodynamic potential model. Currently, two thermodynamic potential models are available, namely LiSi and FeS2. Each of these and their accompanying input parameters (the <float_list>) is given below: |
LiSi |
This model requires seven floating-point parameters:
|
FeS2 |
This model requires eight floating-point parameters:
|
Examples¶
The following are two sample input cards:
Thermodynamic Potential = LiSi 0.283 0.474 0.088 0.275 54.61 0.0246 3.25
Thermodynamic Potential = FeS2 0.375 0.434 0.5 0.046 0.244 23.93 0.0246 4.0
Technical Discussion¶
No Discussion.
Interfacial Area¶
Interfacial Area = {model_name} {float_list}
Description / Usage¶
This card is used to specify the product of interfacial area per unit volume by exchange current density (i.e., ai0) in the Butler-Volmer kinetic model of current density.
{model_name} |
Name of the model for interfacial area, of which there are currently two available, namely CONSTANT and THERMAL_BATTERY. |
CONSTANT |
constant value of Interfacial Area
|
THERMAL_BATTERY |
this option requires the following nine parameters:
|
Examples¶
The following are two sample input cards:
Interfacial Area = CONSTANT 1.0
Interfacial Area = THERMAL_BATTERY 20.0 0.375 20000.0 846.0 0.046 0.244 23.93 0.0246 4.0
Technical Discussion¶
No Discussion.
References¶
No References.
Solution Temperature¶
Solution Temperature = {model_name} <float_list>
Description / Usage¶
This card is used to specify the temperature of an electrolyte solution (i.e., when diffusion and migration transport of charged species is involved).
{model_name} |
Name of the electrolyte-solution model, for which there are currently two options: CONSTANT and THERMAL_BATTERY; the former model has a single parameter in the <float_list> while the latter has six. |
CONSTANT |
A constant model of the solution temperature.
|
THERMAL_BATTERY |
A specialized model of electrolyte solutions for Thermal Batteries (Chen, et. al., 2000).
|
Examples¶
The following are two sample input cards:
Solution Temperature = CONSTANT 313.0
Solution Temperature = THERMAL_BATTERY 846. 298. 0.0316 7.7 0.6 1030.
Technical Discussion¶
No Discussion.
References¶
SAND2000-0207: Final Report on LDRD Project: A Phenomenological Model for Multicomponent Transport with Simultaneous Electrochemical Reactions in Concentrated Solutions, Chen, K. S., Evans, G. H., Larson, R. S., Noble, D. R., and Houf, W. G., January 2000.
Porosity¶
Porosity = {model_name} <float1> [float2]
Description / Usage¶
This card is used to specify the porosity model for the anode or separator or cathode region in a thermal battery cell.
Definitions of the {model_name} and the associated input parameters (<float>) are as follows:
CONSTANT |
the name of the porosity model.
|
THERMAL_BATTERY |
the name of the porosity model.
|
Examples¶
A sample input card for this material property might look like this:
Porosity = THERMAL_BATTERY 0.244 8.1185
Technical Discussion¶
This is a porosity model for a special application in which the model for the diffusion constitutive equation is STEFAN_MAXWELL_CHARGED, which enables modeling the transport of multiple charged species with simultaneous electrochemical reaction(s) in a concentrated solution, as in a thermal-battery cell.
See the reference below for a discussion of Thermal Battery modeling with Goma.
References¶
SAND2000-0207: Final Report on LDRD Project: A Phenomenological Model for Multicomponent Transport with Simultaneous Electrochemical Reactions in Concentrated Solutions, K. S. Chen, G. H. Evans, R. S. Larson, D. R. Noble and W. G. Houf, January 2000.
Diffusivity¶
Diffusivity = {model_name} <species> <float_list> [varies]
Description / Usage¶
This required card is used to specify the model for the diffusivity for each species. Definitions of the input parameters are as follows:
{model_name} |
Name of the diffusivity model. This parameter can have one of the following values:
|
<species> |
An integer designating the species equation. |
{float_list} |
the name of the porosity model. One or more floating point numbers (<float1> through <floatn> whose value is determined by the selection for {model_name}. Note that not all the models employ a {float_list}. |
Thus, choices for {model_name} and the accompanying input parameter list are dependent on the {model_name} selected for the Diffusion Constitutive Equation. In some cases, the above model choices have special definitions, while for others some of the above choices do not exist. Thus, the presentation below is keyed to the value chosen for the Diffusion Constitutive Equation model.
When the Diffusion Constitutive Equation model is set to NONE, meaning the material block to which this material file applies is a non-diffusing material, this Diffusivity card should be present in the Material file specification but the model and its parameters will not be used.
For the FICKIAN, GENERALIZED_FICKIAN, DARCY and DARCY_FICKIAN flux models, the following options are valid choices for the Diffusivity {model_name} and accompanying parameter lists.
CONSTANT <species> <float1> |
a constant diffusivity model
|
USER <species> <float_list> |
a user-defined model, the <species> is specified and the set of parameters <float1> through <floatn> is defined by the function usr_diffusivity in the file user_mp.c. |
POROUS <species> <float_list> |
a diffusivity that depends on the saturation and porosity in a porous medium. For two-phase or unsaturated flow in a porous medium, the diffusivity calculated by this model is the diffusivity of solvent vapor through the gas phase in the pore-space This model has been deprecated as the porous equation rewrite has proceeded; it is not recommended for use! |
GENERALIZED <species> <float1> <float2> |
For constant diffusivities used by generalized Fick’s law. The {float_list} consists of two values for each species i or i-j species pair:
|
FREE_VOL <species> <floatlist> |
For a diffusivity determined by free volume theory. The {float_list} for this model contains twelve values:
Note, this model can be run only with a single species equation, i.e., two components |
GENERALIZED_FREE_VOL <species> <floatlist> |
For constant diffusivities used by generalized Fick’s law. The {float_list} consists of two values for each species i or i-j species pair:
|
FREE_VOL <species> <floatlist> |
For a diffusivity determined by free volume theory. The {float_list} for this model contains twelve values:
Note, this model can be run only with a single species equation, i.e., two components |
GENERALIZED_FREE_VOL <species> <floatlist> |
a diffusivity model based on free volume theory and the generalized Fick’s law. This is similar to the FREE_VOL model except it is for a ternary mixture of solvent (1), solvent (2), and polymer (3). A concentration-dependent self-diffusivity is specified. The <species> is defined and the {float_list}, consisting of 12 parameters is identical to and can be specified in the exact same order as in the binary case; see FREE_VOL model above for input parameter list. |
TABLE <integer1> <character_string1> {LINEAR | BILINEAR} [integer2] [FILE = filenm] |
Please see discussion at the beginning of the material properties Chapter 5 for input description and options. Most likely character_string1 will be MASS_FRACTION or TEMPERATURE. |
For the HYDRODYNAMIC flux model (Diffusion Constitutive Equation), there is only one valid choice for the Diffusivity {model_name}, i.e., HYDRO. There are no accompanying parameters but several additional cards are required to define different portions of the model; these cards are identified below. The user is referred to each individual card (identified by italic typeset) definition for the associated model choices and parameter lists.
HYDRO |
For mass transport driven by the hydrodynamic field. No <species> or {float_list} is required, although five additional input cards are required with this diffusivity model. The first specifies Dc in the Shear Rate Diffusivity card. The second specifies Dμ in the Viscosity Diffusivity card. The third specifies Dr in the Curvature Diffusivity card. The fourth specifies the diffusivity of a purely Fickian diffusion mode in the Fickian Diffusivity card; it is usually set to zero. The last card specifies Dg, in the Gravity-based Diffusivity card for the flotation term in variable density transport problems. |
ARRHENIUS <integer 1 <integer 2> <float1> <float2> <float3> |
This is a model for describing effect of temperature on Stefan-Maxwell diffusivities for application in modeling thermal batteries and thus it is used in conjunction with the STEFAN_MAXWELL_CHARGED or STEFAN_MAXWELL flux model (Diffusion Constitutive Equation). Two integers and three floats are required for this diffusivity model:
|
For the FICKIAN_CHARGED flux model (Diffusion Constitutive Equation), only constant diffusivities are allowed. So the Diffusivity model option is:
CONSTANT <species> <float1> |
a constant diffusivity model
|
In addition, the Charge Number and Solution Temperature cards must also be specified in the material file so that the migration flux may be calculated.
The STEFAN_MAXWELL and STEFAN_MAXWELL_CHARGED flux models (Diffusion Constitutive Equation) should be used to model the transport of two or more species only. The diffusivity model for species in these transport problems is currently limited to being CONSTANT and ARRHENIUS. In the CONSTANT& Stefan- Maxwell diffusivity model, a set (only n(n-1)/2 values since Dij = Dji and Dii are not defined) of diffusivities, Dij, is required:
CONSTANT <species> <float1> |
a constant diffusivity model
|
In addition, the Charge Number, Molecular Weight and Solution Temperature cards must also be specified in the material file so that the migration flux may be calculated.
Examples¶
Sections of material input files are shown below for several of the Diffusivity model options presented above.
Following is a sample input card for the CONSTANT Diffusivity model:
Diffusivity = CONSTANT 0 1.
Following is a sample section of the material file for the HYDRO Diffusivity model:
Diffusion Constitutive Equation = HYDRODYNAMIC
Diffusivity = HYDRO 0
Shear Rate Diffusivity = LINEAR 0 6.0313e-5
Viscosity Diffusivity = LINEAR 0 6.0313e-5
Curvature Diffusivity = CONSTANT 0 -48.02e-6
Fickian Diffusivity = ANISOTROPIC 0 0. 0.1e-5 0.
Gravity-based Diffusivity = RZBISECTION 0 2.14e-5 5.1 0.5 0.5
Following is a sample section of the material file for the GENERALIZED_FREE_VOL Diffusivity model:
Diffusion Constitutive Equation = GENERALIZED_FICKIAN
Diffusivity = GENERALIZED_FREE_VOL 1 0.943 1.004 0.000983 0.000239 -12.12 -96.4 0.395 0.266 0.00143 0 1.265983036 0.9233610342
Sample section of the material file for the STEFAN_MAXWELL_CHARGED Diffusion Constitutive Equation with the CONSTANT Diffusivity model:
Diffusion Constitutive Equation = STEFAN_MAXWELL_CHARGED
Diffusivity = CONSTANT
0 1 2.0e-05
0 2 2.0e-05
1 2 2.0e-05
Solution Temperature = THERMAL_BATTERY 846. 298. .03 7.7 0.6 1030.
Molecular Weight = CONSTANT 0 6.939
Charge Number = CONSTANT 0 1.0
Molecular Weight = CONSTANT 1 39.098
Charge Number = CONSTANT 1 1.0
Molecular Weight = CONSTANT 2 35.4
Charge Number = CONSTANT 2 -1.0
Sample section of the material file for the STEFAN_MAXWELL_CHARGED Diffusion Constitutive Equation with the ARRHENIUS Diffusivity model:
0 1 1.5e-05 80000.0 846.0
0 2 1.5e-05 80000.0 846.0
1 2 1.5e-05 80000.0 846.0
(the Charge Number, Molecular Weight and Solution Temperature cards are similarly specified as above in the CONSANT Diffusivity case)
Technical Discussion¶
Following are brief comments on the various Diffusivity models.
POROUS For this model, diffusivity depends on the saturation and porosity in a porous medium. For two-phase or unsaturated flow in a porous medium, the diffusivity calculated by this model is the diffusivity of solvent vapor through the gas phase in the pore-space (see Martinez, 1995). However as indicated above, this model is not recommended for use at his time.
GENERALIZED This model generalizes Fick’s Law for multicomponent diffusion. The elements along the diagonal, Dii, are self-diffusivities, while Dij are mutual diffusivities between species i and j. Note that mutual diffusivities in generalized formulation can be both positive and negative, and are constant values.
FREE_VOL For a diffusivity determined by free volume theory (cf. Duda et al. 1982). In mathematical form, the binary mutual diffusion coefficient (solvent diffusion in a polymeric solution), using the free volume theory, is given by:
where
Here, ω1 is the solvent weight fraction, ω2 polymer weight fraction; V0 1 and V02 are, respectively, solvent and polymer specific volumes; φ1 solvent volume fraction, φ2 polymer volume fraction; γ overlap factor to account for shared free volume; Tg1 and Tg2 respectively solvent and polymer glass transition temperature, T absolute temperature; K11, K12, K21 and K22 solvent free-volume parameters; V* 1 and V*2 respectively, solvent and polymer specific critical-hole volumes; D01 constant preexponential factor when E is presumed to be zero (E is energy required to overcome attractive forces from neighboring molecules); ξ ratio of solvent and polymer jumping units; and χ Flory-Huggins polymer/solvent interaction parameter. In general, D01 should be expressed as D01 e- E/RT with R being the universal gas constant. Dependence of diffusivity, D, on temperature and mass fraction can be determined once the above twelve parameters are specified.
Note: This model (FREE_VOL) can be run ONLY with 1 species equation, i.e., with two components.
GENERALIZED_FREE_VOL This is a diffusivity model based on free volume theory and the generalized Fick’s law. For a ternary mixture of solvent (1), solvent (2), and polymer (3), the concentration-dependent self-diffusivity is given by (Vrentas, et. al., 1984):
where
The parameters for this model are the same twelve parameters as for the binary FREE_VOL model and so can be specified in the exact same order. The mutual diffusivities required to fill the cross-terms are also concentration-dependent. In addition, the gradient in chemical potential is also accounted for (Alsoy and Duda, 1999; Zielinski and Hanley, 1999).
ai is the activity of species i, which can be written in terms of the activity coefficient, γi, and volume fraction, φi. The current implementation of species activity is based on the Flory-Huggins model for multicomponent polymer-solvent mixtures (Flory, 1953).
HYDRO implies that mass transport of at least one species is driven by gradients in the second invariant of the rate of deformation tensor (shear rate) and gradients in viscosity (Phillips, et.al. 1992). This model also includes a sedimentation flux term to account for the motion of non-neutrally buoyant particles resulting from gravitation (Zhang and Acrivos, 1994) and a curvature-driven flux term from normal component of the acceleration vector (Krishnan, et. al., 1996). This model is used in predicting the particle distributions of particulate suspensions undergoing flow. For this model, the mass flux vector J is given by the following:
where
where Ci is the particulate phase volume fraction, i is the species number designation of the particulate phase, the shear rate, μ the viscosity, the normal unit acceleration vector, r the curvature of streamlines, Dc, Dμ, Dr and Dg the “diffusivity” parameters, ρs and ρf the particle and fluid phase densities, respectively, and , the gravitational acceleration vector.
ARRHENIUS Diffusivities can be strongly dependent on temperature as in processes such as thermal batteries. Such temperature dependency can be described using the following constitutive model that makes use of Arrhenius temperature dependency:
where Dij are the Stefan-Maxwell diffusivities as defined in Equations 13 and 14. are the reference Stefan-Maxwell diffusivities at reference temperature T0; ED is the activation energy that controls the temperature dependency and R is the universal gas constant; and T is temperature. The units of ED, R and T are such that is dimensionless.
STEFAN-MAXWELL For multicomponent diffusion of neutral species in concentrated solutions. The Stefan-Maxwell diffusivities, Dij, as defined in the following Stefan-Maxwell flux model (cf. Chen, et. al., 2000, Chen, et. al., 1998):
are taken to be constant. Here, xi is mole fraction of species i, Ji the molar flux of species i, and c the total molar concentration. Since Dij = Dji and Dii are not defined, only n(n-1)/2 Stefan-Maxwell diffusivities are required (here, n is the total number of diffusing species). For example, for n = 3 (i.e., a solution having three species), three Stefan-Maxwell diffusivities are needed: D12, D13, and D23.
STEFAN-MAXWELL_CHARGED For multicomponent transport (diffusion and migration) of charged species in concentrated electrolyte solutions. The Stefan- Maxwell diffusivities, Dij, as defined in the following Stefan-Maxwell flux model (cf. Chen et al. 2002, Chen, et. al., 2000, Chen, et. al., 1998):
are taken to be constant, as in the case of multicomponent diffusion of neutral species in concentrated solutions. Here, Φ is electrical potential in electrolyte solution, zi charge number of species i, F Faraday constant (96487 C/mole), R universal gas constant (8.314 J/mole-K), and T electrolyte solution temperature.
FICKIAN_CHARGED For multicomponent transport (diffusion and migration) of charged species in dilute electrolyte solutions. The Fickian diffusivity of species i, Di, as defined in the following Fickian flux model (cf. Newman, 1991; Chen, et. al., 2000):
is taken to be constant. Here, ci is molar concentration of species i.
FAQs¶
The following is a discussion of Units in Goma but covers several important Diffusionrelated items. It comes from some emails exchanged at Sandia during January 1998; while the discussions are relevant for each user of the code, the deficiencies or lack ofclarity have been since been remedied prior to Goma 4.0.
Unit Consistency in Goma (Jan 98)
Question:… I know what you are calling volume flux is mass flux divided by density. The point I am trying to make is that the conservation equations in the books I am familiar with talk about mass, energy, momentum, and heat fluxes. Why do you not write your conservation equations in their naturally occurring form? If density just so happens to be common in all of the terms, then it will be obvious to the user that the problem does not depend on density. You get the same answer no matter whether you input rho=1.0 or rho=6.9834, provided of course this does not impact iterative convergence. This way, you write fluxes in terms of gradients with the transport properties (viscosity, thermal conductivity, diffusion coefficient, etc.) being in familiar units.
Answer: First let me state the only error in the manual that exists with regard to the convection-diffusion equation (CDE) is the following:
Ji in the nomenclature table should be described as a volume flux with units of L/t, i.e. D ⋅ ∇yi, where D is in L2/t units.
Now, this is actually stated correctly elsewhere, as it states the Ji is a diffusion flux (without being specific); to be more specific here, we should say it is a “volume flux of species i.” So, in this case D is in L ⋅ L ⁄ t units, yi is dimensionless and it is immaterial that the CDE is multiplied by density or not, as long as density is constant.
Now, in Goma we actually code it with no densities anywhere for the FICKIAN diffusion model. For the HYDRO diffusion model, we actually compute a Ji ⁄ ρ in the code, and handle variable density changes through that . In that case Ji as computed in Goma is a mass flux vector, not a volume flux vector, but by dividing it by and sending it back up to the CDE it changes back into a volume flux. i. e., everything is the same.
Concerning the units of the mass transfer coefficient on the YFLUX boundary condition, the above discussion now sets those. Goma clearly needs the flux in the following form:
and dimensionally for the left hand side
where D is in units L2 ⁄ t, the gradient operator has units of 1 ⁄ L so K has to be in units of L ⁄ t (period!) because yi is a fraction.
then K’s units will have to accommodate for the relationship between p1 and y1 in the liquid, hopefully a linear one as in Raoult’s law, i.e. if pi = PVyi where pv is the vapor pressure, then
and so K on the YFLUX command has to be KPv ….and so on.
Finally, you will note, since we do not multiply through by density, you will have to take care of that, i. e., in the Price paper (viz., Price, et. al., 1997) he gives K in units of t ⁄ L. So, that must be converted as follows:
This checks out!
References¶
Alsoy, S. and Duda, J. L., 1999. “Modeling of Multicomponent Drying of Polymer Films.” AIChE Journal, (45)4, 896-905.
Chen, K. S., Evans, G. H., Larson, R. S., Noble, D. R. and Houf, W. G. “Final Report on LDRD Project: A Phenomenological Model for Multicomponent Transport with Simultaneous Electrochemical Reactions in Concentrated Solutions”, SAND2000- 0207, Sandia National Laboratories Technical Report (2000).
Chen, K. S., Evans, G. H., Larson, R. S., Coltrin, M. E. and Newman, J. “Multidimensional modeling of thermal batteries using the Stefan-Maxwell formulation and the finite-element method”, in Electrochemical Society Proceedings, Volume 98-15, p. 138-149 (1998).
Chen, K. S., “Modeling diffusion and migration transport of charged species in dilute electrolyte solutions: GOMA implementation and sample computed predictions from a case study of electroplating”, Sandia memorandum, September 21, 2000.
Chen, K. S., Evans, G. H., and Larson, R. S., “First-principle-based finite-element modeling of a Li(Si)/LiCl-KCl/FeS2 thermal battery cell”, in Electrochem. Soc. Proc. Vol. 2002-30, p. 100 (2002).
Duda, J. L., Vrentas, J. S., Ju, S. T. and Liu, H. T. 1982. “Prediction of Diffusion Coefficients for Polymer-Solvent Systems”, AIChE Journal, 28(2), 279-284.
P.J. Flory, Principles of Polymer Chemistry, Cornell University Press, 1953. Krishnan, G. P., S. Beimfohr and D. Leighton, 1996. “Shear-induced radial segregation in bidisperse suspensions,” J. Fluid Mech. 321, 371.
Martinez, M. M., Mathematical and Numerical Formulation of Nonisothermal Multicomponent Three-Phase Flow in Porous Media, SAND95-1247, Sandia National Laboratories Technical Report, 1995.
Newman, J. S., Electrochemical Systems, Prentice Hall, Inc., Englewood Cliffs, New Jersey (1991).
Phillips, R.J., R.C. Armstrong and R.A. Brown, 1992, “A constitutive equation for concentrated suspensions that accounts for shear-induced particle migration,” Physics of Fluids A, 4(1), 30-40.
Price, P. E., Jr., S. Wang, I. H. Romdhane, “Extracting Effective Diffusion Parameters from Drying Experiments,” AIChE Journal, 43, 8, 1925-1934 (1997)
Vrentas, J.S., J.L. Duda and H.-C. Ling, 1984. “Self-Diffusion in Polymer-Solvent- Solvent Systems” Journal of Polymer Sciences: Polymer Physics edition, (22), 459- 469.
Zhang K. and A. Acrivos, 1994, “Viscous resuspension in fully-developed laminar pipe flows,” Int. J. Multiphase Flow, (20)3, 579-591.
Zielinski, J.M. and B.F. Hanley, 1999. “Practical Friction-Based Approach to Modeling Multicomponent Diffusion.” AIChE Journal, (45)1, 1-12.
Shear Rate Diffusivity¶
Shear Rate Diffusivity = {model_name} <species> <float>
Description / Usage¶
This card is used to specify the coefficient for the shear-rate gradient term when HYDRO is specified in the Diffusivity card. Definitions of the input parameters follow for the {model_name} options CONSTANT and LINEAR based on the model:
CONSTANT |
Name of the model for constant shear rate diffusivity.
|
LINEAR |
Name of the model in which shear rate diffusivity is a linear function of concentration.
|
Technical Discussion¶
Please refer to the technical discussion given under HYDRO section of the Diffusivity card.
References¶
No References.
Viscosity Diffusivity¶
Viscosity Diffusivity = {model_name} <species> <float>
Description / Usage¶
This card is used to specify Dr when the model in the Diffusivity card is HYDRO. Definitions of the input parameters follow for the {model_name} options CONSTANT and LINEAR based on the model:
CONSTANT |
Name of the model for a constant curvature diffusivity.
|
LINEAR |
Name of the model in which the diffusivity is a linear function of concentration.
|
Technical Discussion¶
Please refer to the technical discussion given under HYDRO section of the Diffusivity card.
References¶
No References.
Curvature Diffusivity¶
Curvature Diffusivity = {model_name} <species> <float>
Description / Usage¶
This card is used to specify Dr when the model in the Diffusivity card is HYDRO. Definitions of the input parameters follow for the {model_name} options CONSTANT and LINEAR based on the model:
CONSTANT |
Name of the model for a constant curvature diffusivity.
|
LINEAR |
Name of the model in which the diffusivity is a linear function of concentration.
|
Technical Discussion¶
It was proposed that adding a curvature contribution of the diffusive flux for suspension particles would correct suspension migration behavior in parallel-plate and cone-and-plate. However, this correction term is not frame-invariant; hence, it cannot be used in generalized flow geometry. It is therefore not recommended.
References¶
No References.
Fickian Diffusivity¶
Fickian Diffusivity = {model_name} <species> {float_list}
Description / Usage¶
This card allows the user to select a Fickian diffusion mode when the model in the Diffusivity card is HYDRO. There are two {model_name} options for this mode; definitions of the input parameters are as follows:
ANISOTROPIC |
an anisotropic Fickian diffusion.
|
EXP_DECAY |
an exponential decay of flux.
|
Examples¶
Following are two sample cards:
Fickian Diffusivity = ANISOTROPIC 0 2.e-6 2.e-6 0.
Fickian Diffusivity = EXP_DECAY 0 0.01 1.e-3
Technical Discussion¶
In modeling suspension flow, often a sharp concentration gradient is encountered, and the numerical convergence becomes very poor. This card should be used for numerical stability (smooth out the wiggles) and should only be introduced as a last resort. The magnitudes should remain small relative to shear rate and viscosity diffusivities.
As the name implied, anisotropic Fickian diffusivity defines an additional flux contribution much like a classic Fickian diffusion term; i.e.,
If the exponential decay option is used, the flux vector has the form,
where C and Cmax are volume fractions of suspension locally and at maximum packing.
References¶
No References.
Gravity-based Diffusivity¶
Gravity-based Diffusivity = {model_name} <species> {float_list}
Description / Usage¶
This card is used to specify Dg when the model in the Diffusivity card is HYDRO. There are two {model_name} options for this mode; definitions of the input parameters are as follows:
CONSTANT |
constant gravity-based diffusivity.
|
RICHARDSON_ZAKI |
constant gravity-based diffusivity.
|
Examples¶
The following is a sample input card:
Gravity-based Diffusivity = CONSTANT 0 8.88e-7
Gravity-based Diffusivity = RICHARDSON_ZAKI 0 8.88e-7 5.1
Technical Discussion¶
When a suspension of particles settles or floats in a fluid, particle-particle interactions serve to slow the terminal velocity of all the particles relative to the Stokes velocity. The terminal velocity is then corrected by what is known as the hindered settling function. If a CONSTANT model is chosen, the form of this function is
where φ is the volume fraction of suspension, η(φ) is the relative viscosity of the mixture, μ0 is the viscosity of the pure fluid.
On the other hand if RICHARDSON_ZAKI is chosen for the function,
where n is the exponent specified by the user. n=5.1 has been found to fit well for suspensions of monodisperse spherical particles at low Reynolds number by Garside and Al-Dibouni (1977). Richardson-Zaki approach will not yield a zero f(φ) if φ approaches maximum packing, so it is recommended that CONSTANT is used.
References¶
GTM-010.0: The Hindered Settling Function for a Glass Microballoon Suspension, March 3, 1999, C. A. Romero.
Garside, J. and M.R. Al-Dibouni, “Velocity-voidage relationship for fluidization and sedimentation in solid-liquid systems,” Ind. Eng. Chem. Process Des. Dev., 16, 206 (1977).
Q Tensor Diffusivity¶
Q Tensor Diffusivity = <integer> <float_list>
Description / Usage¶
This card specifies the coefficients for use in the Q-tensor suspension rheology model. The <float_list> has three values, one for each direction, so the input parameters are defined as follows:
<integer> |
Species number for suspension volume fraction. |
<float1> |
Coefficient of eigenvectors in the flow direction. |
<float2> |
Coefficient of eigenvectors in the gradient direction. |
<float3> |
Coefficient of eigenvector in the vorticity direction. |
Examples¶
The current best selection of coefficients is given by:
Q Tensor Diffusivity = 0 1.0 1.0 0.5
Technical Discussion¶
The three directions (1, 2, 3) are often called the (flow, gradient, vorticity) directions. Here, vorticity is not curl(u), but defined (along with the other three) for a particular set of circumstances: steady simple shear flow. Their analogous definitions in other regimes, as well as the selection of the coefficients, is an active area of research. The interested reader should review the references listed below.
References¶
Brady, J. F. and Morris J. F., “Microstructure of strongly sheared suspensions and its impact on rheology and diffusion,” J. of Fluid Mechanics, v. 348 pp.103-139, Oct 10, 1997.
Fang, Z. W., Mammoli, A. A., Brady, J.F., Ingber, M.S., Mondy, L.A. and Graham, A.L., “Flow-aligned tensor models for suspension flows,” Int. J. of Multiphase Flow, v. 28(#1) pp. 137-166, January 2002.
Hopkins, M. M., Mondy, L. A., Rao, R. R., Altobelli, S. A., Fang, Z., Mammoli, A. A. and Ingber, M. S., 2001. “Three-Dimensional Modeling of Suspension Flows with a Flow-Aligned Tensor Model”, The 3rd Pacific Rim Conference on Rheology, July 8- 13, 2001, Vancouver, B.C., Canada.
Morris, J. F. and Boulay, F., “Curvilinear flows of noncolloidal suspensions: The role of normal stresses,” J. of Rheology, v. 43(#5) pp. 1213-1237 Sep-Oct 1999.
Species Time Integration¶
Species Time Integration= {model_name} <species>
Description / Usage¶
Sharp gradients are often a feature of convective-diffusive computations involving species. Traditional Galerkin time integration is not optimal under these circumstances. This optional card is used to change the species time integration scheme to be different from the global time integration. Each species equation can use a different time integration. The new time integration schemes are based upon a Taylor-Galerkin formulation which has better behavior when sharp fronts are present.
Following are the {model_name} options for species time integration, each of which requires only a species designation to which the model should be applied:
STANDARD |
the input deck formulation, i.e., the global time integration scheme; this is the default.
|
TAYLOR_GALERKIN |
an implicit or semi-implicit Taylor-Galerkin time integration scheme
|
TAYLOR_GALERKIN_EXP |
An explicit Taylor-Galerkin time integration scheme
|
Examples¶
The following sample input card invokes the explicit Taylor-Galerkin time integration of the species equation.
Species Time Integration = TAYLOR_GALERKIN_EXP 0
Technical Discussion¶
The Taylor-Galerkin schemes are designed for advection dominated problems with sharp fronts where rigorous mass conservation is important.
TAYLOR_GALERKIN uses an implicit or semi-implicit form of the Taylor- Galerkin time integrals depending on what is chosen in the input deck.
TAYLOR_GALERKIN_EXP uses an explicit form of the equations and is favored for volume-of-fluid simulations where the diffusive character of the implicit solver creates mass balance errors. The drawback of explicit time integration methods is that the time step used is governed by the Courant limit and must be quite small for stability.
References¶
No References.
Advective Scaling¶
Advective Scaling = {model_name} <species> <float>
Description / Usage¶
This material property card permits the user to scale only the advective terms in one or more of the species transport equations by a fixed constant. This may be useful when solving problems with non-standard concentrations or for stability reasons.
A single {model_name} is available; it and its parameters are described below:
CONSTANT |
Model used to specify the advective scaling.
|
Examples¶
Here is an example of the card:
Advective Scaling = CONSTANT 0 0.0
In this case, the card is being used to eliminate the advective terms in the conservation equation for species 0.
Technical Discussion¶
The advective terms in the species conservation equations take the form, u ⋅ ∇c where c is the species concentration and u the fluid velocity.
References¶
No References.
Latent Heat Vaporization¶
Latent Heat Vaporization = CONSTANT <species> <float> [E/M]
Description / Usage¶
This required card is used to specify the model for the latent heat of vaporization for each species. Definitions of the input parameters are as follows:
CONSTANT |
Name of the constant latent heat of vaporization model.
|
Technical Discussion¶
See the discussion for the Latent Heat Fusion model.
References¶
No References.
Latent Heat Fusion¶
Latent Heat Fusion = CONSTANT <species> <float> [E/M]
Description / Usage¶
This card is used to specify the model for the latent heat of fusion for each species. Thus an input deck may include several of these cards. Definitions of the input parameters are as follows:
CONSTANT |
Name of the latent heat of fusion model, the only one available.
|
Technical Discussion¶
This card is used on a species-basis and is unrelated to the latent heat of fusion specification for the ENTHALPY model of heat capacity. It is used to calculate the standard state heat of formation for the species. A related important card is the Latent Heat Vaporization.
References¶
No References.
Vapor Pressure¶
Vapor Pressure = {model_name} <species> {float_list} [varies]
Description / Usage¶
This required card is used to specify the model for the vapor pressure for each species; it has two main classes of use. The first class regards multiphase flow in porous media, which is activated when the media type is set to POROUS_UNSATURATED or TWO_PHASE (cf. the Media Type card). The second class of use of this data card is for specification of vapor pressure at the external boundary of a liquid domain, for which the bounding gas phase is modeled with a lumped parameter approach, or at an internal interface between a liquid and a gas. No curvature effects are included here. Eventually the models in this class will be supported in the porous-media cases. Definitions of the input parameters are as follows:
{model_name} |
Name of the model for the vapor pressure, based on the class of use. For the first class of multiphase flows in porous media, {model_name} can be one of the following:
For the second class regarding specification of vapor pressure at the external boundary of a liquid domain or the interface between a gas and a liquid, {model_name} can be one of the following:
|
<species> |
An integer designating the species equation. Typically this value is zero if the problem is one of a single solvent in a partially saturated medium. |
{float_list} |
One or more floating point numbers (<float1> through <floatn>) whose values are determined by the selection for {model_name}. |
Vapor pressure model choices and their parameters are discussed below.
Models in the first class…
KELVIN <species> <float_list> |
The <float_list> for the KELVIN option specifies input values for seven parameters:
The KELVIN option is used to include the effect of vapor-pressure lowering that results in equilibrium over high curvature menisci, i.e., small pores. The equation form of this is |
FLAT <species> <float_list> |
The FLAT option requires the same seven parameters as the KELVIN model but leaves off the exponential function, i.e., the vapor pressure is independent of the level of capillary pressure. The constants are still needed so that the gas-phase concentration can be calculated with the ideal gas law. See the KELVIN option above for definition of the <float_list> values. |
IDEAL_GAS <species> <float_list> |
The <float_list> for this model has three values, where:
|
Models in the second class..
CONSTANT <species> <float1> |
This model is used for a constant species source such as a homogeneous reaction term. The <float_list> has a single value:
|
ANTOINE <species> <float_list> |
The ANTOINE model for vapor pressure is used in conjunction with the VL_EQUIL boundary condition. If specified, a temperature-dependent vapor pressure for species i is calculated. The model requires six values in the <float_list>, where:
|
RIEDEL <species> <float_list> |
The RIEDEL model for vapor pressure is used in conjunction with the VL_EQUIL boundary condition card. If specified, a temperature-dependent vapor pressure for species i is calculated. The model requires eight values in the <float_list>, where:
|
Examples¶
An example use of the Antoine model for vapor pressure follows:
Vapor Pressure = ANTOINE 0 1 9.380340229 3096.516433 -53.668 0.1 1000
Technical Discussion¶
No Discussion.
References¶
No References.
Species Volume Expansion¶
Species Volume Expansion = CONSTANT <species> <float> [1/T]
Description / Usage¶
This card is used to specify the model for the coefficient of volume expansion associated with the concentration of a particular species. This property is optional for the BOUSS and BOUSSINESQ option on the Navier-Stokes Source card and, if nonzero, will result in a buoyancy term to be added to the Navier-Stokes equation that is apportioned to the species volume expansion coefficient, defined as the logarithmic sensitivity of density to concentration, or (dlnr) ⁄ (dC).
CONSTANT |
Name of the constant volume expansion coefficient model.
|
Technical Discussion¶
WARNING: Please be aware that if the thermal volume expansion coefficient is also nonzero, the buoyancy force will be augmented.
References¶
No References.
Standard State Chemical Potential¶
Standard State Chemical Potential = CONSTANT <integer> <float>
Description / Usage¶
This card sets the standard state chemical potential of a species, <integer>, in the current material to a specified value, <float>. Currently, only the generic CONSTANT model is implemented. However, extensions to polynomial expressions in the temperature are easily implemented and forthcoming.
CONSTANT |
Model name for the standard chemical state chemical potential model.
|
The standard state chemical potential, μk, o(T) , which is defined to be only a function of the temperature, is used in the evaluation of the definition of the pure species chemical potential of species k, μk (T, P) , which in turn is used in the evaluation of the mixture chemical potential of species k, μk(T, P, Xi) .
Technical Discussion¶
The values in this card are currently only applicable to the IS_EQUIL_PSEUDORXN boundary condition.
References¶
No References.
Pure Species Chemical Potential¶
Pure Species Chemical Potential = {model_name} <integer>
Description / Usage¶
This card takes the specification of the standard state chemical potential, which is defined as a function of temperature only, and completes the definition of the pure species chemical potential by possibly adding in a pressure dependence. Two model values are permissible:
PRESSURE_INDEPENDENCE |
No pressure dependence to the pure species state when this value of {model_name} is specified. The standard state chemical potential is equal to the pure species chemical potential. The <integer> argument specifies the species subindex, k. |
PRESSURE_IDEALGAS |
The following expression holds for the pressure dependence:
The standard state chemical potential, μk, o(T), which is defined to be only a function of the temperature, is used in the evaluation of the definition of the pure species chemical potential of species k, μk*(T, P) , which in turn is used in the evaluation of the mixture chemical potential of species k, μk (T P Xi). |
Technical Discussion¶
The values in this card are only applicable to the IS_EQUIL_PSEUDORXN boundary condition currently.
References¶
No References.
Chemical Potential¶
Chemical Potential = {IDEAL_SOLUTION | STOICHIOMETRIC_PHASE}
Description / Usage¶
This card is used to specify the formulation of the chemical potential for the phase. It is currently unconnected to Goma’s functionality. Two values are permissible:
IDEAL_SOLUTION |
Ideal solution thermodynamics |
STOICHIOMETRIC_PHASE |
Phase consists of fixed set of molecular composition |
Technical Discussion¶
The chemical potential of species k in an ideal solution is given by the expression, [Denbigh, p. 249],
where μk*(T, P) is defined as the chemical potential of species k in its pure state (or a hypothetical pure state if a real pure state doesn’t exist) at temperature T and pressure P. μk*(T, P) is related to the standard state of species k in the phase, μk, o(T), which is independent of pressure, through specification of the pressure dependence of the pure species k. Xk is the mole fraction of species k in the phase.
The chemical potential of species k (actually there is only one species!) in a stoichiometric phase is equal to
References¶
Denbigh, K., The Principles of Chemical Equilibrium, 4th Ed., Cambridge University Press, 1981
Reference Concentration¶
Reference Concentration = CONSTANT <species> <float> []
Description / Usage¶
This required card is used to specify the model for the reference concentration, which is required by the BOUSS option on the Navier-Stokes Source card. Definitions of the input parameters are as follows:
CONSTANT |
Model for a constant reference concentration.
|
Technical Discussion¶
The Boussinesq model subtracts out the pressure head in its final equations. Thus, to zeroth order, hydrodynamic pressure field doesn’t include a static variation in the gravity direction due to the pressure head. But, the source term in the momentum equations then becomes –g(ρ – ρo) instead of simply –gρ. The reference concentration values entered via this card are used to evaluate ρo for use in calculating the natural convective force due to concentration differences.
The card is also used in various places where a value for a species concentration is needed. However, the species unknown variable is not included in the solution vector.
References¶
No References.
Molecular Weight¶
Molecular Weight = CONSTANT <integer> <float>
Description / Usage¶
This card specifies the molecular weight of a species. It is required when the Stefan- Maxwell flux model is used in modeling multicomponent transport of neutral or charged species. It is also required when vapor-liquid phase equilibrium is considered at the material boundaries. Molecular weight is used to convert units of mass fraction to mole fraction in a species material balance.
CONSTANT |
Molecular weight model type.
|
Technical Discussion¶
This card originated from the development of a multicomponent diffusion model based on the Stefan-Maxwell equation. However, it has been generalized to include problems where mole fractions are necessary for the consideration of phase equilibria. For example, when YFLUX_EQUIL is invoked in the input deck, an equilibrium problem is solved rigorously which requires gas and liquid mole fractions. The conversion from mass fraction to mole fraction requires molecular weight information.
References¶
No References.
Specific Volume¶
Specific Volume = CONSTANT <integer> <float>
Description / Usage¶
This card specifies the specific volume of a species. It is required when polymersolvent vapor-liquid phase equilibrium is considered at the material boundaries. Specific volume is used to convert units of mass fraction to volume fraction in species material balance.
CONSTANT |
Specific volume model type.
|
Technical Discussion¶
This is the place where pure component density (inverse of specific volume) information is entered in the material property. When Flory-Huggins vapor-liquid equilibrium model was first developed in Goma, the equations were based on volume fractions, not mass fractions. In order to convert these units, the specific volume parameter is required for each component in the mixture.
This card is used only in conjunction with Flory-Huggins nonideal liquid activity model for polymer-solvent mixtures. This occurs when two types of BCs are specified: 1) when VL_POLY is specified at an discontinuous internal boundary and 2) when FLORY model under YFLUX_EQUIL boundary card is specified.
References¶
No References.
Molar Volume¶
Molar Volume = CONSTANT <integer> <float> [L3/mole]
Description / Usage¶
This card is referred when molar based equilibrium models are used on the boundaries, such as VL_POLY. The float value specified is necessary for converting mass fractions to mole fractions.
CONSTANT |
Model for converting mass to mole fractions.
|
Technical Discussion¶
The same conversion from mass fraction to mole fraction can be obtained through specification of the Molecular Weight and Specific Volume. The redundancy, which will be allowed to remain, arose through simultaneous additions to the code by developers working on different projects.
References¶
No References.
Charge Number¶
Charge Number = CONSTANT <integer> <float>
Description / Usage¶
This card is required when charged species are involved, e.g. when using the FICKIAN_CHARGED or the STEFAN_MAXWELL_CHARGED Diffusion Constitutive Equation card. It specifies the charge number (e.g., the charge number for Ni2+ is 2, and that for SO2-is -2) of a species.
CONSTANT |
Model for specifying constant charge on species.
|
Technical Discussion¶
No Discussion.
References¶
No References.
Non-condensable Molecular Weight¶
Non-condensable Molecular Weight = CONSTANT <integer> <float>
Description / Usage¶
This card specifies the molecular weight of a species when the species is implicit in the mixture. This means that in most problems involving n+1 species, only n species are independent; i.e.,
It is required when Flory-Huggins vapor-liquid phase equilibrium is considered at the material boundaries, as used in VL_POLY and in FLORY under YFLUX_EQUIL. This is used to convert units of mass fraction to mole fraction in species material balance.
CONSTANT |
Model for converting mass to mole fractions.
|
Examples¶
The following is an example card:
Non-condensable Molecular Weight = CONSTANT 2 36.
This example shows that two species are solved in the Goma problem explicitly: species 0 and species 1.
Technical Discussion¶
In the current set up, species balance in Goma considers the species to be independent of each other. However, the mass or volume fractions of all species must add up to unity in any mixtures. This means that some properties of the last species must be entered in the material file although that component is not solved explicitly in the problem. This is the case for molecular weight, molar volume, and specific volume specifications, which are required for calculating Flory-Huggins liquid activity.
References¶
No References.
Non-volatile Molar Volume¶
Non-volatile Molar Volume = CONSTANT <integer> <float>
Description / Usage¶
This card specifies the molar volume of a species when the species is implicit in the mixture. This means that in most problems involving n+1 species, only n species are independent; i.e.,
IIt is required when Flory-Huggins vapor-liquid phase equilibrium is considered at the material boundaries, as used in VL_POLY and in FLORY under YFLUX_EQUIL. This is used to convert units of mass fraction to mole fraction in species material balance.
CONSTANT |
Model for converting mass to mole fractions.
|
Examples¶
The following is an example card:
Non-volatile Molar Volume = CONSTANT 2 1.5e-3
This example shows that two species are solved in the Goma problem explicitly: species 0 and species 1.
Technical Discussion¶
In the current set up, species balance in Goma considers the species to be independent of each other. However, the mass or volume fractions of all species must add up to unity in any mixtures. This means that some properties of the last species must be entered in the material file although that component is not solved explicitly in the problem. This is the case for molecular weight, molar volume, and specific volume specifications, which are required to calculate Flory-Huggins liquid activity.
References¶
No References.
Non-volatile Specific Volume¶
Non-volatile Specific Volume = CONSTANT <integer> <float>
Description / Usage¶
This card specifies the specific volume of a species when the species is implicit in the mixture. This means that in most problems involving n+1 species, only n species are independent; i.e.,
It is required when Flory-Huggins vapor-liquid phase equilibrium is considered at the material boundaries, as used in VL_POLY and in FLORY under FLUX_EQUIL. This is used to convert units of mass fraction to mole fraction in species material balance.
CONSTANT |
Model for converting mass to mole fractions.
|
Examples¶
The following is an example card:
Non-volatile Specific Volume = CONSTANT 2 0.855e-3
This example shows that two species are solved in the Goma problem explicitly: species 0 and species 1.
Technical Discussion¶
In the current set up, species balance in Goma considers the species to be independent of each other. However, the mass or volume fractions of all species must add up to unity in any mixtures. This means that some properties of the last species must be entered in the material file although that component is not solved explicitly in the problem. This is the case for molecular weight, molar volume, and specific volume specifications, which are required for calculating Flory-Huggins liquid activity.
References¶
No References.
Flory-Huggins parameters¶
Flory-Huggins parameters = CONSTANT <integer1> <integer2> <float>
Description / Usage¶
This card specifies the Flory-Huggins binary interaction parameters. It is assumed that the binary parameters are symmetric; i.e.,
Therefore, one set of i-j coefficients is sufficient to describe the binary interaction coefficients.
CONSTANT |
Model for constant Flory-Huggins parameters.
|
Examples¶
Following is an example set of cards for a three-species mixture:
Flory-Huggins parameters = CONSTANT 0 1 0.3
Flory-Huggins parameters = CONSTANT 0 2 0.3
Flory-Huggins parameters = CONSTANT 1 2 0.3
This example shows that two species are solved in the Goma problem explicitly: species 0 and species 1.
Technical Discussion¶
No discussion; see Sun (1998).
References¶
GTM-007.1: New Multicomponent Vapor-Liquid Equilibrium Capabilities in GOMA, December 10, 1998, A. C. Sun